Скалярное произведение векторов. Условие ортогональности двух векторов
Определение
Скалярным произведением векторов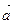 
и 
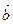называется число, равное произведению длин этих векторов на косинус угла 
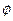между ними. Обозначается скалярное произведение так: 
, 
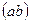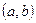или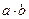 
. Итак
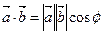 | (2.2.1) |
Поскольку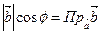 
(см. рис. 2.2.1), то получаем:
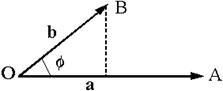
Рис. 2.2.1
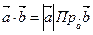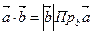 ,  . | (2.2.2) |
Если известны координаты перемножаемых векторов, т.е.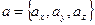 
, 
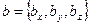, то скалярное произведение этих векторов можно вычислить по формуле:
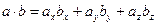 . | (2.2.3) |
Свойства скалярного произведения:
1. 
.
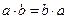2. 
.
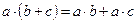3. 
.
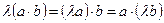4. Векторы 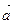и 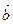взаимно перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю:
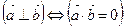 . | (2.2.4) |
5. Скалярный квадрат вектора равен квадрату его длины:
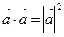 . | (2.2.5) |
Пример
Даны вершины треугольника A(–1,–2,4), B(–4,–2,0), C(3,–2,1). Определить его внутренний угол при вершине B.
Решение
Внутренний угол при вершине B (рис. 2.2.2) – это угол между векторам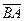и 
и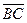 
: 
.
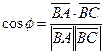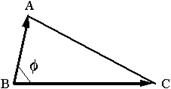
Рис. 2.2.2
Найдем координаты векторов 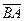и :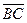 
; 
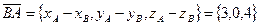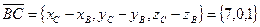. Скалярное произведение этих векторов и их длины:
,
,
.
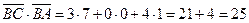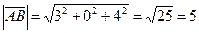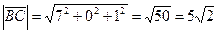Итак
.
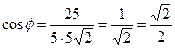
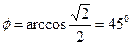Пример
Даны три вектора: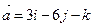 
, 
, 
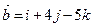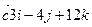. Найти 
.
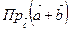Решение:
Векторы заданы их разложением по базису. Выпишем их координаты: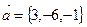 
, 
, 
, 
.
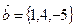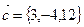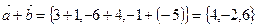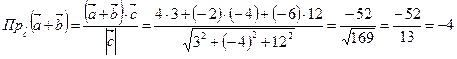
Знак “минус” говорит о том, что угол между векторам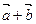и 
и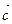 
тупой.
Пример
Определить при каком значении m векторы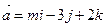 
и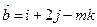 
взаимно перпендикулярны.
Решение
, 
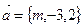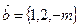. Векторы взаимно перпендикулярны, если их скалярное произведение равно нулю: 
; 
; 
.
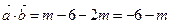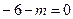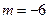Векторное произведение векторов. Условие коллинеарности двух векторов
Определение
Векторным произведением вектора 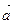на вектор 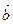называется вектор 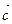, который определяется следующим образом:
1. Длина вектора 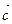равна произведению длин перемножаемых векторов на синус угла между ними:
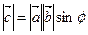 . | (2.3.1) |
2. Вектор 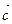перпендикулярен обоим перемножаемым векторам:
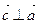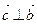 ,  . | (2.3.2) |
3. Направление вектора 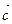таково, что, если смотреть из его конца вдоль вектора, то поворот на наименьший угол от первого сомножителя 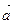ко второму сомножителю 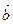виден совершающимся против движения часовой стрелки (рис. 2.3.1).
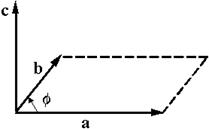
Рис. 2.3.1
Обозначается векторное произведение так: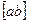 
, 
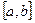или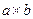 
. Если известны координаты перемножаемых векторов, т.е. 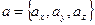, , 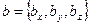то их векторное произведение можно найти по формуле:
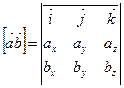 | (2.3.3) |
Пример
Найти векторное произведение векторов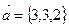 
, 
.
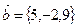Решение
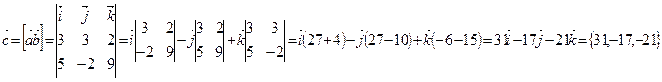
Основные свойства векторного произведения:
1. 
.
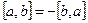2. 
.
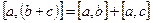3. 
.
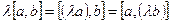4. 
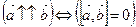
5. 
.
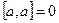Пример
Даны вершины треугольника A(1,2,0), B(3,0,–3), C(5,2,6). Вычислить его площадь.
Решение:
Треугольник ABC можно рассматривать построенным на векторах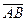 
и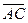 
(рис. 2.3.2).
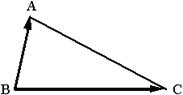
Рис. 2.3.2
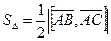Найдем координаты векторов 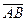и .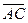 
; 
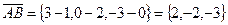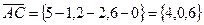. Вычислим векторное произведение этих векторов:
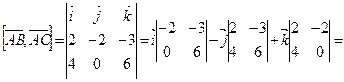
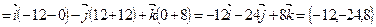
Находим длину вектора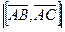 
:
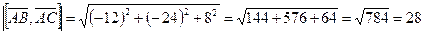
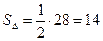
Пример
Сила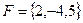 
приложена к точке A(4,–2,3). Найти момент этой силы относительно точки O(3,2,–1).
Решение
По определению момент силы есть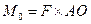 
. 
.
.
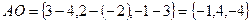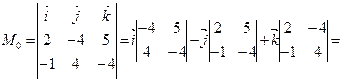
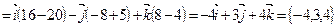Смешанное произведение векторов. Условие компланарности трех векторов
Определение
Смешанным произведением трех векторов 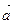, 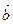и 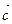называется произведение, составленное следующим образом: 
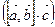, т.е. два вектора 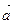и 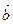умножаются векторно, а затем полученный вектор 
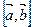скалярно умножается на третий вектор 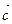. Смешанное произведение – это число.
Если известны координаты перемножаемых векторов , ,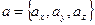 
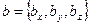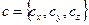, то их смешанное произведение можно вычислить по формуле:
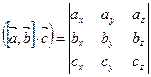 . | (2.4.1) |
С геометрической точки зрения смешанное произведение векторов 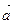, 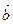и 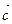с точностью до знака равно объему параллелепипеда, построенного на этих векторах, как на ребрах (рис. 2.4.1).
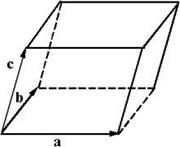
Рис. 2.4.1
Пример
Вычислить объем треугольной пирамиды, построенной на векторах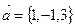 
, 
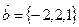и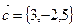 
.
Решение
Вычислим смешанное произведение векторов:
.
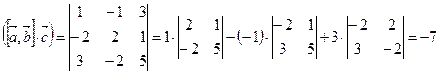
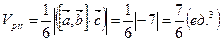Пример
Выяснить, лежат ли точки A(1,2,–1), B(0,1,5), C(–1,2,1) и D(2,1,3) в одной плоскости.
Решение:
Очевидно, точки A, B и C лежат в одной плоскости, если векторы 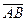, 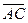и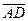 
компланарны.
Условием компланарности трех векторов является равенство нулю их смешанного произведения.
Найдем компоненты векторов: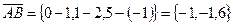 
; 
; 
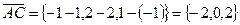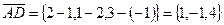. Вычислим смешанное произведение:
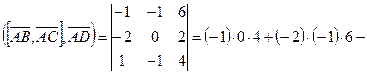
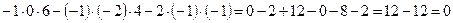
Так как смешанное произведение равно нулю, то вектора компланарны, а значит точки A, B, C и D лежат в одной плоскости.