Балльно-рейтинговая карта дисциплины. Кафедра математики и методики обучения
ПОВОЛЖСКАЯ ГОСУДАРСТВЕННАЯ СОЦИАЛЬНО-ГУМАНИТАРНАЯ АКАДЕМИЯ
Кафедра математики и методики обучения
Утверждено
на заседании кафедры
Протокол №
« » ____________ 2012 г.
Балльно-рейтинговая карта дисциплины
«Математический анализ»
Факультет математики, физики и информатики. Направления – «Математика» и «Информатика».
Курс 1 Семестр 1
Ведущий преподаватель:
к.ф.-м.н., доцент Барова Е.А.
Самара, 2012
| Вид контроля | Минимальное количество баллов | Максимальное количество баллов | |
| Модуль 1. Введение в анализ | |||
| Текущий контроль по модулю: | |||
| Аудиторная работа: | |||
| Самостоятельная работа № 1 «Область существования функции» | |||
| Самостоятельная работа № 2 «Вычисление пределов рациональных функций» | |||
| Самостоятельная работа № 2 «Вычисление пределов иррациональных функций» | |||
| Самостоятельная работа (домашняя) – альбом кривых | |||
| Контрольное мероприятие по модулю: | |||
| Теоретическая часть (коллоквиум) | |||
| Практическая часть (контрольная работа) | |||
| Промежуточный контроль | |||
| Модуль 2. Пределы трансцендентных функций | |||
| Текущий контроль по модулю: | |||
| Аудиторная работа: | |||
| Самостоятельная работа № 1 «Вычисление пределов тригонометрических функций» | |||
| Самостоятельная работа № 2 «Вычисление пределов показательно-степенных функций» | |||
| Контрольное мероприятие по модулю: | |||
| Теоретическая часть (коллоквиум) | |||
| Практическая часть (контрольная работа) | |||
| Промежуточный контроль | |||
| Промежуточная аттестация |
Преподаватель Барова Е.А., к.ф.-м.н., доцент кафедры математики и методики обучения
| Вид контроля | Примеры заданий, критерии оценки и количество баллов | Темы для изучения и образовательные результаты | |||||||||||||
| Модуль 1. Введение в анализ | |||||||||||||||
| Аудиторная работа | |||||||||||||||
| Самостоятельная работа № 1 «Область существования функции» | Примеры заданий.Уметь находить область определения функции, заданной аналитически. Например: 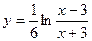 . Критерий оценки: 2 балла – пример решен правильно, 1 балл – пример решен с незначительными ошибками, 0 баллов – пример не решен. . Критерий оценки: 2 балла – пример решен правильно, 1 балл – пример решен с незначительными ошибками, 0 баллов – пример не решен. | Понятие функции. Область определения функции. | |||||||||||||
| Самостоятельная работа № 2 «Вычисление пределов рациональных функций» | Примеры заданий.Уметь вычислять пределы рациональных функций при 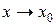 и и 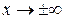 . Например, . Например, 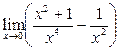 . Критерий оценки: 2 балла – пример решен правильно, 1 балл – пример решен с незначительными ошибками, 0 баллов – пример не решен. . Критерий оценки: 2 балла – пример решен правильно, 1 балл – пример решен с незначительными ошибками, 0 баллов – пример не решен. | Теоремы о пределе суммы, разности, произведения, частного. Теоремы о бесконечно больших и бесконечно малых функциях. Неопределенности вида 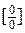 , , 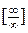 . . | |||||||||||||
| Самостоятельная работа № 3 «Вычисление пределов иррациональных функций» | Примеры заданий.Уметь вычислять пределы иррациональных функций при 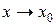 . Например, . Например, 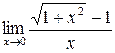 . Критерий оценки: 2 балла – пример решен правильно, 1 балл – пример решен с незначительными ошибками, 0 баллов – пример не решен. . Критерий оценки: 2 балла – пример решен правильно, 1 балл – пример решен с незначительными ошибками, 0 баллов – пример не решен. | Теоремы о пределе суммы, разности, произведения, частного. Теоремы о бесконечно больших и бесконечно малых функциях. Неопределенности вида 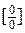 , , 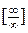 , , 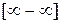 . . | |||||||||||||
| Самостоятельная работа (домашняя) – альбом кривых | Построить графики функций (с указанием области определения и множества значений) в «альбоме кривых»: 1) 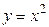 , , 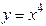 (на одном чертеже); 2) (на одном чертеже); 2) 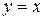 , , 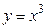 , , 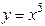 (на одном чертеже); 3) (на одном чертеже); 3) 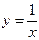 , , 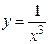 (на одном чертеже); 4) (на одном чертеже); 4) 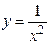 , , 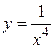 (на одном чертеже); 5) (на одном чертеже); 5) 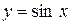 ; 6) ; 6) 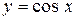 ; 7) ; 7) 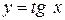 ; 8) ; 8) 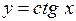 ; 9) ; 9) 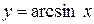 ; 10) ; 10) 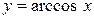 ; 11) ; 11) 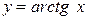 ; 12) ; 12) 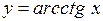 ; 13) ; 13) 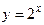 , , 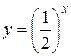 (на одном чертеже); 14) (на одном чертеже); 14) 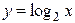 , , 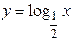 (на одном чертеже); Критерий оценки: 4 балла – все графики построены точно, область определения и множество значений каждой функции приведены верно 3 балла – графики 10 функций построены точно, область определения и множество значений каждой функции приведены верно 2 балла – графики 7 функций построены точно, область определения и множество значений каждой функции приведены верно 1 балл – имеются неточности более чем в 7 графиках функций и ошибки в области определения и множеств значений 0 баллов – не выполнен ни одиниз вышеперечисленных пунктов (на одном чертеже); Критерий оценки: 4 балла – все графики построены точно, область определения и множество значений каждой функции приведены верно 3 балла – графики 10 функций построены точно, область определения и множество значений каждой функции приведены верно 2 балла – графики 7 функций построены точно, область определения и множество значений каждой функции приведены верно 1 балл – имеются неточности более чем в 7 графиках функций и ошибки в области определения и множеств значений 0 баллов – не выполнен ни одиниз вышеперечисленных пунктов | Понятие функции. Область определения функции. Множество значений функции. | |||||||||||||
| Контрольное мероприятие по модулю | |||||||||||||||
| Теоретическая часть (коллоквиум) | Перечень вопросов. 1. Понятие множества. Основные числовые множества. Числовая прямая. Основные числовые множества: отрезок, интервал, полуинтервал. Абсолютная величина действительного числа и её свойства. Окрестность точки. 2. Действительная функция действительного переменного. График функции. Множество значений функции. Способы задания функции. Классификация основных элементарных функций. 3. Общие свойства функции: ограниченность функции, монотонность функции, четность-нечетность функции. На все свойства привести примеры. 4. Числовая последовательность. Определение конечного предела последовательности, его геометрический смысл. Используя определение предела последовательности, что 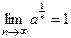 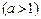 . 5. Бесконечные пределы последовательности. Доказать, используя определение бесконечного предела последовательности, что . 5. Бесконечные пределы последовательности. Доказать, используя определение бесконечного предела последовательности, что 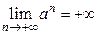 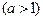 . 6. Теорема о единственности предела последовательности; теорема существования предела последовательности. 7. Понятие предела функции, его геометрический смысл. Доказать пределы: . 6. Теорема о единственности предела последовательности; теорема существования предела последовательности. 7. Понятие предела функции, его геометрический смысл. Доказать пределы: 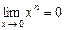 , , 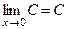 , , 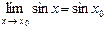 , , 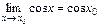 . Теорема об ограниченности функции, имеющей конечный предел. 8. Понятие бесконечно малых функций. Пример. Теоремы о бесконечно малых функциях. 9. Теоремы о пределе суммы, произведения, частного. Пределы элементарных функций. 10. 8 определений пределов функции с геометрической иллюстрацией. 11. Бесконечно большие функции. Теоремы о бесконечно больших функциях. Критерий оценивания. . Теорема об ограниченности функции, имеющей конечный предел. 8. Понятие бесконечно малых функций. Пример. Теоремы о бесконечно малых функциях. 9. Теоремы о пределе суммы, произведения, частного. Пределы элементарных функций. 10. 8 определений пределов функции с геометрической иллюстрацией. 11. Бесконечно большие функции. Теоремы о бесконечно больших функциях. Критерий оценивания.
| ||||||||||||||
| Практическая часть (контрольная работа) | Примеры заданий. 1. Найти область определения функций: а) 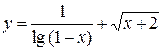 , б) , б) 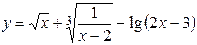 . 2. Вычислить пределы функций, формулируя используемые теоремы о пределах: а) . 2. Вычислить пределы функций, формулируя используемые теоремы о пределах: а) 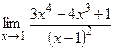 , б) , б) 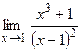 , в) , в) 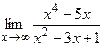 , г) , г) 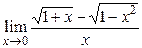 , д) , д) 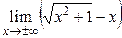 . Критерий оценивания. . Критерий оценивания.
| Понятие функции. Область определения функции. Теоремы о пределе суммы, разности, произведения, частного. Теоремы о бесконечно больших и бесконечно малых функциях. Неопределенности вида 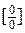 , , 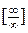 , , 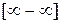 . . | |||||||||||||
| Промежуточный контроль | |||||||||||||||
| Модуль 2. Пределы трансцендентных функций | |||||||||||||||
| Аудиторная работа | |||||||||||||||
| Самостоятельная работа № 1 «Вычисление пределов тригонометрических функций» | Примеры заданий.Уметь вычислять пределы тригонометрических функций. Например, 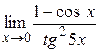 . Критерий оценки: 2 балла – пример решен правильно, 1 балл – пример решен с незначительными ошибками, 0 баллов – пример не решен. . Критерий оценки: 2 балла – пример решен правильно, 1 балл – пример решен с незначительными ошибками, 0 баллов – пример не решен. | Теоремы о пределе суммы, разности, произведения, частного. Теоремы о бесконечно больших и бесконечно малых функциях. Неопределенности вида 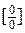 , , 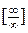 . . | |||||||||||||
| Самостоятельная работа № 2 «Вычисление пределов показательно-степенных функций» | Примеры заданий.Уметь вычислять пределы показательно-степенных функций. Например, 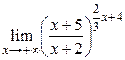 . Критерий оценки: 2 балла – пример решен правильно, 1 балл – пример решен с незначительными ошибками, 0 баллов – пример не решен. . Критерий оценки: 2 балла – пример решен правильно, 1 балл – пример решен с незначительными ошибками, 0 баллов – пример не решен. | Теоремы о пределе суммы, разности, произведения, частного. Теоремы о бесконечно больших и бесконечно малых функциях. Неопределенности вида 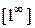 . . | |||||||||||||
| Контрольное мероприятие по модулю | |||||||||||||||
| Теоретическая часть (коллоквиум) | Перечень вопросов. 1. Предел целой рациональной функции при 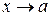 и и 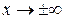 . 2. Предал дробно рациональной функции при . 2. Предал дробно рациональной функции при 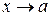 и и 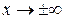 . 3. Теоремы о пределах, связанные с неравенствами: о сохранении функцией знака своего предела; о переходе к пределу в неравенстве; о пределе промежуточной функции. 4. Предел тригонометрических функций. Первый замечательный предел, следствия их него. 5. Предел показательной и логарифмической функции. Понятие показательно-степенной функции. Теорема о пределе показательно-степенной функции. Виды неопределенностей в случае показательно-степенной функции. Второй замечательный предел. Критерий оценивания. . 3. Теоремы о пределах, связанные с неравенствами: о сохранении функцией знака своего предела; о переходе к пределу в неравенстве; о пределе промежуточной функции. 4. Предел тригонометрических функций. Первый замечательный предел, следствия их него. 5. Предел показательной и логарифмической функции. Понятие показательно-степенной функции. Теорема о пределе показательно-степенной функции. Виды неопределенностей в случае показательно-степенной функции. Второй замечательный предел. Критерий оценивания.
| ||||||||||||||
| Практическая часть (контрольная работа) | Вычислить пределы функций, формулируя используемые теоремы о пределах: а) 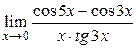 , б) , б) 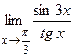 , в) , в) 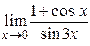 г) г) 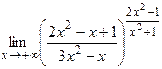 , д) , д) 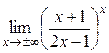 , е) , е) 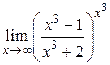 . Критерий оценивания. . Критерий оценивания.
| Теоремы о пределе суммы, разности, произведения, частного. Теоремы о бесконечно больших и бесконечно малых функциях. Неопределенности вида 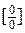 , , 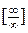 , , 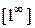 . . | |||||||||||||
| Промежуточный контроль |
Преподаватель Барова Е.А., к.ф.-м.н., доцент кафедры математики и методики обучения
