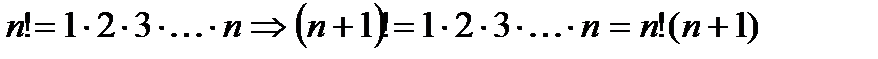Свойства бесконечно малых и бесконечно больших последовательностей.
1) Пусть 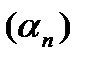 бесконечно малая и при всех
бесконечно малая и при всех 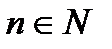
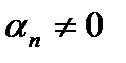 . Тогда
. Тогда 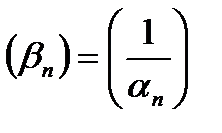 является бесконечно большой.
является бесконечно большой.
2) Пусть 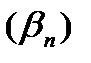 бесконечно большая и
бесконечно большая и 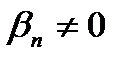 при всех
при всех 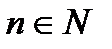 . Тогда
. Тогда 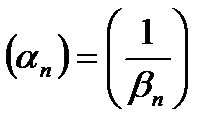 является бесконечно малой.
является бесконечно малой.
3) Если 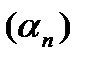 и
и 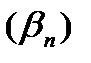 бесконечно малые, то
бесконечно малые, то 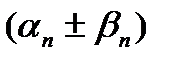 ,
, 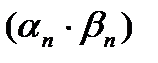 являются бесконечно малыми.
являются бесконечно малыми.
4) Если 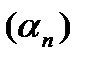 бесконечно малая и
бесконечно малая и 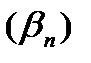 ограниченная последовательность, то
ограниченная последовательность, то 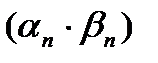 является бесконечно малой.
является бесконечно малой.
Последовательность 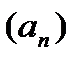 называется ограниченной, если существует число
называется ограниченной, если существует число 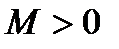 такое, что при всех
такое, что при всех 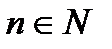 выполняется условие:
выполняется условие: 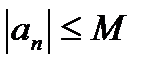 .
.
В частности, постоянная последовательность 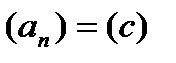 , где
, где  - число, является ограниченной.
- число, является ограниченной.
Можно доказать, что сходящаяся последовательность является ограниченной. Следовательно, к постоянной или сходящейся последовательности 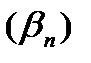 можно применять свойство 4): при умножении
можно применять свойство 4): при умножении 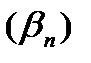 на бесконечно малую
на бесконечно малую 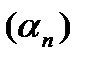 получим бесконечно малую
получим бесконечно малую 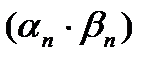 .
.
Свойства можно использовать для вычисления пределов, причем свойства 3) и 4) распространяются на любое конечное число слагаемых и множителей.
Примеры. Найти пределы:
1) 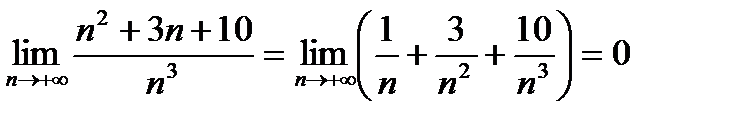 , так как
, так как 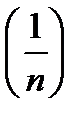 ,
, 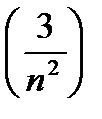 и
и 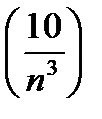 являются бесконечно малыми и их сумма тоже.
являются бесконечно малыми и их сумма тоже.
2) 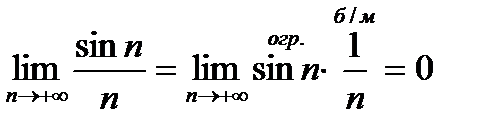 , так как
, так как 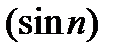 - ограниченная и
- ограниченная и 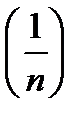 - бесконечно малая. Тогда их произведение является бесконечно малой.
- бесконечно малая. Тогда их произведение является бесконечно малой.
3) 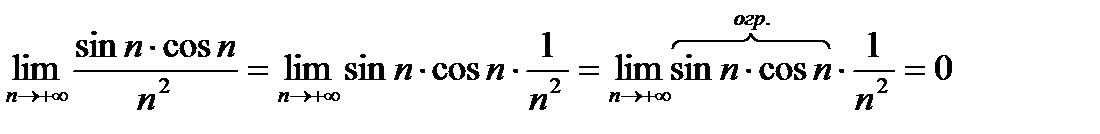 или по-другому
или по-другому 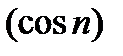 - ограниченная,
- ограниченная, 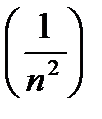 - бесконечно малая
- бесконечно малая 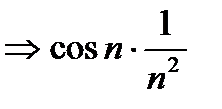 бесконечно малая. Далее
бесконечно малая. Далее 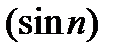 ограниченная и
ограниченная и 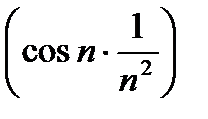 бесконечно малая.
бесконечно малая.
Действия с пределами.
Даны 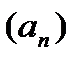 и
и 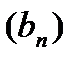 - две последовательности. Их суммой (разностью) называется последовательность
- две последовательности. Их суммой (разностью) называется последовательность 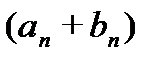
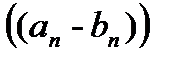 ; их произведением называется последовательность
; их произведением называется последовательность 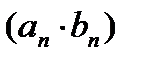 ; их частным называется последовательность
; их частным называется последовательность 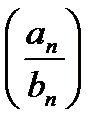 , если
, если 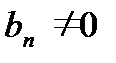 при всех
при всех 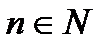 .
.
Теорема. Если 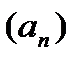 сходится к
сходится к 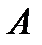 и
и 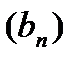 сходится к
сходится к 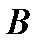 , то
, то 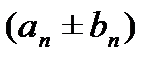 ,
, 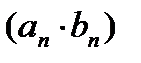 и
и 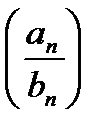 при
при 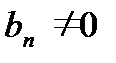 для всех
для всех 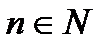 являются сходящимися, причем
являются сходящимися, причем 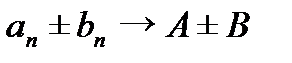 ;
; 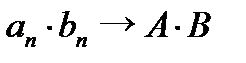 и
и 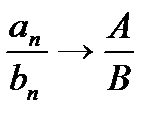 , если
, если 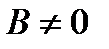 .
.
Эту теорему можно сформулировать по-другому:
Теорема.Если существует 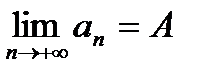 и
и 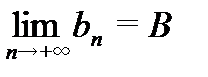 ,
, 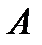 и
и 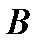 - числа, то существуют конечные пределы суммы, произведения и частного при
- числа, то существуют конечные пределы суммы, произведения и частного при 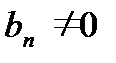 для всех
для всех 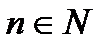 , при этом:
, при этом: 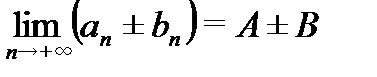 ;
; 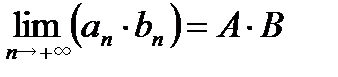 и
и 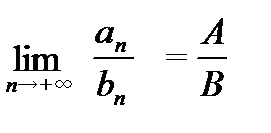 , если
, если 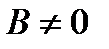 .
.
Теорема применяется при вычислении пределов, при этом дополнительно могут использоваться и свойства бесконечно малых и бесконечно больших.
Примеры. Найти пределы
1) 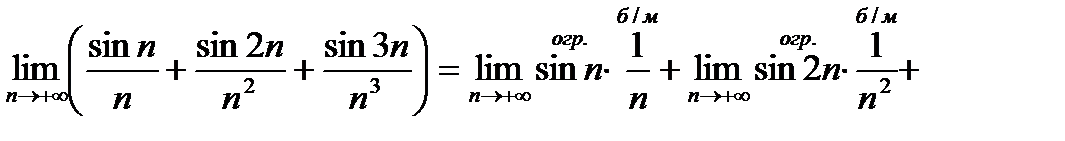
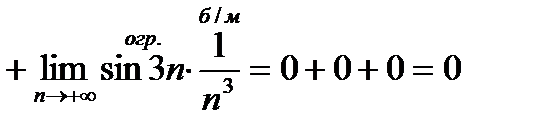
2) 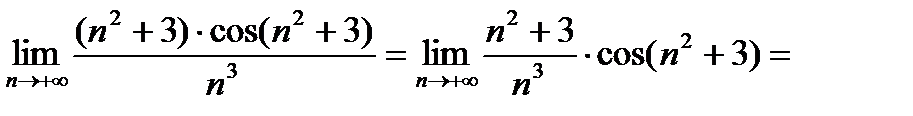
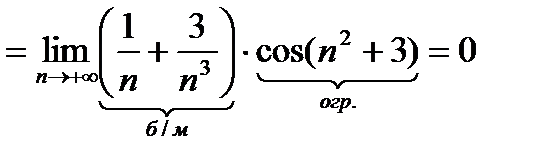
3) 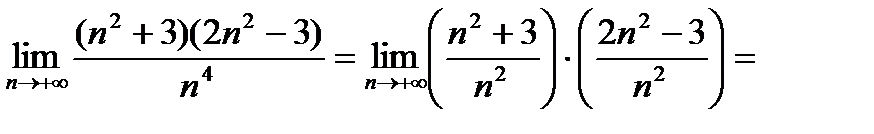
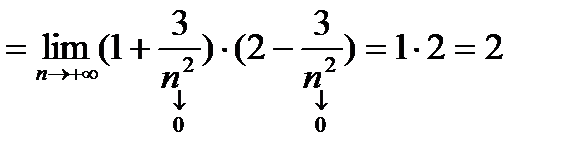
Неопределенности.
Теорема о действиях с пределами справедлива лишь в случае, если 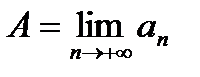 и
и 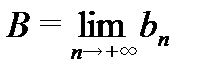 являются числами. Можно доказать обобщенную теорему о действиях с пределами, в которой возможны равенства
являются числами. Можно доказать обобщенную теорему о действиях с пределами, в которой возможны равенства 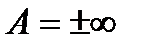 ,
, 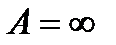 ,
, 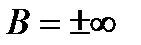 ,
, 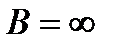 и
и 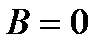 в случае частного
в случае частного 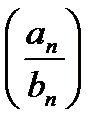 . Запишем выводы обобщенной теоремы символически, например, справедливо: если
. Запишем выводы обобщенной теоремы символически, например, справедливо: если 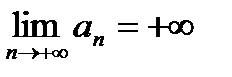 ,
, 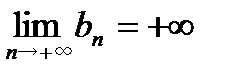 , то
, то 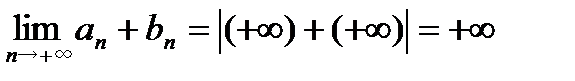 . Из этой строгой записи оставим только символическую запись:
. Из этой строгой записи оставим только символическую запись: 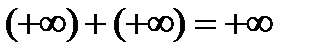 . Далее всю теорему запишем символически.
. Далее всю теорему запишем символически.
Обобщенная теорема.
1) 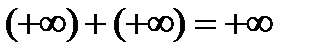
2) 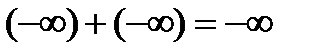
3) 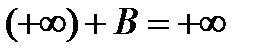 ,
, 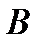 - число
- число
4) 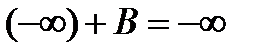 ,
, 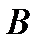 - число
- число
5) 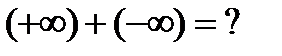 - неопределенность
- неопределенность
6) 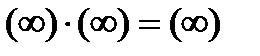
7) 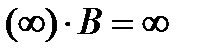 , если
, если 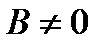
8) 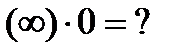 - неопределенность
- неопределенность
9) 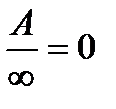 ,
, 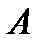 - число
- число
10) 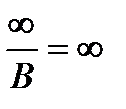 ,
, 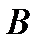 - число
- число
11) 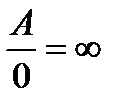 ,
, 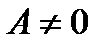
12) 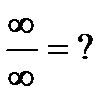 - неопределенность
- неопределенность
13) 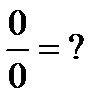 - неопределенность
- неопределенность
Рассмотрим конкретные примеры.
1) 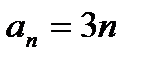 ,
, 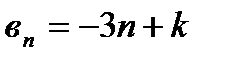 , k – любое число.
, k – любое число.
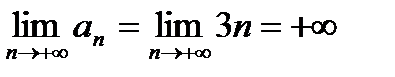 ,
, 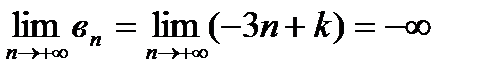
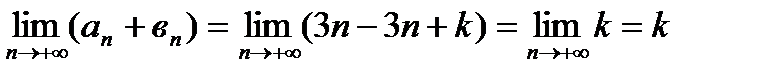 .
.
Можно взять конкретные k: k=3, k=0, k=5.
2) 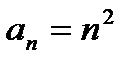 ,
, 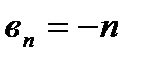
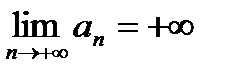 ,
, 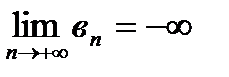
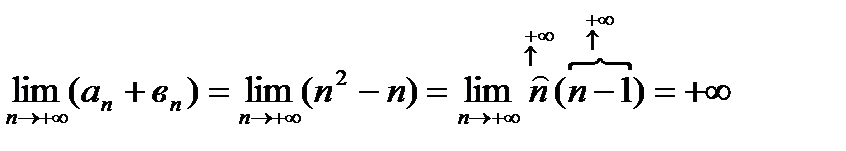
3) 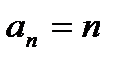 ,
, 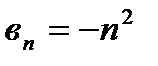
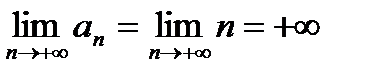 ,
, 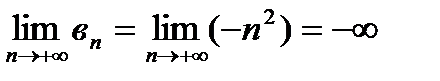
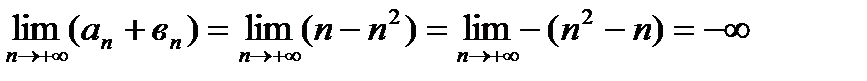
4) 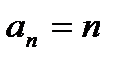 ,
, 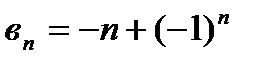
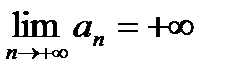 ,
, 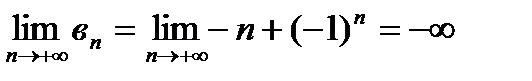
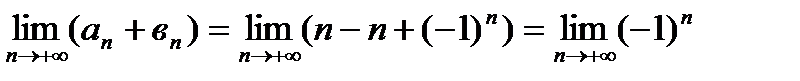 не существует, так как последовательность
не существует, так как последовательность 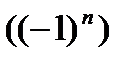 или подробнее -1, +1, -1, +1, -1, +1,... не может стремиться ни к какому числу.
или подробнее -1, +1, -1, +1, -1, +1,... не может стремиться ни к какому числу.
Таким образом, складывая 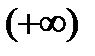 и
и 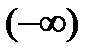 можем получить любое число k, можем получить также
можем получить любое число k, можем получить также 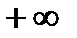 ,
, 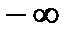 , можем получить отсутствие предела. Это и считается неопределенностью, в отличие, скажем, от пункта 6), где при любых конкретных
, можем получить отсутствие предела. Это и считается неопределенностью, в отличие, скажем, от пункта 6), где при любых конкретных 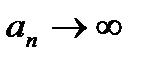 и
и 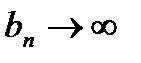 обязательно получится, что
обязательно получится, что 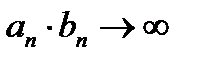 .
.
Обобщенная теорема позволяет расширить границы решаемых примеров, но не дает ответа в случаях неопределенностей 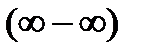 ,
, 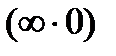 ,
, 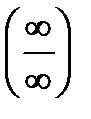 и
и 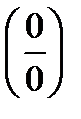 , так как в этих случаях ответа в общем виде нельзя дать – ответ зависит от конкретных последовательностей. Нахождение предела в случае неопределенности называется раскрытием неопределенности. Существует ряд приемов раскрытия неопределенностей, которые рассмотрим на примерах.
, так как в этих случаях ответа в общем виде нельзя дать – ответ зависит от конкретных последовательностей. Нахождение предела в случае неопределенности называется раскрытием неопределенности. Существует ряд приемов раскрытия неопределенностей, которые рассмотрим на примерах.
Примеры. Найти пределы:
1) 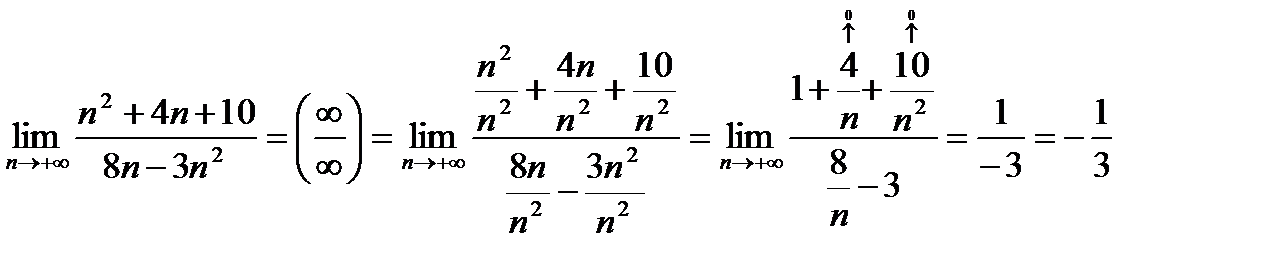
Такой способ решения называется делением числителя и знаменателя на 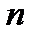 в высшей степени (здесь
в высшей степени (здесь 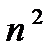 ) для неопределенности
) для неопределенности 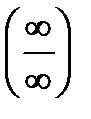 .
.
2) 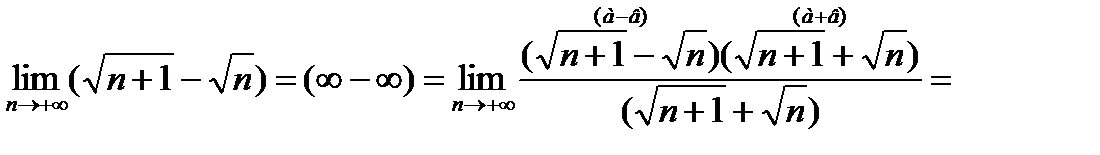
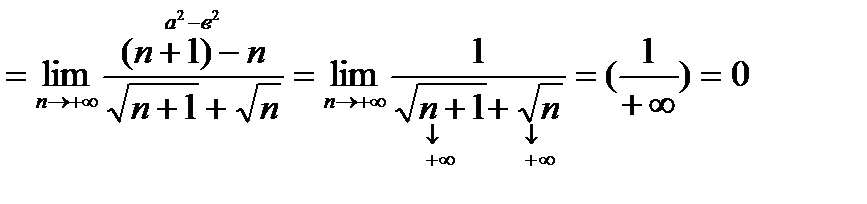
Такой способ называется умножением числителя и знаменателя на выражение, сопряженное числителю или знаменателю.
3) 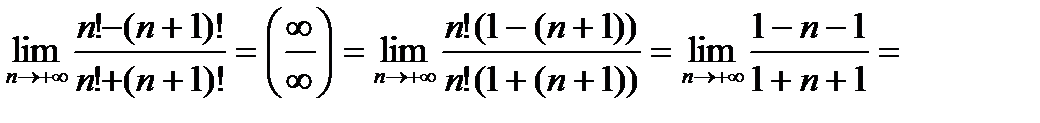
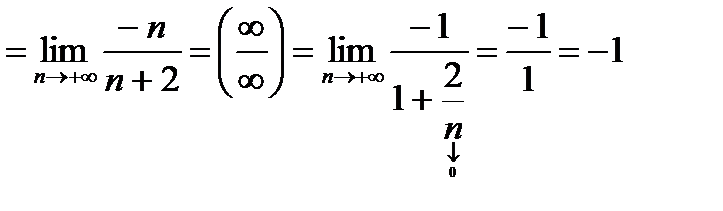
Этот способ называется сокращением на общий множитель (здесь 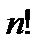 ) числителя и знаменателя. Кроме того, использовали деление на высшую степень.
) числителя и знаменателя. Кроме того, использовали деление на высшую степень.
Напомним, что