Исследование функций на выпуклость и вогнутость. Точки перегиба. Асимптоты.

График функции 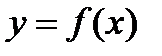называется выпуклым (вогнутым) на интервале 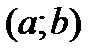, если он расположен ниже (выше) касательной, проведенной в любой точке кривой, соответствующей этому интервалу (рис .1).

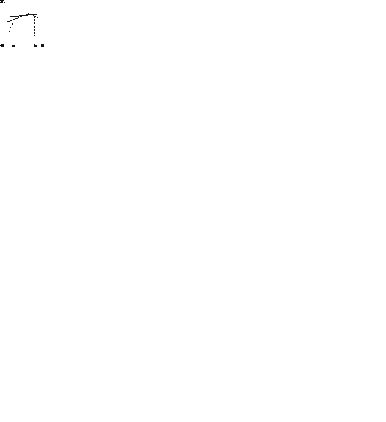
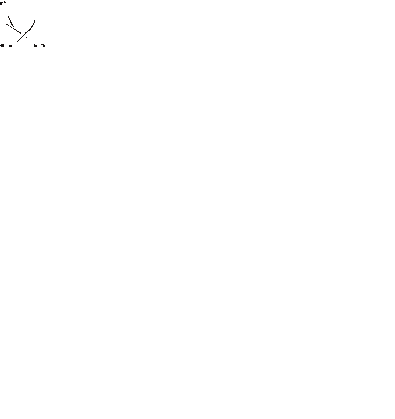
рис. 1 рис. 2

Достаточное условие выпуклости (вогнутости) графика функции.

Пусть 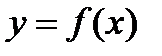дважды дифференцируема на 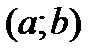. Если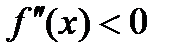 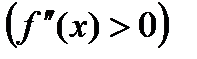на интервале 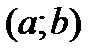, то график функции является выпуклым (вогнутым) на этом интервале.

Точка 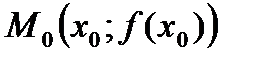графика функции 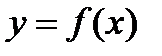, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба (рис. 2).

Необходимое условие точки перегиба.

Если 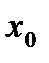- абсцисса точки перегиба графика функции 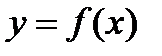, то вторая производная в этой точке равна нулю или не существует.

Точки, в которых вторая производная равна нулю или не существует, называются критическими точками II-го рода.

Достаточное условие точки перегиба.

Пусть функция 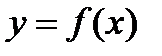имеет вторую производную в некоторой окрестности критической точки 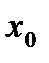. Тогда если в пределах указанной окрестности 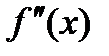имеет разные знаки слева и справа от точки 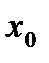, то график функции имеет перегиб в точке .

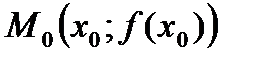Другими словами, если при переходе через критическую точку 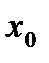вторая производная меняет знак, то точка 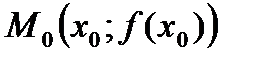есть точка перегиба.

Асимптотой кривой называется прямая, к которой неограниченно приближается точка кривой при неограниченном удалении её от начала координат.

1. Прямая 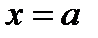является вертикальной асимптотой кривой 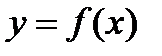, если 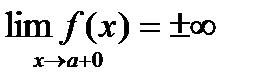или .

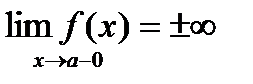2. Прямая 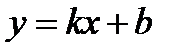является наклонной асимптотой кривой 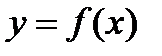тогда и только тогда, когда существуют конечные пределы

,

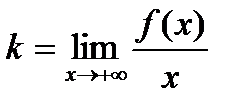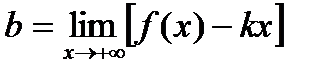
или

, .

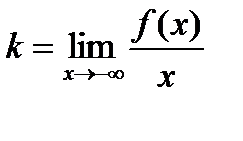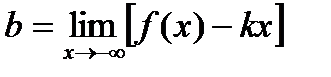Частным случаем наклонной асимптоты пр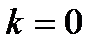и и 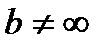является горизонтальная асимптота. Существование горизонтальной асимптоты выявляется проще, чем существование наклонной асимптоты. Дадим специальное правило нахождения асимптоты в этом случае.

3. Прямая 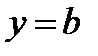является горизонтальной асимптотой кривой 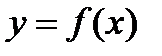, если существует конечный предел 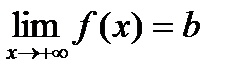или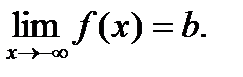

Пример 1. Найти точки перегиба и промежутки выпуклости и вогнутости функции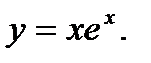

Решение. Область определения функции – вся числовая прямая.

Находим производные:

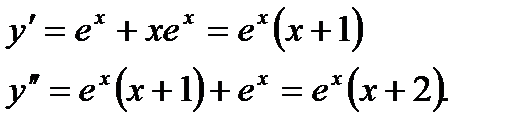
Приравняв к нулю вторую производную, получим критические точки второго рода:

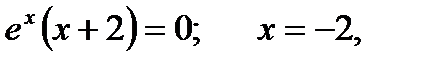так как 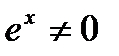для любых .

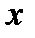Отметив точку 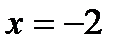на вспомогательном рисунке и исследовав знак второй производной в её окрестности, получаем слева от точки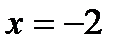 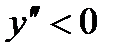(кривая выпуклая), а справа - 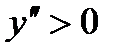(кривая вогнутая). Таким образом, при переходе через точку 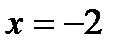вторая производная меняет знак, следовательно точка с абсциссой 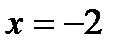является точкой перегиба графика рассматриваемой функции. Ее координаты .

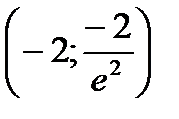Таким образом, на интервале 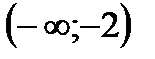кривая выпуклая, а на интервале 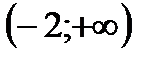- вогнутая, 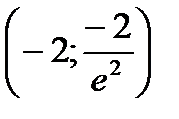- точка перегиба.

Пример2. Найти асимптоты кривой .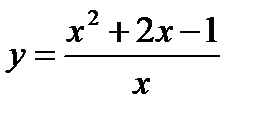

Решение.

Область определения функции .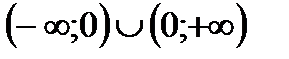

Ищем вертикальные асимптоты:

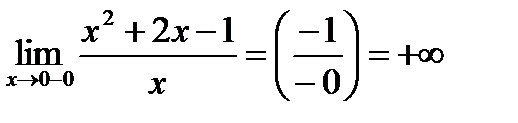
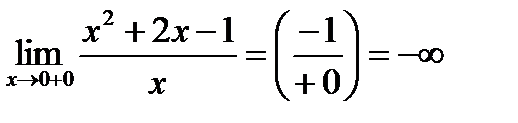
Следовательно, прямая 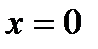, т.е. ось 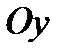есть вертикальная асимптота (и слева, и справа).

Горизонтальных асимптот нет, так как

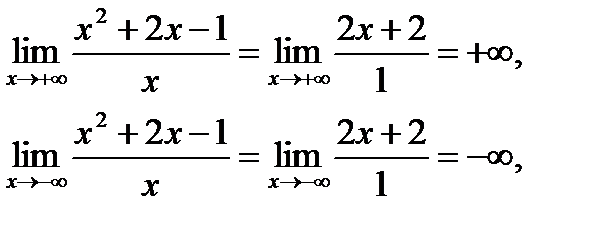
т.е. оба предела не существуют (при вычислении пределов использовалось правило Лопиталя).

Ищем наклонные асимптоты:

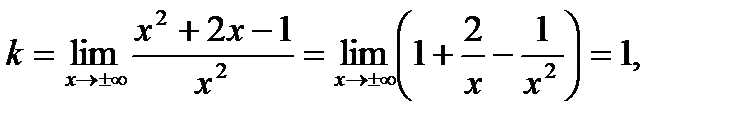т.е.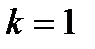

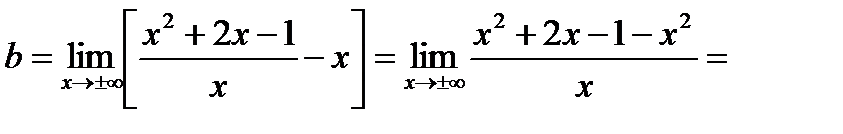
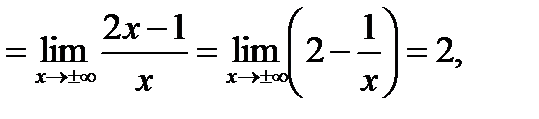
т.е. .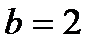

Следовательно, прямая 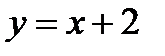есть наклонная асимптота и влево, и вправо данной кривой (рис. 3).

Рис. 3