Основные свойства определителей 3-го порядка

МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ

Определители 2-го порядка

1. Определения. В ряде вопросов математики используются некоторые специальные выражения, называемые определителями (или детерминантами). Простейшие из них – это так называемые «определители 2-го порядка». Покажем, как эти определители возни­кают при решении системы двух линейных уравнений с двумя неиз­вестными.

Рассмотрим систему

а₁x + b₁y = c₁,

а₂x + b₂y = c₂.

Чтобы исключить неизвестное у, умножим второе уравнение на b₁ и вычтем то, что получится, из первого уравнения, умноженного на b₂. В результате окажется

(а₁ b₂ – а₂ b₁) х = c₁ b₂ – c₂ b_1.

Коэффициент при х записывается в виде 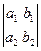и называется определителем 2-го порядка. Таким образом, опреде­литель 2-го порядка есть некоторое число, определяемое как числами а₁, а₂, b₁, b₂, так и их взаимным расположением. Это расположение задается квадратной таблицей .

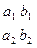Чтобы подчеркнуть, что эта таблица рассматривается как нечто целое, ее окаймляют круглыми скобками или двумя парами вертикальных чёрточек: 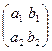или .

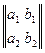Такие таблицы называют матрицами 2-го порядка. Про определитель говорят, что он порождён матрицей. Необходимо чётко понимать разницу между определителем 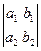и матрицей 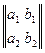. Первый есть число, а вторая – просто таблица, составленная из четырёх чисел.

Итак, определителем матрицы называется число, находимое по формуле:

Det 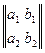= а₁ b₂ – а₂ b₁.

Числа а₁, а₂, b₁, b₂ называют элементами определителя и порождающей его матрицы. Различают также первый столбец 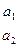и второй столбец 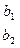, первую строку 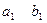и вторую строку 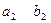. Строки и столбцы определителя называют рядами. Пара чисел а₁, b₂ образуют главную диагональ (+) определителя, пара чисел а₂, b₁ – вторую диагональ (–).

Примеры.

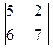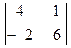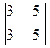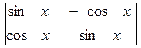= 35 – 12 = 23; = 24 + 2 = 26; = 0; = 1.

Основные свойства определителей 2-го порядка.

I. Определитель не изменится, если его строки превратить в столбцы, а столбцы в строки (равноправность строк и столбцов):

= .

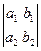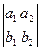II. При перестановке строк (столбцов) определитель меняет знак:

= – .

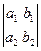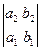III. Если строки (столбцы) определителя одинаковы, то определитель равен нулю: 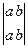=0.

IV. Если все элементы одной из строк определителя умножить на некоторое число, то весь определитель умножится на это число, т.е. общий множитель элементов одной строки можно вынести за знак определителя:

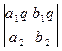=q .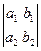

V. Если элементы одной строки пропорциональны элементам другой, то определитель равен нулю:

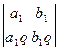=0.

VI. Если к одной из строк прибавить другую, умноженную на любое число, то определитель не изменится:

= .

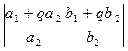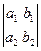Определители 3-го порядка

1. Определение.Определителем третьего порядка называется число:

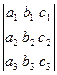= a₁ b₂ c₃ + a₂ b₃ c₁ + a₃ b₁ c₂ – a₃ b₂ c₁ – a₂ b₁ c₃ – a₁ b₃ c₂ .

Примеры.

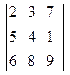= 72 + 280 +18 – 168 – 135 – 16 = 51.

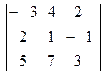= -9 + 28 – 20 – 10 – 24 – 21 = – 56.

Основные свойства определителей 3-го порядка.

Те же свойства, что и у определителей 2-го порядка.