Основные свойства определителей

Высшая математика.

1. Действия с матрицами: умножение на число, сложение, вычитание, умножение матриц. Свойства операций над матрицами.

Матрицей размера 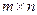называется прямоугольная таблица чисел, содержащая т строк и п столбцов.

Матрица, у которой число строк равно числу столбцов 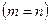, называется квадратной матрицей порядка п. Нулевой называется матрица, все элементы которой равны нулю. Ее обозначают буквой О.

Диагональной называется квадратная матрица, у которой все элементы, стоящие не на главной диагонали, равны нулю. Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной и обозначается буквой Е.

Для матриц одинакового размера вводятся операции сложения и вычитания.

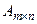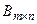Для того чтобы сложить две матрицы и , достаточно сложить их соответствующие элементы. Операция обозначается .

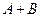Для того чтобы из матрицы 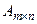вычесть матрицу 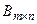, достаточно из каждого элемента матрицы А вычесть соответствующие элементы матрицы В. Операция обозначается .

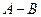Для того чтобы матрицу 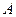умножить на число 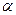, достаточно все элементы матрицы 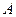умножить на число 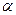. Операция обозначается 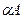или .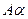

Произведение матрицы 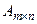на матрицу 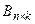вводится только для согласованных матриц, т. е. число столбцов матрицы 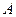должно равняться числу строк матрицы 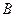(число п). Операция обозначается .

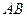Произведениемматриц 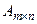и 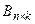называется такая матрица 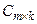, каждый элемент которой 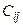равен сумме произведений элементов i-й строки матрицы 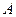на соответствующие элементы j-го столбца матрицы .

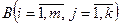Произведение матриц не обладает свойством коммутативности, т. е. не всегда 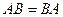, даже если произведения имеют смысл.

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной. Ее обозначают .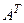

2. Определители 2-го и 3-го порядков. Свойства определителей.

Определителем второго порядка матрицы 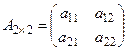называется число, равное произведению элементов главной диагонали минус произведение элементов побочной диагонали, т. е.

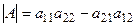. (1.1)

Определителем третьего порядка матрицы

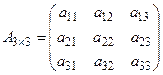называется число, вычисляемое по формуле

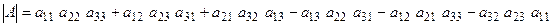. (1.2)

Чтобы составить выражение (1.2), используют символическое правило треугольников (правило Саррюса):

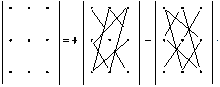
Основные свойства определителей

1. Определитель матрицы не изменяется при ее транспонировании, т. е.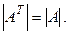

2. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.

3. Общий множитель всех элементов какой-либо строки (столбца) матрицы можно вынести за знак ее определителя.

4. Определитель матрицы с нулевой строкой (столбцом) равен нулю.

5. Определитель матрицы не изменится, если к элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

6. Определитель матрицы с двумя пропорциональными строками (столбцами) равен нулю.

7. Определитель произведения двух квадратных матриц равен произведению их определителей, т. е. .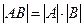

3. Миноры и алгебраические дополнения. Вычисление определителей с помощью формул разложения.

Минором 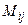элемента 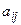квадратной матрицы А п-го порядка называется число, равное определителю (п-1)-го порядка матрицы, полученной из матрицы А вычеркиванием i-й строки и j-го столбца, .

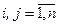Алгебраическим дополнением 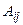элемента 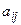матрицы А называется число, равное

.

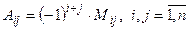Определителем п-го порядка матрицы 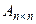называется число, равное сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения:

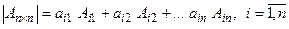, (1.3)

или

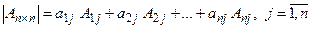. (1.4)

Формулы (1, 3), (1, 4) называются формулами Лапласа разложения определителя по элементам i-й строки, j-го столбца соответственно.

Определитель матрицы не зависит от выбора строки (столбца), по которой идет разложение.

9. Вычислить определитель третьего порядка

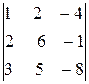
1) по правилу треугольников;

2) по формуле Лапласа.

Р е ш е н и е. 1. По формуле (1.2) непосредственно находим

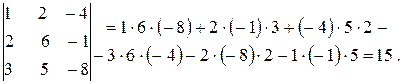
2. Разложим определитель по элементам первой строки. Тогда из формулы (1.3) следует

.

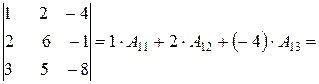
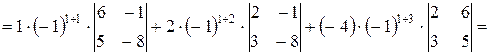
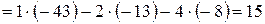10. Показать, что определитель треугольной матрицы равен произведению элементов главной диагонали:

.

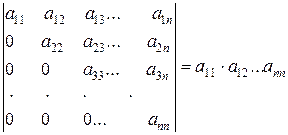Р е ш е н и е. Применим последовательно формулу (1.4) разложения определителя по элементам первого столбца.

Имеем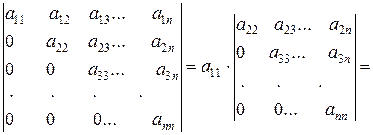

.

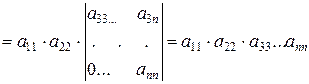В частности, определитель единичной матрицы равен единице, .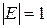

4. Обратная матрица и ее вычисление.

Квадратная матрица А называется невырожденной, если ее определитель не равен нулю (в противном случае называется вырожденной).

Матрица 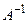называется обратной для матрицы А, если выполняются условия

.

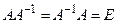Обратная матрица существует только для квадратных невырожденных матриц и находится по формуле

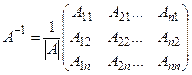, (1.5)

где 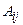– алгебраические дополнения элементов 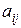матрицы .

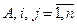5. Ранг матрицы. Вычисление ранга с помощью элементарных преобразований.

Минором к-го порядка матрицы 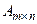называется определитель к-го порядка, составленный из элементов, стоящих на пересечениях выбранных k строк и k столбцов матрицы А.

Рангом матрицы А называется целое число, равное наивысшему порядку не равных нулю миноров этой матрицы, обозначается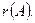

Базисным минором матрицы называется любой не равный нулю минор матрицы, порядок которого равен ее рангу.

По определению ранг нулевой матрицы равен нулю. Ранг матрицы находят либо с помощью метода окаймляющих миноров, либо с помощью элементарных преобразований матрицы.

Элементарными преобразованиями матрицы называются:

1) перемена местами двух строк (двух столбцов);

2) умножение всех элементов какой-либо строки (столбца) на число, не равное нулю;

3) прибавление ко всем элементам некоторой строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число;

4) вычеркивание строки (столбца), состоящей из нулей.

При элементарных преобразованиях матрицы ее ранг не изменяется.

С помощью элементарных преобразований матрицу приводят к такому виду, при котором легко находится базисный минор, порядок которого определяет ранг матрицы.

Видами таких матриц являются треугольная, трапециевидная, ступенчатая матрицы и др.

Примеры

13. Найти ранг матрицы А методом окаймляющих миноров, если

.

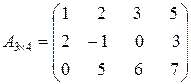Р е ш е н и е. Возьмем минор второго порядка, не равный нулю

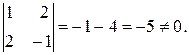
Вычислим окаймляющие его миноры третьего порядка:

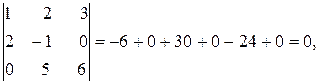
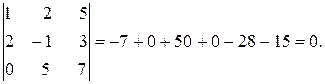
Так как не существует окаймляющих миноров третьего порядка, отличных от нуля, то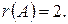

13. Найти ранг матрицы с помощью элементарных преобразований, если

.

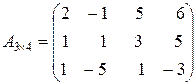Р е ш е н и е. С помощью элементарных преобразований приведем матрицу к трапециевидному виду. Переход от одной матрицы к другой будем обозначать символом ~.

~

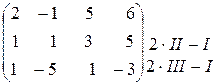из второй строки, умноженной на 2, вычитаем первую строку; из третьей строки, умноженной на 2, вычитаем первую строку

~ ~ .

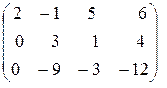
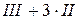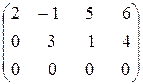Последняя матрица имеет минор второго порядка, не равный нулю:

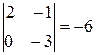, а все миноры третьего порядка равны нулю. Следовательно, .

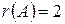14. Найти ранг матрицы при различных значениях параметра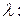

.

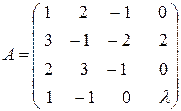Р е ш е н и е.

~ ~

~ ~ .

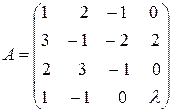
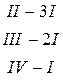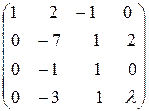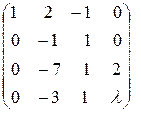
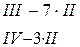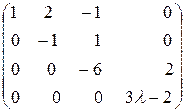При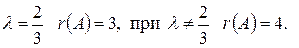

6. Системы линейных алгебраических уравнений. Матричный способ решения систем линейных алгебраических уравнений.

Системой т линейных уравнений с п неизвестными х_1, х₂, …, х_п называется система вида

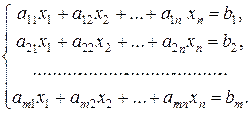(1.6)

Здесь 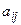– вещественные числа, называемые коэффициентами системы, 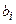– вещественные числа, называемые свободными членами,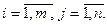

Решением системы (1.6) называется такая упорядоченная совокупность чисел ( 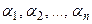), которая будучи подставленной в каждое уравнение системы вместо неизвестных 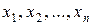превращает их в тождества.

Система (1.6) называется совместной, если она имеет хотя бы одно решение. В противном случае называется несовместной.

Матрица 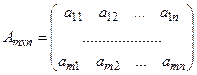– основная матрица системы;

матрица 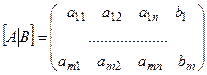– расширенная матрица системы.

– матричная форма системы (1,6).

Здесь 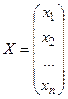– матрица-столбец неизвестных,

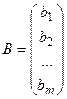– матрица-столбец свободных членов.

Система уравнений (1.6) совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу расширенной матрицы, т. е. 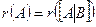(теорема Кронекера – Капелли).

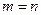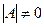Если и , то система (1.6) имеет единственное решение, которое находится

либо матричным способом 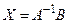, (1.7)

либо по формулам Крамера 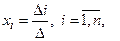(1,8)

где 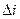– определитель матрицы, полученной из основной матрицы заменой i-го столбца столбцом свободных членов.

В общем случае при решении совместной системы (1.6) выделяют базисный минор и базисные неизвестные (неизвестные, коэффициенты при которых образуют базисный минор основной матрицы). Исходную систему заменяют равносильной, состоящей из тех 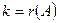уравнений и k базиcных неизвестных, в которые вошли элементы базисного минора. Полученную систему решают либо матричным способом, либо по формулам Крамера, либо методом Гаусса, выражая базисные неизвестные через остальные 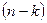свободные неизвестные.

Примеры

16. Три судна доставили в порт 6000 т чугуна, 4000 т железной руды и 3000 т апатитов. Разгрузку можно производить как непосредственно в железнодорожные вагоны для последующей доставки потребителям, так и на портовые склады. В вагоны можно разгрузить 8000 т, а остаток груза придется направить на склады. Необходимо учесть, что поданные в порт вагоны не приспособлены для перевозки апатитов. Стоимость выгрузки 1 т в вагоны составляет соответственно 4,30; 5,25 и 2,20 ден. ед., при отправке на склад – 7,80; 6,40 и 3,25 ден. ед. Записать в математической форме условия полной разгрузки судов, если затраты на нее должны составить 58 850 ден. ед.

Р е ш е н и е. По условию задачи доставленные в порт чугун, железную руду и апатиты можно разгрузить двумя способами: либо в железнодорожные вагоны, либо в портовые склады. Обозначим через 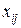количество груза (в тоннах) i-го вида 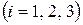, которое предполагается разгрузить 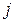-м способом 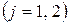. Таким образом, задача содержит шесть неизвестных.

Условие полной разгрузки чугуна можно записать в виде:

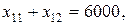
где 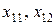– части чугуна, разгружаемого соответственно в вагоны и склады.

Аналогичное условие должно выполняться и для железной руды:

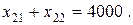
Что же касается апатитов, то их можно разгружать только на склады, а поэтому неизвестная 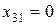и условие полной разгрузки апатитов принимает вид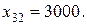

Условие полной загрузки всех поданных в порт вагонов запишется так: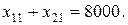

Затраты на разгрузку по условию определены в 58 850 ден. ед., что можно выразить записью:

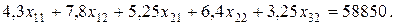
Итак, с учетом сложившейся в порту ситуации условия полной разгрузки прибывших судов выражаются системой линейных уравнений:

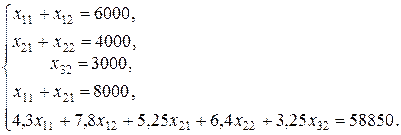
17. Исследовать систему линейных уравнений; если она совместна, то найти ее решение:

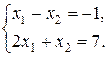
Р е ш е н и е. Запишем расширенную матрицу системы и приведем ее к ступенчатому виду с помощью элементарных преобразований:

~ .

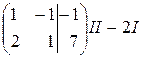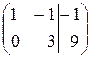Система совместна, т. к. ранг матрицы системы равен рангу расширенной матрицы 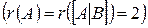. Количество неизвестных также равно 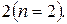Значит, система определена, т. е. имеет единственное решение. Запишем систему уравнений, соответствующую полученной расширенной матрице:

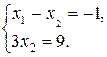
Из второго уравнения 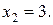Подставляя это значение в первое уравнение, получим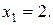

Итак, решение системы .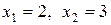

7. Теорема Кронекера-Капелли о совместности системы линейных алгебраических уравнений.

Теорема Кронекера-Капелли.

Для того, чтобы система линейных алгебраических уравнений была совместной (то есть имела решение), необходимо и достаточно, чтобы ранг исходной матрицы системы совпадал с рангом расширенной матрицы, то есть r(A) = r(С).

1) если r(A) = r(С)= n, где n – число неизвестных системы, то данная система имеет единственное решение;

2) если r(A) = r(С) = k < n, то система имеет бесконечное множество решений;

3) если r(A) ≠ r(С), то система несовместна, то есть не имеет решений.

Если число неизвестных больше числа уравнений, то система либо не имеет решений, либо имеет их бесконечное множество (если r(A) = r(С) = =k < n.)

Пример. Исследовать систему уравнений на совместность

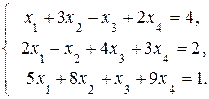
Решение.

Запишем матрицу системы А и определим ее ранг:

.

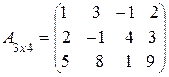Так как матрица А имеет порядок 3´4, то r (A) ≤ 3. Существует

4 различных минора третьего порядка:

, , , .

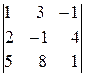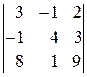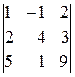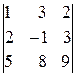Легко проверить, что все эти миноры равны нулю. Например:

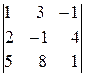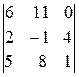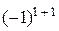
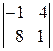= =6ּ +11ּ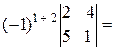

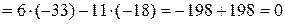
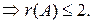
Так как минор второго порядка 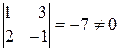,то r (A) = 2.

Рассмотрим расширенную матрицу 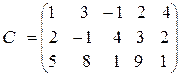. Так как минор третьего порядка

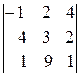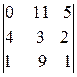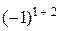
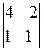= =11ּ +5ּ =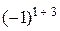

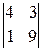= –11ּ2+5ּ33= –22+165=143 ≠ 0, то r(С)=3.

Следовательно, r (A) ≠ r (С), и по теореме Кронекера-Капелли система несовместна, то есть не имеет решений.

Действительно, если первое уравнение системы умножить на 3 и сложить со вторым уравнением, то получим уравнение 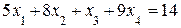. Левая часть этого уравнения совпадает с левой частью третьего уравнения системы, а правые части у них разные. Следовательно, система не имеет решений.

Пример. Исследовать на совместность и решить систему линейных алгебраических уравнений

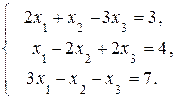(2)

1) с помощью формул Крамера;

2) матричным методом.

Решение.

Запишем матрицу А системы уравнений и определим ее ранг:

.

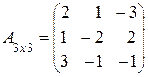Так как 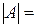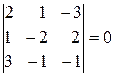(третья строка определителя является суммой первых двух строк), то r(A)< 3. Рассмотрим какой-либо минор

второго порядка: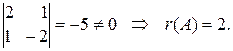

Рассмотрим расширенную матрицу системы: .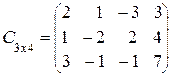

Найдем ее ранг. Существуют 4 различных минора третьего порядка:

, , , .

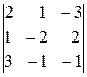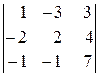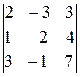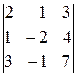Легко проверить, что все эти миноры равны нулю (в каждом из них третья строка есть сумма первых двух строк). Поэтому r (С) < 3. Так как выше рассмотренный минор второго порядка 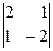принадлежит и матрице С, то

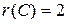, и по теореме Кронекера-Капелли исходная система уравнений совместна (r(A) = r(С)). Но, так как r(A) = r (С) = 2 < 3, где 3 – число неизвестных системы уравнений, то исходная система имеет бесконечное множество решений.

Отличный от нуля минор второго порядка 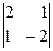состоит из коэффициентов, стоящих при неизвестных 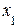и 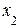первого и второго уравнения. Следовательно, первая и вторая строка матрицы А линейно независимы, а третья выражается через них (является их суммой). Поэтому третье уравнение системы можно отбросить.

Так как элементы данного минора – это коэффициенты пр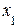и и 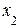, то эти переменные будут базисными, а 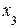«лишней» (свободной), поэтому перенесем ее в правые части уравнений. В итоге получим систему:

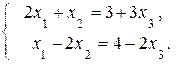(3)

В данном случае определитель матрицы системы 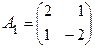не равен нулю. Следовательно, существует обратная матрица 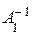, и мы можем решить систему уравнений матричным методом и по формулам Крамера.

8. Формулы Крамера решения систем линейных алгебраических уравнений.

Рассмотрим еще один метод решения системы (1). Пусть, как и ранее, n = m.

Тогда из формулы (3) имеем:

Х= 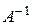В

= =

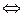
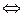
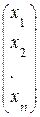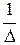
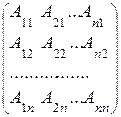
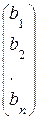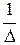
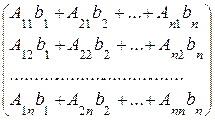
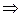
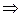
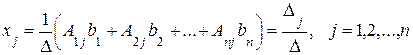. (4)

В формуле (4) 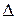= det A – главный определитель системы (1),

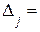
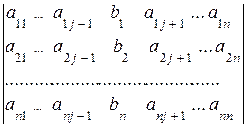= (разлагаем по j-му столбцу)=

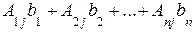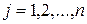= ; , – побочные определители системы (1).

Они получаются из главного определителя заменой соответствующего j-го столбца столбцом свободных членов. Формулы (4) называются формулами Крамера.