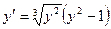V. Неоднородные линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами
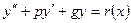
будем решать 2-мя способами.
5.1. Метод вариации произвольной постоянной.
1 шаг. Решаем ОЛДУ:
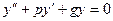
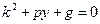
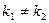
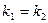
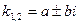
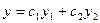
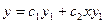
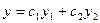
2 шаг. Считаем 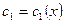 ;
; 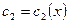 .
.
Подставляем это решение в исходное НЛДУ и получаем систему уравнений для определения 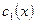 и
и 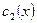 :
:
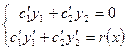
Найдя 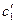 и
и 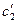 решаем для определения
решаем для определения 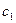 и
и 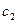 полученные дифференциальные уравнения.
полученные дифференциальные уравнения.
3 шаг. Подставляем найденные 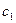 и
и 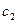 в решение и получаем общее решение НЛДУ.
в решение и получаем общее решение НЛДУ.
Пример 5.1: Решить уравнение 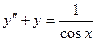 .
.
Решение:
1 шаг. Решаем уравнение 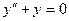 .
.
Его характеристическое уравнение 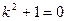 .
.
Отсюда 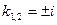
И решение ОЛДУ имеет вид 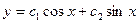 .
.
2 шаг. Считаем 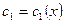 ,
, 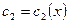 .
.
Имеем систему:
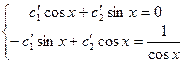 .
.
Решаем эту систему относительно 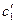 и
и 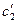 :
:
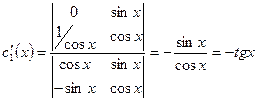
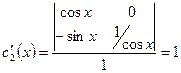 .
.
Т.о. мы получим 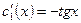
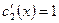 .
.
Решая эти дифференциальные относительно 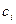 уравнения, получим
уравнения, получим
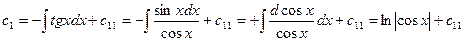 .
.
3 шаг. 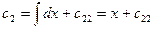 .
.
Отсюда общее решение НЛДУ:
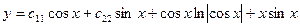 .
.
Пример 5.2: Метод подбора частного решения НЛДУ.
Метод основан на известном утверждении о том, что общее решение НЛДУ есть сумма общего решения ОЛДУ и некоторого частного решения 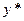 НЛДУ.
НЛДУ.
Общее решение ОЛДУ мы уже умеем исходить.
Частные же решения НЛДУ ищутся по виду 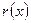 на основе следующих рецептов:
на основе следующих рецептов:
«Правило угадывания частного решения»
Форма f(x): 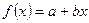 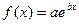 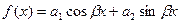 | Форма частного решения: 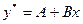 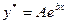 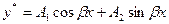 |
1. Угаданное у* надо умножить на х, если
а) 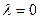 - это один из корней характеристического уравнения и
- это один из корней характеристического уравнения и 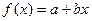 ;
;
в) 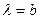 - это один из корней характеристического уравнения и
- это один из корней характеристического уравнения и 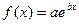 ;
;
с) 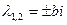 и
и 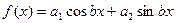 .
.
2. Угаданное у* надо умножить на х2, если
а) 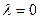 - кратный корень характеристического уравнения и
- кратный корень характеристического уравнения и 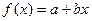 ;
;
в) 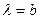 - кратный корень характеристического уравнения и
- кратный корень характеристического уравнения и 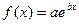 ;
;
Обобщая сказанное, можно для 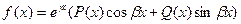 рекомендовать подбор частного решения в виде
рекомендовать подбор частного решения в виде
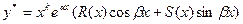 ,
,
где k – кратность корня характеристического уравнения;
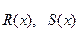 - многочлены, степень которых равна наибольшей из степеней многочленов
- многочлены, степень которых равна наибольшей из степеней многочленов 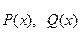 .
.
Пример 5.3.:Решить 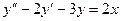
Решение:1 шаг. Решаем однородное уравнение
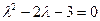
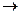
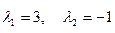
Отсюда 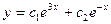
2 шаг. Так как 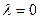 не является корнем характеристического уравнения, то угадываем
не является корнем характеристического уравнения, то угадываем 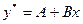 .
.
Подставляя его в исходное уравнение, получим
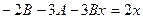 .
.
Приравнивая коэффициенты левой и правой частей, находим
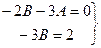
Отсюда 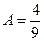 ;
; 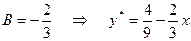 .
.
3 шаг. Искомое решение имеет вид
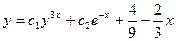 .
.
Пример 5.4.Решить уравнение 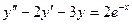 .
.
Решение: 1 шаг. То же, что и в 2.1.5.
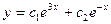
2 шаг. Поскольку в правой части стоит 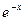 , т.е.
, т.е. 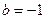 , то мы применяем правило 1.в: -1 также является корнем характеристического уравнения. В связи с этим принимаем
, то мы применяем правило 1.в: -1 также является корнем характеристического уравнения. В связи с этим принимаем
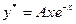 .
.
Подставляем его в исходное уравнение
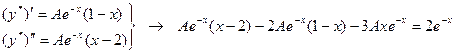 .
.
Упрощая, находим: 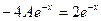 . Отсюда
. Отсюда 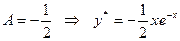
3 шаг. Пишем решение
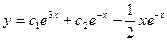
Пример 5.5.Найти решение уравнения 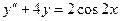 проходящее через точку:
проходящее через точку: 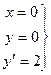
Решение: 1 шаг. Решаем однородные уравнения
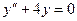
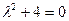
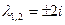
Отсюда 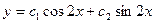 .
.
2 шаг. Поскольку и в корнях 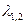 и под знаком cos в правой части уравнения стоит коэффициент 2, то мы имеем случай 1.с. Поэтому
и под знаком cos в правой части уравнения стоит коэффициент 2, то мы имеем случай 1.с. Поэтому
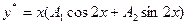 .
.
Найдем производные 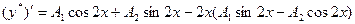
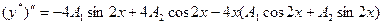 .
.
Подставляем это в исходное уравнение и получаем
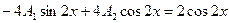 .
.
Отсюда 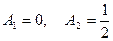 и
и 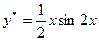 .
.
3 шаг. Общее решение, очевидно, будет
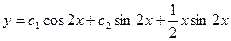 .
.
Найдем с1 и с2 из начальных условий:
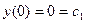
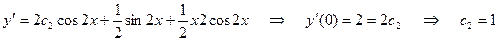
Искомое частное решение имеет вид 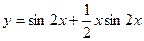 .
.
Пример 5.6. Решить уравнение 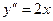
Решение: 1 шаг. Решаем однородное уравнение:
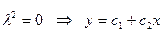
т.к. корень кратный.
2 шаг. Так как 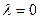 является кратным корнем характеристического уравнения, то ищем
является кратным корнем характеристического уравнения, то ищем 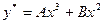
Подставляем это в исходное уравнение
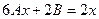
Отсюда 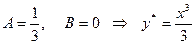 .
.
3 шаг. Общее решение примет вид 
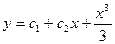 .
.
КОНТРОЛЬНАЯ РАБОТА:
№ 1 Исследовать уравнение на наличие особых решений:
1. 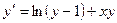
2. 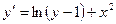
3. 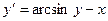
4. 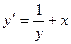
5. 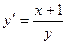
6. 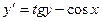
7. 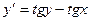
8. 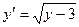
9. 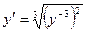
10.