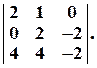Задача № 4. Найти алгебраические дополнения элементов а23 и а31 определителя (см. задачу 3).
Задача № 5. Вычислить определитель, используя подходящее разложение по строке или столбцу
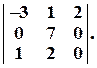
Задача № 6. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элементы какой-либо строки (столбца)
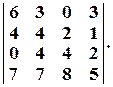
Задача № 7. Вычислить определители приведением их методом Гаусса к треугольному виду
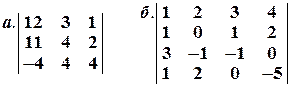
Задача № 8. Решить систему уравнений с помощью правила Крамера:
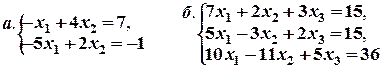
Задача № 9. Вычислить определитель линейной комбинации матриц A, B, BT и AT (AT и BT – матрицы, транспонированные соответственно к матрицам A и B): 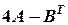 .
.
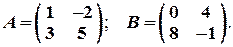
Задача № 10. Умножение матриц
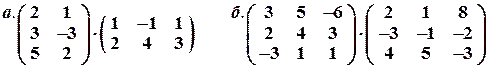
Задача № 11. Вычислить
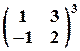
Задача № 12. При каких значениях l матрицы перестановочны?
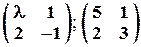
Задача № 13. Найти обратную матрицу
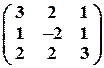
Задача № 14. При каких значениях l матрица не имеет обратную?
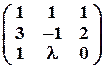
Задача № 15. Решить матричное уравнение:
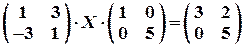
Задача № 16. Решить матричным методом систему уравнений из задачи 8.б.
Задача № 17. При каких значениях l матрица имеет ранг, равный 1?

Задача № 18. Найти ранг матрицы методом Гаусса:
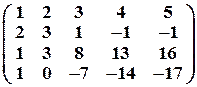
Задача № 19. Решить методом Гаусса системы уравнений:
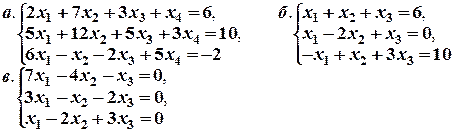
ТИПОВОЙ РАСЧЁТ ПО ЛИНЕЙНОЙ АЛГЕБРЕ
Вариант № 7
Задача № 1. Вычислить определители:
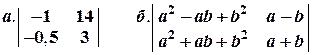
Задача № 2. Решить уравнение
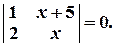
Задача № 3. Вычислить определитель, пользуясь правилом треугольников
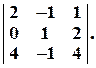
Задача № 4. Найти алгебраические дополнения элементов а23 и а31 определителя (см. задачу 3).
Задача № 5. Вычислить определитель, используя подходящее разложение по строке или столбцу
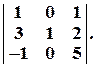
Задача № 6. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элементы какой-либо строки (столбца)
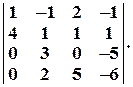
Задача № 7. Вычислить определители приведением их методом Гаусса к треугольному виду
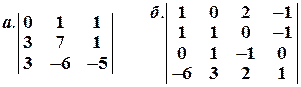
Задача № 8. Решить систему уравнений с помощью правила Крамера:
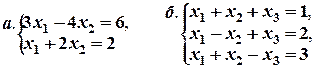
Задача № 9. Вычислить определитель линейной комбинации матриц A, B, BT и AT (AT и BT – матрицы, транспонированные соответственно к матрицам A и B): 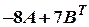 .
.
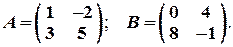
Задача № 10. Умножение матриц
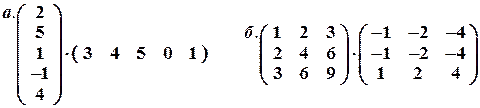
Задача № 11. Вычислить
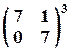
Задача № 12. При каких значениях l матрицы перестановочны?
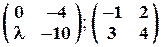
Задача № 13. Найти обратную матрицу
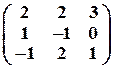
Задача № 14. При каких значениях l матрица не имеет обратную?
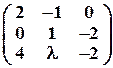
Задача № 15. Решить матричное уравнение:
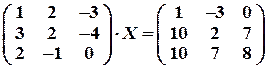
Задача № 16. Решить матричным методом систему уравнений из задачи 8.б.
Задача № 17. При каких значениях l матрица имеет ранг, равный 1?
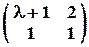
Задача № 18. Найти ранг матрицы методом Гаусса:
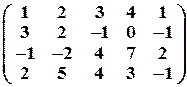
Задача № 19. Решить методом Гаусса системы уравнений:
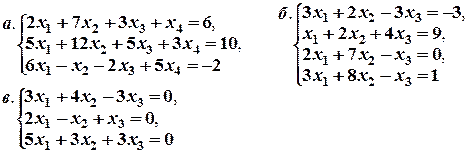
ТИПОВОЙ РАСЧЁТ ПО ЛИНЕЙНОЙ АЛГЕБРЕ
Вариант № 8
Задача № 1. Вычислить определители:
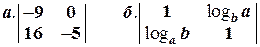
Задача № 2. Решить уравнение
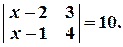
Задача № 3. Вычислить определитель, пользуясь правилом треугольников