Вычисление ранга матрицы «методом окаймляющих миноров».
Правило вычисления ранга матрицы «методом окаймляющих миноров»: при вычислении ранга матрицы следует переходить от миноров меньших порядков к минорам юольших порядков. Если уже найден минор k-ого порядка D, отличный от нуля, то далее вычисляют только миноры (k+1)-ого порядка, окаймляющего минор D: если все они равны нулю, то ранг матрицы равен k.
☺ Пример 79. Найти ранг матрицы: 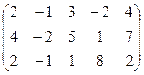 методом окаймляющих миноров.
методом окаймляющих миноров.
Решение: Нетрудно заметить, что минор 2-го порядка: 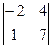 не равен нулю. Это значит, что ранг матрицы не меньше 2. Обозначим окаймляющие миноры 3-го порядка для этого минора:
не равен нулю. Это значит, что ранг матрицы не меньше 2. Обозначим окаймляющие миноры 3-го порядка для этого минора:
| -1 | -2 | ||||
| -2 | |||||
| -1 | |||||
а) выделенный минор 2-го порядка окаймляется столбцами 1, 2, 3 и строкой 3; б) минор 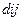 относим к варианту окаймления i–строкой и j–столбцом.
относим к варианту окаймления i–строкой и j–столбцом.
Вычислим выделенные окаймляющие миноры.
| -2 | 1 шаг | -2 | 2 шаг | -2 | ||||||||
| d33 | → | → | -1 | = 0, т.к. строки 2 и3 пропорциональны | ||||||||
| -2 |
1-й шаг: 3C-1С; 2-й шаг: 3R-1R; 2R-1Rх2; 3-й шаг: видим, что определитель равен 0.
| -1 | -2 | 1 шаг | -1 | -2 | 2 шаг | -1 | -2 | |||||
| d32 | -2 | → | -2 | → | -5 | -1 | = 0, т.к. строки 2 и3 пропорциональны | |||||
| -1 | -1 | -10 | -2 |
1-й шаг: 3C+1Сх2; 2-й шаг: 3R-1R; 2R-1Rх2; 3-й шаг: видим, что определитель равен 0.
| -2 | 1 шаг | -2 | 2 шаг | -2 | ||||||||
| d31 | → | → | -1 | = 0, т.к. строки 2 и3 пропорциональны | ||||||||
| -2 |
1-й шаг: 3C-1С; 2-й шаг: 3R-1R; 2R-1Rх2; 3-й шаг: видим, что определитель равен 0.
Т.к. все окаймляющие миноры 3-го порядка равны нулю, то ранг матрицы равен 2.
Ответ: Ранг матрицы равен 2.
Пример 80. Найти ранг матрицы: 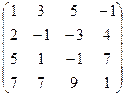 методом окаймляющих миноров.
методом окаймляющих миноров.
Решение: Нетрудно заметить, что минор 2-го порядка: 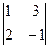 не равен нулю. Это значит, что ранг матрицы не меньше 2.
не равен нулю. Это значит, что ранг матрицы не меньше 2.
Обозначим окаймляющие миноры 3-го порядка для этого минора:
| -1 | ||||
| -1 | -3 | |||
| -1 | ||||
а) выделенный минор 2-го порядка окаймляется столбцами 3, 4 и строками 3, 4; б) минор 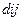 относим к варианту окаймления i–строкой и j–столбцом.
относим к варианту окаймления i–строкой и j–столбцом.
Вычислим выделенные окаймляющие миноры 3-го порядка.
| 1 шаг | 2 шаг | |||||||||||
| d33 | -1 | -3 | → | -1 | -3 | → | -1 | -3 | = 0, т.к. строка 3 нулевая | |||
| -1 |
1-й шаг: 3R-2R х2; 2-й шаг: 3R-1R; 3-й шаг: видим, что определитель равен 0.
| -1 | 1 шаг | -1 | 2 шаг | -1 | ||||||||
| d34 | -1 | → | -1 | → | -1 | = 0, т.к. строка 3 нулевая | ||||||
| -1 |
1-й шаг: 3R-2R х2; 2-й шаг: 3R-1R; 3-й шаг: видим, что определитель равен 0.
| 1 шаг | 2 шаг | |||||||||||
| d43 | -1 | -3 | → | -1 | -2 | → | -1 | -2 | = 0, т.к. строки 1 и3 пропорциональны | |||
1-й шаг: 3С-2С; 3R-1R; 2-й шаг: 3R+2R; 1R +2R; 3-й шаг: видим, что определитель равен 0.
| -1 | 1 шаг | 2 шаг | ||||||||||
| d44 | -1 | → | -1 | → | ≠ 0 | |||||||
| -1 | -3 | -1 | -3 |
1-й шаг: 1R+3R; 3R-1R; 2-й шаг: 2R-3Rх4; 3-й шаг: видим, что определитель ≠ 0. Это значит, что ранг матрицы не меньше 3-х.
Вычислим единственный минор 4-го порядка (определитель матрицы).
| -1 | 1 шаг | -1 | 2 шаг | -1 | |||||||||||||
| -1 | -3 | -1 | -2 | 3 шаг | |||||||||||||
| -1 | = | -2 | = 2∙2 | =4∙1(-1)1+3 | |||||||||||||
1-й шаг: 1С+4С; 3С-2С; 2-й шаг: вынесем за скобку множители 2 столбцов 1 и 3; 3-й шаг: 2R+1R; 3R +1R; 4R -1R; разложим определитель по 3-му столбцу. Видим, что определи-тель равен нулю, т.к. 1-я и 2-я его строки пропорциональны.
Значит, ранг матрицы равен 3.
Ответ: Ранг матрицы равен 3.
☻Решите примеры:
Пример 81. Найти ранг матрицы: 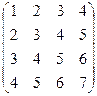 методом окаймляющих миноров.
методом окаймляющих миноров.
Ответ: Ранг матрицы равен 2.
Пример 82. Найти ранг матрицы: 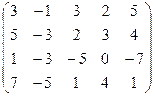 методом окаймляющих миноров.
методом окаймляющих миноров.
Ответ: Ранг матрицы равен 3.
Вопросы для самопроверки:
1. В прямоугольной матрице 5 строк и 9 столбцов. Какому из чисел: 0,1,2,3,4,5,6,7,8,9 может быть равен ранг матрицы?
2. Число независимых столбцов матрицы равно числу независимых строк. Почему?
3. В прямоугольной матрице 5 строк и 9 столбцов. Какое максимальное число окаймляющих миноров придется вычислить при нахождении ранга матрицы?
