А) біріккен үлестірім заңы 3 страница
Б) дайындық сатысы
В) қорытындылау сатысы
Г) негізгі саты
Д) болжау сатысы
119. Стационарлы Пальм ағындарын модельдеу алгаритмінің 2-сатысы
А) негізгі саты
Б) болжау сатысы
В) есептеу сатысы
Г) алдын-ала модельдеу сатысы
Д) қорытындылау сатысы
120. Сыңар емес оқиғалар ағынын модельдеуге алдын-ала даярлану сатысы неше қадамнан тұрады?
А) 3
Б) 5
В) 6
Г) 2
Д) 4
121. Сыңар емес оқиғалар ағынын модельдеу неше сатыдан тұрады
А) 2
Б) 1
В) 6
Г) 4
Д) 3
122. 
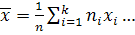формуласымен есептелген арифметикалық орташа .... деп аталады
А) зілдеме орта мән
Б) математикалық үміт
В) дисперсия
Г) тығыздық функциясы
Д) корреляция коэффиценті
123. Тығыздық функциясын ұқсастыру процесі неше сатыдан тұрады?
А) 6
Б) 7
В) 9
Г) 3
Д) 8
124. 
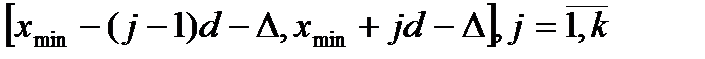Мұндағы jдегеніміз не?
А) интервал номері
Б) тұрақты сан
В) айнымалы
Г) дискретті кездейсоқ шама
Д) қатар номері
125. 
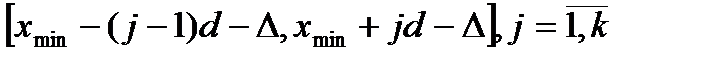мұндағы 
неге тең?
А) 0,001d
Б) 0,01r
В) 2555
Г) ∞
Д) 0.0005d
126. Алдын-ала болжамдалған заңдылықтарды ұқсастыру үшін .............
А) күтілген үлестірім заңдылығы бар кездейсоқ шаманың теориялық ауданын қарастыру керек
Б) берілген таңдаманың мәндер ауданын қарастыру керек.
В) дискретті кездейсоқ шамасының үлестірім заңы ретінде ықтималдықтың кесте арқылы берілген түрін қолдану керек
Г) Колмогоров- Смирнов критерийін қолдану керек
Д) тығыздық функциясын анықтап алу керек
127. Ұқсастырудың үшінші сатысының нәтижесі
А) гистограмма салынады
Б) мониторинг жүргізіледі
В) тығыздық функциясы анықталады
Г) барлығы дұрыс
Д) арифметикалық орта мәні анықталады
128. Пирсонс критерийін қолдануға ыңғайлы жағдай
А) n>100
Б) R<1
В) n<150
Г) -1<n<20
Д) [120,150]
129. Колмогоров-Смирнов критерийі қолданылатын жағдай
А) 10 < n < 100
Б) N<100
В) -1<n<20
Г) R<1
Д) [-∞;∞]
130. Пирсонның х2 критериінің көмегімен үйлестірім заңын ұқсастыру нәтижелерін бағалаудың принципі негізделген теорема
А) η кездейсоқ шамасы мен топтаудың таңдалған к саны қандай болмасын әрбір r > о үшін мына шектіктің дұрыстығына күмән тумайды
Б) R=x2<xa2 шарты орындалған дағдайда, ή кездейсоқ шамасының үлестірім заңын ұқсастыру нәтижесі қабылданады
В) егер а, ықтималдылығы а тең болатын оқиғалар мүмкін емес деп есептелетін мәнділіктің
деңгейі болады
Г) ұқсастыру нәтижесін қабылдау әлде қабылдамау а-ның мәніне тәуелді екені
көрініп тұр. а-ның мәні ретінде көбінесе мына сандар алынады: 0, 25, 14...
Д) бұл заң іс жүзінде ή кездейсоқ шамасының үлестірім заңынан тәуелсіз, ал сынақтың
п санының әсері көп емес.
131. ξ базалық кездейсоқ шамасын түрлендірудің неше бағыты бар?
А) 4
Б) 3
В) 8
Г) 5
Д) 7
132. ξ базалық кездейсоқ шамасын түрлендірудің бағыттары қандай?
А) аналитикалық, таңдамалы, ықтималдылық және құрмаланған.
Б) математиаклық,логикалық және статикалық
В) физикалық,гистограммалық,динамикалық
Г) деференциалдық,логикалық,сұлбалық,деңгейлік
Д) күрделі,логикалық,статикалық
133. Кездейсоқ ξ шамасының zi нақтыламасын аналитикалық түрлендіргенде .....
А) берілгеи үлестірім заңы бар η шамасының нақтыламасы деп қарастыруға болатын х санын анықтайтын операция орындалады.
Б) базалық кездейсоқ тізбектің кейбір сандарын, берілген үлестірім заңына бағынатын жаңа тізбек құратындай етіп таңдап алуға болады.
В) бағыттың қолдану аймағы шектік теоремалар санымен шектеледі.
Г) берілген үлестірім заңына қолданбалы пайдалануға жеткілікті дәлдікпен жақындауды қамтамасыз ететін, ықтималдықтар теориясының шектік теоремалар шарттарын модельдеумен байланысты.
Д) кездейсоқ заңдылықтары үлестірім функциясымен, әлде графикпен, немесе кесте түрінде берілген, кез-келген іс жүзінде мәні бар үздіксіз кездейсоқ шамаларды модельдеуді қамтамасыз етеді.
134. Аналитикалық бағытта көп қолданылатын әдіс -
А) кері функция әдісі
Б) кері графиктік әдіс
В) диаграммалық әдіс
Г) шектеулер жүйесі әдісі
Д) математикалық әдіс
135. Таңдамалы бағыттың негізі мынада-
А) базалық кездейсоқ тізбектің кейбір сандарын, берілген үлестірім заңына бағынатын жаңа тізбек құратындай етіп таңдап алуға болады.
Б) берілген үлестірім заңына қолданбалы пайдалануға жеткілікті дәлдікпен жақындауды қамтамасыз ететін, ықтималдықтар теориясының шектік теоремалар шарттарын модельдеумен байланысты.
В) берілгеи үлестірім заңы бар η шамасының нақтыламасы деп қарастыруға болатын х санын анықтайтын операция орындалады.
Г) кездейсоқ заңдылықтары үлестірім функциясымен, әлде графикпен, немесе кесте түрінде берілген, кез-келген іс жүзінде мәні бар үздіксіз кездейсоқ шамаларды модельдеуді қамтамасыз етеді.
Д) бағыттың қолдану аймағы шектік теоремалар санымен шектеледі
136. Джон фон Нейман әдісі-
А) «шығарып тастау»
Б) кері функция
В) графиктік
Г) динамикалық
Д) математикалық
137. Джон фон Нейман әдісінің қолданылу аясы
А) нақтыламалары жабық [а,ь] кесіндісінде жататын кездейсоқ шамаларды модельдеуде
Б) берілгеи үлестірім заңы бар η шамасының нақтыламасы деп қарастыруға болатын х санын анықтайтын операцияда
В) бағыттың қолдану аймағы шектік теоремалар санымен шектелгенде
Г) графиктік есептерде
Д) динамикалық үлгілеуде
138. Кері функция әдісінің алгоритмі неше қадамнан тұрады?
А) 6
Б) 9
В) 4
Г) 7
Д) 8
139. Кері функция әдісінің алгоритмінің 1-қадамы
А) j = 1 болсын
Б) j > п шартын тексеру
В) η = х егер y<f(x)
Г) кездейсоқ ξ шамасының z нақтыламасын модельдеу.
Д) Р{ξ< z} = z екенін көрсетеді.
140. Кездейсоқ шамаларды модельдеудің қандай әдісі ықтималдықтар теориясының белгілі шектік теоремаларының кейбір шарттарын жуықтап елестетуге негізделген
А) шектік теоремалар әдісі
Б) шығарып тастау әдісі
В) графиктік әдіс
Г) ықтималдықтар теориясы
Д) қалыптастыру әдісі
141. Шектік теоремалар әдісін алғаш рет тұжырымдаған
А) Лаплас
Б) Джон фон Нейман
В) Ньютон
Г) Демокрит
Д) Аристотель
142. Қалыпты үлестірім заңын модельдеу үшін қолданылатын формула
А)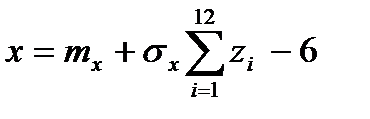 
Б)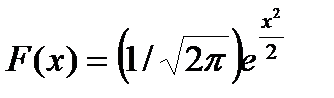 
В)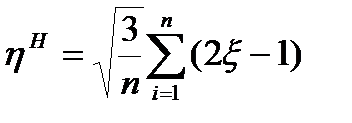 
Г)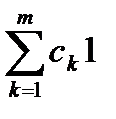 
Д) P{V=k}=(1-p)k-1p=pk
143. Шектік теоремалар әдісі алгаритмі неше қадамнан тұрады?
А) 9
Б) 15
В) 4
Г) 12
Д) 10
144. Т. Бокс пен М. Мюллер ұсынған әдіс
А) орайлық координаттар әдісі
Б) шектеулер әдісі
В) шығарып тастау әдісі
Г) кері функция әдісі
Д) графиктер әдісі
145. Марсалья алгоритмі неше қадамнан тұрады?
А) 8
Б) 9
В) 10
Г) 4
Д) 11
146. Бірқалыпты үлестірім заңының математикалық үміті қандай формуламен есептеледі?
А) M(η)=(a+b)/2
Б) D(η)=(a+b)2/12
В)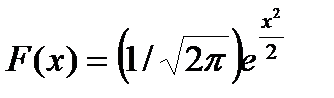
Г) v = [lnξ/ln(1-р)]
Д) n=λ/p
147. Бірқалыпты үлестірім заңының дисперсиясын есептеу формуласы
А) D(η)=(a+b)2/12
Б) n=λ/p
В) M(η)=(a+b)/2
Г) v = [lnξ/ln(1-р)]
Д)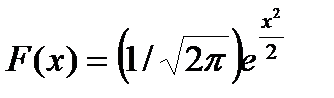
148. Экспотенциалды үлестірім –
А) пайда болу уақытымен сипатталатын біраз нақтылы процестерді бейнелейді
Б) қарапайым ағын оқиғаларының саны дискретті кездейсоқ шама болып табылатын ағын
В) қарқындылықтарының мәні жақын бірнеше басқа ағындарды біріне –бірін қосса қарапайым ағынға жақын ағын алынады
Г) жалпы кешенді алғанда оның технологиялық режимінің стационарлығы
Д) электр қорын өндіру және пайдалану мөлшерлерінің әртүрлі жағдайларға байланысты кездейсоқ өзгерістерін имитациялау
149. Экспотенциалдық үлестірімге жатады-
А) электрон аппараттарының істен шықпай жұмыс істеу ұзақтығы
Б) ғарышқа ұшқан ракета
В) аспанға лақтырылған доп
Г) теңізде жүзген кеме
Д) анықтама алмаған тұрғындар
150. Экспотенциалдық үлестірімнің математикалық үміті
А) M (η)=m , = 1/λ
Б) D(η)=σx2 =1/λ2
В) D(η)=(a+b)2/12
Г) n=λ/p
Д) v = [lnξ/ln(1-р)]
151. Экспотенциалдық үлестірімнің дисперсиясы
А) D(η)=σx2 =1/λ2
Б) M (η)=m , = 1/λ
В) n=λ/p
Г) v = [lnξ/ln(1-р)]
Д) M(η)=(a+b)/2
152. Сызықты үлестірім заңының математикалық үміті
А) М(η= т, =2/3λ
Б) D(η)=σx2 =1/λ2
В) v = [lnξ/ln(1-р)]
Г) D(η) = σx2= 2/9λ2.
Д) D(η)=(a+b)2/12
153. Сызықты үлестірім заңының дисперсиясы
А) D(η) = σx2= 2/9λ2.
Б) М(η= т, =2/3λ
В) M(η)=(a+b)/2
Г) M (η)=m , = 1/λ
Д) v = [lnξ/ln(1-р)]
154. Дискретті кездейсоқ шаманың белгіленуі
А) V
Б) D
В) L
Г) W
Д) X
155. Геометриялық үлестірімнің математикалық үміті
А) М[v] = тх = (1- р)/р
Б) D[v]=(1-p)/p2 -ге тең
В) v = [lnξ/ln(1-р)]
Г) D(η) = σx2= 2/9λ2
Д) D(η)=σx2 =1/λ2
156. Геометриялық үлестірімнің дисперсиясы
А) D[v]=(1-p)/p2 -ге тең
Б) М[v] = тх = (1- р)/р
В) v = [lnξ/ln(1-р)]
Г) M(η)=(a+b)/2
Д) M (η)=m , = 1/λ
157. 
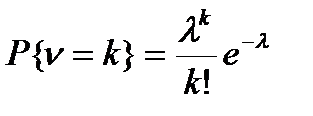Мұндағы λ- дегеніміз не?
А) уақыт бірлігінде алатын окиғалардың орта саны
Б) айнымалы
В) тұрақты сан
Г) математикалық үміт
Д) дисперсия
158. Пуассон үлестірімінің математикалық үміті
А) М[у] = тх=λ
Б) !D[v]=(1-p)/p2 -ге тең
В) D(η) = σx2= 2/9λ2
Г) n=λ/p
Д) v = [lnξ/ln(1-р)]
159. Пуассон үлестірімінің дисперсиясы
А) D[v]=σ2х=λ
Б) М[у] = тх=λ
В) n=λ/p
Г) v = [lnξ/ln(1-р)]
Д) M(η)=(a+b)/2
160. Тығыздық функциясын есептейтін формуланы тап
А)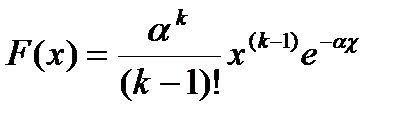 
Б) x=-(1/α)ln(z1)
В)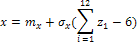 
Г) v = [lnξ/ln(1-р)]
Д) M(η)=(a+b)/2
161. Ғылымда, техникада және экономикада қолданылатын модельдер неше топқа бөлінеді:
А) екі
Б) бір
В) төрт
Г) бес
Д) бөлінбейді
162. Имитациялық модельдеудің түрлері:
А) физикалық және математикалық
Б) статикалық және динамикалық
В) математикалық және логикалық
Г) стратегиялық және ықтималдық
Д) физикалық және динамикалық
163. Физикалық модельдер зерттеліп отырған процестерді оның қандай мәнін сақтай отырып бейнелейді?
А) физикалық
Б) математикалық
В) логикалық
Г) экономикалық
Д) динамикалық
164. Физикалық модель немен ерекшеленеді?
А) өзінің түпнұсқасынан көбінесе өлшемімен ғана
Б) өзінің түп нұсқасынан көбінесе сапасымен ғана
В) өзінің сақтау қабілетімен ғана
Г) өзінің атымен ғана
Д) уақыттың есептелуімен ғана
165. Физикалық модельдер қандай нәтиже береді?
А) нақтылы және арнайы, айқын және сенімді
Б) болжамды және белгісіз, тиімді және қолайлы
В) сенімді және тиімді, нақтылы және қолайлы
Г) белгілі, аумақты, қолайлы және нақтылы
Д) белгілі және сапалы, қолданбалы және нақтылы
166. Имитациялық модель қай салада қолданылады?
А) кәсіпорынның жұмыс барысының бағдарламасын жасау
Б) қару жарақ қолдану
В) қоғамға қызмет көрсету
Г) дағдарыстың себебін анықтау
Д) оқу барысын қадағалау
167. Имитациялық модельдеу деп ...
А) эксперимент жүргізуге бейімделген сандық әдіс
Б) математикалық өрнектермен бейнеленетін құбылыстарды қарастыру әдісі
В) физикалық мәнін сақтай отырып бейнеленетін әдіс
Г) жоспар жасауға бейімделген әдіс
Д) есеп шығару әдісі
168. ... – берілген процестерді зерттеу үшін физикалық пәні әр түрлі болады да, ұқсас математикалық өрнектермен бейнеленетін құбылыстарды қарастыру әдісі
А) математикалық модельдеу
Б) имитациялық модельдеу
В) статикалық модельдеу
Г) логикалық модельдеу
Д) транспорттық модельдеу
169. ... – әр түрлі объекттер мен жүйелердегі процестерді компьютердің көмегімен бейнеленетін және керекті көрсеткіштерін нақтылайтын әдіс
А) имитациялық модельдеу
Б) статикалық модельдеу
В) динамикалық модельдеу
Г) логикалық модельдеу
Д) стратегиялық модельдеу
170. ... – күрделі және бірімен бірі тығыз байланысты бірнеше объекттерден тұратын жүйелерді зерттеуге бейімделген әдіс
А) имитациялық модельдеу
Б) статикалық модельдеу
В) динамикалық модельдеу
Г) логикалық модельдеу
Д) стратегиялық модельдеу
171. Имитациялық модельдеу арқылы қандай басқару принциптерін орындауға болады?
А) бағалауға, таңдауға, болжауға
Б) сақтауға,жеткізуге,басқаруға
В) болжауға,бақылауға,орындауға
Г) қадағалауға,жеткізуге,басқаруға
172. Имитациялық модельдеудің кемшілігі -
А) шарттар мен параметрлердің мәніне тікелей байланыстылығы
Б) тиімділігі мен қабілеттерінің мәніне тікелей байланыстылығы
В) параметрлері мен қасиеттерінің мәніне тікелей байланыстылығы
Г) сапасы мен өлшемінің мәніне тікелей байланыстылығы
Д) көрсеткіштері мен сапасының мәніне тікелей байланыстылығы
173. Қор жинау кезінде көбінесе не қажет болады?
А) қорды толықтыру мөлшері және мезгілін анықтау
Б) қорды толықтыру сапасы мен көлемін анықтау
В) қорды толықтыру уақытын анықтау
Г) нақты бір жоспар болуы керек
Д) қорды толықтыру тиімділігі мен қасиеттерін анықтау
174. Жүйенің ретін анықтаңыз:
А) жабдықтаушы --- қойма --- тұтынушы
Б) тұтынушы---жабдықтаушы----қойма
В) қойма---жабдықтаушы
Г) жабдықтаушы---тұтынушы
Д) құрушы---жоспарлаушы
175. Рn нені анықтайды?
А) қойманың қорын бір рет толықтыруға жұмсалған қаржы
Б) кезекті күн
В) қордың бастапқы деңгейі
Г) модельдеу периодының ұзындығы
Д) бір тапсырыстың мөлшері
176. Модельдеу периодының ұзындығы қалай белгіленеді?
А) m
Б) p
В) c
Г) w
Д) e
177. Қойманың толық шығыны қалай белгіленеді?
А) УР
Б) УРх, УР, УР0
В) УР0
Г) УРх
Д) УР, УР0
178. і нені анықтайды?
А) кезекті тапсырыстың орындалатын күні
Б) бір тапсырыстың мөлшері
В) і-ші күнгі сұраныс
Г) шығындардың қосынды мәндері
Д) тапсырыс
179. n нені анықтайды?
А) кезекті күн
Б) тапсырыс
В) шығындардың қосындысы
Г) жұмыс жоспары
Д) өнім мөлшері
180. Қоймадағы қордың мөлшері
А) v
Б) m
В) n
Г) p
Д) i
181. Ұшақ пен кеме шайқасында қанша нәтиже болуы мүмкін?
А) 6
Б) 7
В) 9
Г) 5
Д) 8
182. Әуе шабуылының математикалық моделін құрастыру үшін мына параметрлер қолданылады:
А) U, W, M, N
Б) I, P, Y, T
В) X, Y, L, N
Г) V, Y, P, Pn
Д) D,M,D
183. t0= {(M-1)∆y егер Sy≥Sk
Sk-Sy/y +(M-1)∆y егер Sy<Sk формуласындағы SУ нені анықтайды
А) ҰР-ның шектік ұшу қашықтығы
Б) кеме мен ұшақтың аралығының қашықтығын
В) уақыт аралығы
Г) ұшақ пен кеменің қару комплектеріндегі ракеталар саны
Д) КР-ньщ шектік ұшу қашықтығы
184. Ұшақтың соңғы ракетасын алу моментінің формуласы:
А) t0= {(M-1)∆y егер Sy≥Sk
Sk-Sy/y +(M-1)∆y егер Sy<Sk
Б) R=Б[T/∆k]+1;
В)VPx=VPx+V*Px
Г)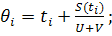 
Д)Vm ≤v
185. S(t)={Sy –V*t егер t<t0, Sy≥Sk
Sy-2V*t0+V*t егер t≥t, Sy≥Sk
Sk-2V*t0+V*t егер t≥t, Sy>Sk
Sy-2V0*t0+V*t егер t≥t0, Sy<Sk
формула нені анықтайды?
А) кеме мен ұшақтың аралығының қашықтығын
Б) уақыт аралығы
В) ұшақ пен кеменің қару комплектеріндегі ракеталар саны
Г) ұшақтың ұшу жылдамдығы
Д) ұР-ның шектік ұшу қашықтығы
186. Ұшақтың кеме зонасында өткізген уақытының формуласы
А) t={2[(Sk-Sy)/V+(M-1)∆y] , егер Sk>Sy
2[(M-1) ∆y-(Sk-Sy)/V ] , егер Sk≤Sy
Б) R=Б[T/∆k]+1;
В)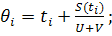
Г) VPx=VPx+V*Px
Д) Vm ≤v
187. R=Б[T/∆k]+1 қандай формула?
А) кеменің атып үлгіретін ракеталар саны
Б) ұшақтың ракетаны алу моменті
В) кеменің ракетаны алу моменті
Г) кеме мен ұшақ аралығының қашықтығы
Д) ұшақтың кеме зонасында өткізген уақыты
188. 1-ші жағдай. Кеменің j-ші ракетасын атқан уақытта ұшақ кемегеқарай ұшып келе жатса (τj<tc), бұл ракетаның ұшаққа жететін η j моменті мына теңдеуден анықталады:
А) η j- τj-S (η j)/(W+V)=0
Б) VPx=VPx+V*Px
В) R=Б[T/∆k]+1;
Г)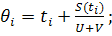
Д)VPx=VPx+V*Px
189. 2-ші жағдай. Кеменің j -ші ракетасын атқан уақытта ұшақ кейін карай ұшып бара жатса (τj>tc), η j моментін анықтау үшін келесі теңдеуді шешу керек:
А) η j- τj-S (η j)/(W-V)=0
Б) VPx=VPx+V*Px
В) R=Б[T/∆k]+1;
Г)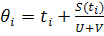 
Д)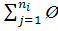 
190. t0= {(M-1)∆y егер Sy≥Sk
Sk-Sy/y +(M-1)∆y егер Sy<Sk
формуласындағы Sк нені анықтайды
А) КР-ньщ шектік ұшу қашықтығы
Б) ҰР-ның кемеге жету моменті
В) ұшақтың кеме зонасында өткізген уақыты
Г) кеме мен ұшақ аралығының қашықтығы
Д) кеменің атып үлгіретін ракеталар саны
191. t0= {(i-1)∆y егер Sy≥Sk
Sk-Sy/y +(i-1)∆y егер Sy<Sk
қандай формула?
А) ұшақтың і-ракетасын алу моменті
Б) кеме мен ұшақ аралығының қашықтығы
В) ұшақтың кеме зонасында өткізген уақыты
Г) ракетаны алу уақыты
Д) ұшақтың ұшу жылдамдығы
192. 
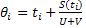қандай формула?
А) і-ші ҰР-ның кемеге жету моменті
Б) ұшақтың ұшу жылдамдығы
В) кезекті тапсырыстың орындалу күні
Г) і-ші күнгі сұраныс
Д) уақыт аралығын
193. τi= { Sk-Sy/y +(j-1)∆k егер Sy≥Sk
(j-1)∆k егер Sy<Sk
қандай формула?
А) кеменің j-ші ракетасын алу моменті
Б) і-ші күнгі сұраныс
В) кезекті тапсырыстың орындалу күні
Г) ұшақтың і-ракетасын алу моменті
Д) ееме мен ұшақ аралығының қашықтығы
194. P1(Si) нені анықтайды?
А) ұшақтың і-ракетасымен S, қашықтығындағы кеменің зақымдалмау ықтималдығы
Б) і-ші ҰР-ның кемеге жету моменті
В) КР-ньщ шектік ұшу қашықтығы
Г) кеменің атып үлгіретін ракеталар саны
Д) кеме мен ұшақ аралығының қашықтығы
195. Pк(Si) нені анықтайды?
А) кеменің і- ракетасымен ұшақтың жойылу ықтималдығы
Б) і-ші ҰР-ның кемеге жету моменті
В) кеменің атып үлгіретін ракеталар саны