Линейные дифференциальные уравнения

второго порядка (ЛДУ−II)

ЛДУ−II называется уравнение вида: у²+Р(x)у¢+Q(x)у=R(x), где функции Р(х), Q(x), R(x) не зависят от х.

Если R(x)=0, то уравнение называется уравнением без правой части или однородным ЛОДУ−II.

Если R(x)≠0, то уравнение называется уравнением с правой части или неоднородным ЛНДУ−II.

ЛОДУ−II с постоянными коэффициентами.

ау²+bу¢+cу=0, где а, b, c – некоторые постоянные.

Составим характеристическое уравнение аk²+bk+c=0, которое в зависимости от D может иметь различные решения.

· если D>0, то аk²+bk+c=0 имеет два различных действительных корня k₁ и k₂, тогда ЛОДУ−II имеет общее решение вида:

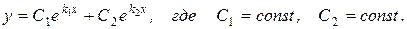
· если D=0, то аk²+bk+c=0 имеет два совпавших действительных корня k₁=k₂=k, тогда ЛОДУ−II имеет общее решение вида:

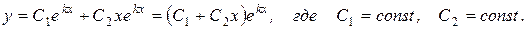
· если D<0, то аk²+bk+c=0 имеет два различных комплексных корня k_1,2=a±bi, тогда ЛОДУ−II имеет общее решение вида:

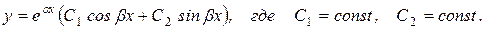
ЛНДУ−II с постоянными коэффициентами.

ау²+bу¢+cу=R(x), где а, b, c – некоторые постоянные.

Его общее решение имеет вид: 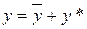, где

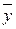- общее решение ЛОДУ−II ау²+bу¢+cу=0;

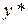- частное решение ЛНДУ−II ау²+bу¢+cу=R(x), которое ищется, в зависимости от правой части по одному из правил.

Правило 1: если правая часть R(x)=Р(х)е^kx, где Р(х) – какой-либо многочлен степени m, и если:

· k – не является корнем характеристического уравнения аk²+bk+c=0, то у*=Q(х)е^kx, где Q(х) – некоторый многочлен той же степени m, определяемый по методу неопределённых коэффициентов.

· k – является однократным корнем характеристического уравнения (то есть один из неравных корней D>0) аk²+bk+c=0, то у*=хQ(х)е^kx, где Q(х) – некоторый многочлен той же степени m, определяемый по методу неопределённых коэффициентов.

· k – является двукратным корнем характеристического уравнения (то есть один из равных корней D=0) аk²+bk+c=0, то у*=х²Q(х)е^kx, где Q(х) – некоторый многочлен той же степени m, определяемый по методу неопределённых коэффициентов.

Замечание 1: Если множитель Р(х) – есть постоянная величина (многочлен нулевой степени), то Q(x) – тоже постоянная величина (многочлен нулевой степени).

Замечание 2: Если множитель R(х) –многочлен, то есть k=0, то y* тоже многочлен.

Правило 2: если правая часть R(x)=е^ax(P₁(x)cosbx+P₂(x)sinbx) где P₁(x) и P₂(x) –многочлены соответственно степеней m₁ и m₂, и если:

· комплексные числа a±bi – не является корнями характеристического уравнения аk²+bk+c=0, то у*=е^ax(Q₁(x)cosbx+Q₂(x)sinbx), где Q₁(x) и Q₂(x) –многочлены, степени которых не превышают старшей из степеней m₁ и m₂.

· комплексные числа a±bi – является корнями характеристического уравнения аk²+bk+c=0, то у*=хе^ax(Q₁(x)cosbx+Q₂(x)sinbx), где Q₁(x) и Q₂(x) –многочлены, степени которых не превышают старшей из степеней m₁ и m₂.

Виды многочленов:

Многочлен n-ой степени	А0хn+А1хn-1+…+Аn-2х2+Аn-1х+Аn или Ахn+Вхn-1+…+Uх2+Vх+W	Примеры
Многочлен четвёртой степени	Ах4+Вх3+Сх2+Dх+E	х4-2х3+3х2+8, где А=1; В=-2; С=3; D=0; E=8;
Многочлен третьей степени	Ах3+Вх2+Сх+D	2х3-х2+4х, где А=2; В=-1; С=4; D=0;
Многочлен второй степени	Ах2+Вх+С	-х2+4х-3, где А=-1; В=4; С=-3;
Многочлен первой степени	Ах+В	х+8, где А=1; В=8;
Многочлен нулевой степени	А	1, где А=1.

[1] Квантор – от лат. quantum – сколько.

[2] Символ " есть перевёрнутая буква А, которая является начальной буквой английского слова All - все.

[3] Символ $ есть перевёрнутая буква $, которая является начальной буквой английского слова Exist - существовать.