Все вычисления выполняются с использованием программы обработки электронных таблиц MS Excel.

На основе статистических данных объема предложения (показатель Y) и цены товара (фактор X) оценить неизвестные параметры парной линейной регрессии, выполнить статистический и содержательный анализ оцененного уравнения регрессии, по полученной модели сделать прогноз и оценить точность этого прогноза.

Все вычисления выполняются с использованием программы обработки электронных таблиц MS Excel.

Задание выполняется в следующей последовательности.

1.По результатам наблюдений на корреляционном поле построить эмпирическую линию регрессии.

2.Выбрать форму связи между показателем Y и фактором X и составить уравнение регрессии.

3.Оценить параметры уравнения регрессии методом наименьших квадратов по исходным формулам.

4.На корреляционном поле кроме эмпирической линии регрессии построить теоретическую линию регрессии.

5.Построить:

- график изменения остатков регрессии;

- график изменения квадратов остатков регрессии;

- график изменения коэффициента эластичности предложения товара по цене товара.

6.Оценить тесноту связи между переменными Y и X:

- с помощью коэффициента корреляции;

- с помощью коэффициента детерминации;

- с помощью корреляционного отношения.

7.Проверить построенную регрессионную модель на адекватность по F-критерию Фишера с надежностью 0,95.

8.Оценить дисперсии оценок параметров регрессии.

9.Используя Т-тест Стьюдента, с надежностью 0,95 проверить статистическую значимость оценок параметров регрессии.

10.Определить доверительные интервалы для параметров регрессии.

11.Рассчитать точечную оценку прогноза показателя Y при прогнозном значении фактора .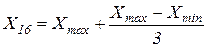

12.Рассчитать для прогноза точечную оценку коэффициента эластичности.

13.С надежностью 0,95 оценить доверительную зону базисных данных и доверительный интервал для прогнозного значения Y.

14.Построить в единой системе координат для базисных данных и прогноза теоретическую линию регрессии и доверительную зону регрессии.

15.Выполнить экономико-математический анализ основных экономических характеристик выявленной связи и дать им экономическое толкование. По полученным результатам сделать выводы.

16.Для тех же исходных данных выполнить построение линейной эконометрической модели методом наименьших квадратов с использованием встроенной статистической функции ЛИНЕЙН пакета MS Excel.

17.Для тех же исходных данных выполнить построение линейной эконометрической модели методом наименьших квадратов с помощью инструмента Анализа Данных «Регрессия» пакета MS Excel.

Исходные данные приведены в табл.1.1 и табл.1.2.

Таблица 1.1 – Результаты наблюдений Х (цена на товар, грн./шт.)

Номер наблюдения	Номер варианта
	6,5	10,1	2,1	2,5	2,2	3,7	3,2	2,2	4,6	2,3	6,2	1,9	2,1	3,1	2,0
	6,7	5,5	2,6	3,5	2,9	3,8	3,9	2,7	5,4	3,0	5,7	1,9	3,2	3,2	2,5
	7,5	7,0	3,1	3,8	3,3	3,8	5,0	3,5	5,3	2,2	7,5	2,1	3,0	3,9	3,0
	9,1	7,0	3,5	3,8	4,1	5,2	5,1	3,2	6,3	2,7	6,9	3,4	3,4	4,8	3,5
	9,2	7,6	4,2	4,2	5,3	5,0	6,0	3,9	7,6	3,7	8,3	4,0	5,2	4,6	4,0
	14,2	8,0	5,1	6,5	5,8	5,6	6,9	5,3	7,7	4,8	9,4	5,1	6,5	6,1	5,0
	9,9	8,6	4,8	4,8	4,9	5,5	7,3	4,6	7,5	4,6	8,3	4,3	5,7	4,9	4,5
	10,5	9,0	7,1	8,2	8,1	7,2	8,1	7,0	10,1	6,3	11,1	6,5	6,8	8,0	7,0
	11,0	5,1	5,7	5,8	5,9	7,0	7,5	5,9	8,4	5,3	9,7	5,5	6,4	7,1	5,5
	11,6	11,1	6,0	6,4	7,0	6,9	7,9	6,2	9,5	5,5	9,3	6,0	6,7	6,2	6,0
	12,0	12,0	6,7	7,7	7,0	8,0	8,4	6,4	9,2	6,0	10,5	6,2	7,5	6,8	6,5
	12,5	12,1	9,0	9,9	9,1	10,7	10,6	9,2	11,1	9,2	13,1	8,8	9,7	9,8	9,0
	12,7	12,6	7,5	7,7	8,1	9,3	8,8	7,3	9,9	6,8	11,5	6,1	6,3	8,3	7,5
	13,1	14,1	8,0	9,3	8,6	8,5	9,7	7,8	10,9	8,2	12,4	6,7	8,2	9,4	8,0
	9,3	15,0	8,6	9,3	9,5	10,3	10,3	8,5	11,9	8,5	12,4	7,2	7,2	9,0	8,5

Продолжение таблицы 1.1

Номер наблюдения	Номер варианта
	25,0	27,4	2,1	2,4	2,5	3,5	5,5	6,1	8,0	9,7	11,2	11,7	12,2	12,8	13,0
	28,8	35,6	4,5	4,3	4,2	4,8	8,7	8,8	12,3	13,5	13,8	13,9	14,0	18,1	15,5
	31,8	61,0	3,8	2,8	2,8	4,5	6,5	6,4	9,8	11,6	12,5	12,1	12,5	14,6	13,4
	49,1	43,2	4,2	4,0	4,1	4,8	7,5	7,6	11,7	12,6	13,3	12,7	13,4	16,3	14,3
	39,7	47,8	6,0	7,6	8,2	6,5	11,9	11,7	15,1	16,4	16,0	16,2	17,8	22,3	17,0
	43,8	54,0	5,6	4,9	4,6	4,9	10,6	10,2	13,9	15,3	13,8	15,2	14,5	18,9	15,5
	45,0	77,2	5,9	6,4	6,2	5,3	11,8	11,5	14,9	16,3	14,7	15,9	15,9	20,3	16,9
	48,6	37,4	6,6	9,2	11,1	10,0	13,0	12,8	16,1	18,8	17,9	17,8	21,1	23,7	19,5
	37,0	65,2	6,1	8,0	10,1	8,1	12,2	12,1	15,2	18,0	17,4	16,9	19,6	23,0	17,8
	73,9	68,8	10,6	14,6	16,1	13,5	19,0	16,2	20,8	23,6	22,0	23,7	29,2	28,6	23,9
	52,9	71,0	6,8	10,4	12,1	11,4	14,1	13,0	17,8	19,6	19,0	17,9	22,9	24,7	19,5
	56,5	59,4	7,6	10,8	13,6	12,1	15,1	13,0	18,6	19,9	20,8	18,7	24,7	25,8	20,9
	63,2	79,6	9,3	10,8	14,1	12,6	16,8	14,4	19,0	21,7	20,9	20,4	26,4	26,6	22,8
	70,1	80,0	9,9	12,7	15,5	12,7	17,6	16,2	20,4	22,1	20,9	22,1	28,4	28,6	23,0
	50,2	91,4	12,5	16,6	17,0	15,4	20,3	17,5	22,5	23,9	23,8	24,7	30,6	28,8	24,0

Таблица 1.2 – Результаты наблюдений Y (объем предложения, тыс.грн.)

Номер наблюдения	Номер варианта
	6,6	5,1	7,2	10,9	16,2	12,1	15,2	16,6	10,2	12,5	19,7	14,9	22,7	10,7	4,3
	6,4	3,1	8,0	11,9	17,8	12,3	15,4	17,6	10,6	13,9	20,5	15,8	23,9	11,9	9,5
	7,4	3,3	9,3	12,5	18,4	13,8	16,4	19,2	12,0	15,2	21,3	16,8	24,3	13,0	9,1
	6,7	3,6	10,1	13,3	18,9	14,8	17,9	19,4	12,8	16,1	22,6	18,0	26,0	13,4	13,0
	7,3	3,8	11,1	14,1	19,6	15,9	18,5	20,5	13,3	16,7	23,3	18,3	26,2	15,1	13,1
	11,0	4,0	13,0	16,1	21,8	17,8	20,8	22,5	15,8	18,5	25,9	20,3	28,1	16,3	18,4
	9,8	4,2	12,2	15,2	21,2	16,4	19,8	22,0	15,1	17,7	24,4	19,9	27,6	16,0	16,1
	8,7	4,8	17,0	20,5	25,5	21,1	24,2	26,1	19,5	22,2	29,2	24,1	32,3	20,5	25,3
	8,4	2,5	14,1	17,4	23,0	18,6	21,3	23,6	17,1	19,5	26,7	21,2	29,8	18,1	18,5
	9,3	5,3	15,2	18,7	24,4	19,6	22,3	24,9	18,0	20,6	27,4	22,5	30,3	18,4	20,2
	9,5	5,9	16,3	19,5	25,4	21,3	24,1	25,5	18,3	21,8	28,4	23,5	31,5	19,5	24,1
	9,5	6,0	21,2	25,0	30,8	25,4	29,0	30,4	24,2	27,2	33,7	28,4	37,0	24,4	34,0
	9,9	6,5	18,0	21,3	27,1	23,0	25,7	28,0	20,6	23,8	30,5	25,6	33,8	21,7	26,7
	10,1	6,8	19,2	22,6	28,0	23,4	26,5	28,4	21,4	24,8	31,2	27,1	34,7	23,2	29,9
	9,3	7,0	20,2	23,7	29,0	24,6	27,5	29,5	23,2	25,6	32,6	27,6	35,9	23,6	30,5

Продолжение таблицы 1.2

Номер наблюдения	Номер варианта
	10,1	1,4	10,2	12,5	19,7	14,9	22,7	10,7	4,3	7,2	10,9	16,2	12,1	15,2	16,6
	11,1	1,7	12,8	16,1	22,6	18,0	26,0	13,4	13,0	10,1	13,3	18,9	14,8	17,9	19,4
	12,3	3,2	10,6	13,9	20,5	15,8	23,9	11,9	9,5	8,0	11,9	17,8	12,3	15,4	17,6
	19,8	2,2	12,0	15,2	21,3	16,8	24,3	13,0	9,1	9,3	12,5	18,4	13,8	16,4	19,2
	15,8	2,3	15,8	18,5	25,9	20,3	28,1	16,3	18,4	13,0	16,1	21,8	17,8	20,8	22,5
	17,2	2,7	13,3	16,7	23,3	18,3	26,2	15,1	13,1	11,1	14,1	19,6	15,9	18,5	20,5
	18,1	3,8	15,1	17,7	24,4	19,9	27,6	16,0	16,1	12,2	15,2	21,2	16,4	19,8	22,0
	19,2	1,9	18,0	20,6	27,4	22,5	30,3	18,4	20,2	15,2	18,7	24,4	19,6	22,3	24,9
	15,2	3,4	17,1	19,5	26,7	21,2	29,8	18,1	18,5	14,1	17,4	23,0	18,6	21,3	23,6
	29,5	3,4	23,2	25,6	32,6	27,6	35,9	23,6	30,5	20,2	23,7	29,0	24,6	27,5	29,5
	21,1	3,7	18,3	21,8	28,4	23,5	31,5	19,5	24,1	16,3	19,5	25,4	21,3	24,1	25,5
	22,6	2,9	19,5	22,2	29,2	24,1	32,3	20,5	25,3	17,0	20,5	25,5	21,1	24,2	26,1
	25,4	4,0	20,6	23,8	30,5	25,6	33,8	21,7	26,7	18,0	21,3	27,1	23,0	25,7	28,0
	28,1	4,0	21,4	24,8	31,2	27,1	34,7	23,2	29,9	19,2	22,6	28,0	23,4	26,5	28,4
	20,2	4,5	24,2	27,2	33,7	28,4	37,0	24,4	34,0	21,2	25,0	30,8	25,4	29,0	30,4

Методические рекомендации

Регрессионная модель называется линейной, если она линейна по своим переменным и параметрам. Парные линейные регрессионные модели устанавливают линейную зависимость между двумя переменными. При этом одна из переменных считается объясняемой переменной (в данной работе – Y) и рассматривается как функция от объясняющей переменной (в данной работе – X).

1.Эмпирическую линию регрессии при парной корреляции получают следующим образом.

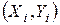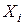Данные наблюдений располагают в порядке возрастания значений Х и на точечный график, называемый корреляционным полем, наносят точки с координатами , где и 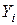– соответственно наблюдаемые значения объясняющей и объясняемой переменных в i‑том наблюдении. Для быстрой сортировки списка, содержащего выделенные ячейки данных наблюдений, по возрастанию Х, нажмите кнопку «Сортировать по возрастанию» на панели инструментов «Стандартная».

Если при одном и том же значении 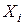наблюдалось несколько значений Y, необходимо (только для построения эмпирической линии регрессии!) вычислить групповое среднее из этих Y.

Соединив точки групповых средних в порядке возрастания Х отрезками прямой, получим эмпирическую (наблюдаемую) линию регрессии. По ее характеру и расположению можно сделать предварительный вывод о форме корреляционной связи.

2.Уравнение регрессии – это аналитическое выражение, с помощью которого описывается функциональная составляющая связи между переменными. Сделав допущение о линейной связи между Y и X, уравнение регрессии будет иметь вид

,

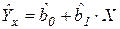где

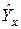- оценка (расчетное значение) показателя Y;

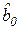- оценка истинного значения постоянного коэффициента (свободного члена);

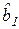- оценка коэффициента регрессии, имеющего смысл относительного прироста.

Отклонения расчетных значений от наблюдаемых значений дают остатки регрессии:

,

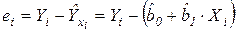где

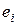- отклонения расчетных значений от наблюдаемых значений;

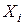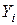, - значения переменных в i-том наблюдении;

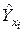- расчетное (оцененное) значение Y, определенное по уравнению регрессии при наблюдаемом значении .

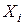3.Для нахождения оценок параметров уравнения регресси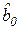и ( и 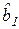) используют метод наименьших квадратов, состоящий в минимизации выражения

.

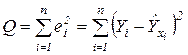После нахождения частных производных Q по оценкам 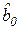и 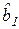и приравнивании их нулю получим систему нормальных уравнений, решив которую найдем:

;

,

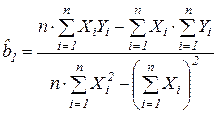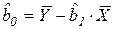где

n - число наблюдений (в данном задании n=15);

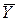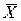, - средние значения соответственно Y и X для данного массива наблюдений

, .

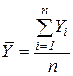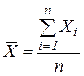Расчеты рекомендуется выполнять в форме табл.1.3. При этом следует обратить внимание на обязательное выполнение (с точностью до вычислительной ошибки!) проверочных услови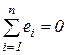й: и .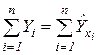

Вычислив оценк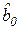и и 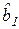, составьте искомое уравнение регрессии в явном виде и объясните, как изменится показатель Y при изменении фактора X на единицу.

Таблица 1.3 – Данные для расчета параметров уравнения регрессии и анализа качества модели

i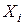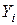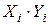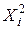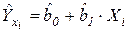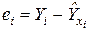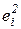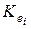
...
n
Σ								-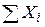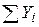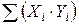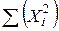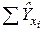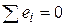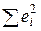
Σ/n			-	-	-	-	-	-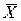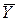

Продолжение таблицы 1.3

i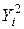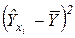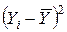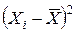
...
n
Σ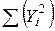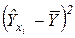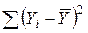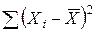
Σ/n	-			-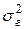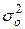

4.На точечном графике, где ранее была построена эмпирическая линия регрессии, постройте теоретическую линию регрессии (по расчетным значениям 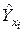при наблюдаемых значениях ).

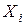5.Постройте следующие графические зависимости:

- график изменения остатков регрессии ;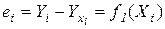

- график изменения квадратов остатков регрессии ;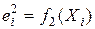

- график изменения точечной оценки коэффициента эластичности предложения товара по его цене

.

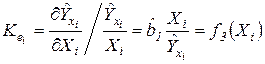Коэффициент эластичности показывает, на сколько процентов изменится показатель Y при изменении фактора X на 1%.

6.Для оценки тесноты и направления линейной связи между Y и X используется коэффициент корреляции:

.

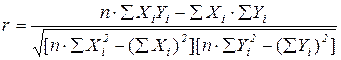Для оценки тесноты связи при любой форме связи между Y и X используется корреляционное отношение:

,

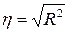где

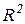- коэффициент детерминации, показывающий долю общей колеблемости Y, которая объясняется колеблемостью фактора X:

;

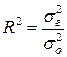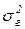- межгрупповая дисперсия, отражающая влияние только учтенных факторов (в данном случае – X) на колеблемость Y:

;

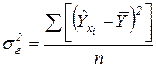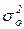- общая дисперсия, отражающая влияние всех факторов (как учтенных, так и не учтенных) на колеблемость Y:

.

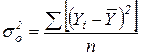Проверить выполнения равенства 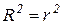, имеющего место для случая парной линейной регрессии.

Данные для расчета представлены в табл.1.3.

7.Проверка модели на адекватность по F-критерию Фишера позволяет оценить статистическую значимость коэффициента детерминации .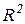

Она выполняется в несколько этапов.

Этап 1. Определяем расчетное значение F-статистики по формуле:

,

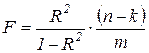где

n - размер выборки (количество наблюдений). В данном задании n=15;

k - число оценённых параметров (в нашей модели k=2, т.к. мы оценивали два параметра: 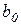и );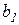

m - число объясняющих переменных (в нашей модели m=1).

Из этого соотношения следует, что малым значениям F-статистики (отсутствие значимой функциональной связи Y и X) соответствуют малые значения 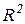(плохая аппроксимация данных).

Этап 2. Задаем уровень значимости 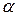(или уровень ошибки ).

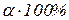Например, если мы считаем, что возможная ошибка для нас составляет 5%, это означает, что мы можем ошибиться не больше, чем в 5% случаев, а в 95% случаев (или в 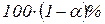) наши выводы будут правильными.

Пусть уровень значимости 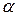=0,05, т.е. допускаем 5%-ный риск ошибиться.

Этап 3. По статистическим таблицам F-распределения Фишера для 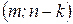степеней свободы и уровня доверия 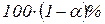находим критическое значение .

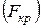В данном случае при n=15 по статистическим таблицам F-распределения Фишера для 5%-ного уровня значимости 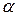и степеней свободы соответственно 1 и n-2=15-2=13 критическое значение .

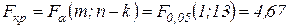Этап 4. Если 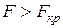, то построенная регрессионная модель с риском ошибиться не больше, чем в 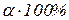случаях, адекватна реальной действительности, и в этом случае можно сделать вывод об адекватности принятой модели статистическим данным по F‑критерию Фишера.

Малые значения F-статистики, когда 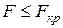, говорят об отсутствии значимой функциональной связи Y и X.

8.Оценки дисперсии оценок параметров регрессии рассчитываются по формулам:

;

,

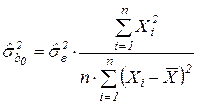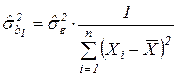где

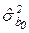- оценка дисперсии оценки ;

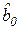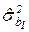- оценка дисперсии оценки ;

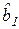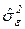- несмещенная оценка дисперсии ошибок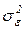

.

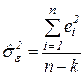Данные для расчета представлены в табл.1.3.

9.Значимость оценок параметров регрессии, определенных методом наименьших квадратов, проверяется с помощью Т-теста Стьюдента.

Для оценки каждого i-того параметра рассчитывается t-статистика:

,

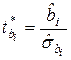где

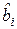- оценка параметра 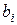, полученная методом наименьших квадратов;

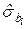- оценка стандартной ошибки (оценка стандартного отклонения) оценки параметра .

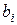В нашей модели оценивалось два параметра. Поэтому необходимо рассчитать две t статистики – для оценки параметра 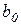и для оценки параметра :

; .

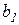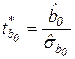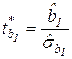Значение каждой t-статистики сравнивается с табличным критическим значением 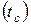, которое определяется по таблицам t-распределения Стьюдента при заданной доверительной вероятности и степенях свободы .

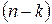В данном случае при доверительной вероятности 0,95 и степенях свободы
n-k=15-2=13 критическое значение: .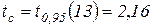

Если 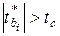, делается вывод о том, что с заданной вероятностью оценка 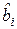является статистически значимой, т.е. оценка параметра статистически достоверно отличается от нуля.

В противном случае, делается вывод о том, что с заданной вероятностью оценка 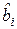является статистически незначимой.

10.Доверительные интервалы для параметров регрессионной модели – это такие интервалы, в которые с заданной вероятностью (в данном случае с вероятностью 0,95) попадают истинные значения параметров регрессии.

Доверительные интервалы для параметров позволяют связать оценки параметров с их истинными значениями и рассчитываются по формулам:

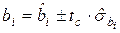
или

.

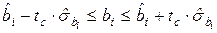11.Если построенная эконометрическая модель адекватна статистическим данным, то мы можем, исходя из этой модели, находить прогнозные значения зависимой переменной Y.

Точечный прогноз дает значение оценки 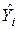зависимой переменной для соответствующего значения 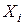по построенной модели:

.

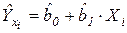12.Точечная оценка коэффициента эластичности для прогноза:

.

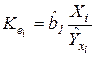13.Доверительный интервал для математического ожидания 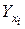при заданном доверительном уровне имеет вид:

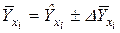
или

,

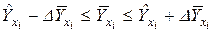где

.

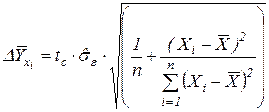Обратите внимание, что здесь n – это размер выборки (количество наблюдений). В данном задании n=15.

Как видно из последней формулы, доверительный интервал среднего значения прогноза минимальный, если 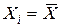, и увеличивается нелинейно по мере того, как 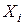удаляется от своего среднего по выборке значения.

14.Для наглядного представления расчетов постройте диаграмму, содержащую следующие графические зависимости:

- теоретическую линию регрессии для базисных данных (результатов наблюдений) и прогноза;

- доверительную зону 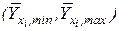для базисных (наблюдаемых) данных и прогноза:

;

.

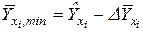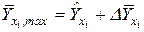Расчеты рекомендуется выполнять в форме табл.1.4.

Таблица 1.4 – Данные для расчета прогноза

i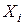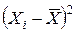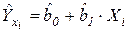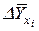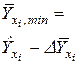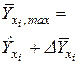
...
n=15
Σ				-	-	-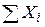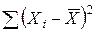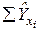
Σ/n		-	-	-	-	-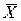

15.Выводы по работе формулируются по следующей схеме:

- поскольку 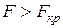, то с надежностью ... построенную регрессионную модель ... можно считать адекватной наблюдаемым данным и на основе этой модели можно проводить экономический анализ;

- при изменении фактора X на единицу показатель Y изменится на ... единиц;

- значение коэффициента эластичности при изменении фактора от 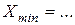до 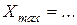изменяется от ... до ...;

- для прогнозного значения фактора 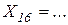среднее значение прогноза показателя 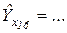с надежностью ... будет находиться в пределах от ... до ...;

- для прогнозного значения фактора 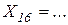среднее значение коэффициента эластичности равно ... . Это означает, что при изменении фактора на 1% показатель изменится на ...%;

- коэффициент корреляции равен ..., что говорит о тесной линейной связи фактора и показателя.

16.Встроенная статистическая функция ЛИНЕЙН пакета MS Excel определяет методом наименьших квадратов оценки параметров линейной регрессии вида (обратите внимание на порядок расположения объясняющих переменных и оценок параметров):

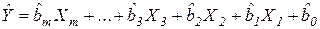
Порядок действий:

1) выделите область пустых ячеек, состоящую из 5 строк и (m+1) столбцов (где m – количество объясняющих переменных) для вывода результатов регрессионной статистики;

2) активизируйте Мастер функций одним из способов:

· в главном меню выберите Вставка/Функция;

· на панели инструментов Стандартная щелкните по кнопке Вставка функции ;

3) в раскрывшемся окне выберите Категорию Статистические, Функцию – ЛИНЕЙН. Щелкните по кнопке ОК;

4) заполните аргументы функции:

· Известные_значения_y – диапазон, содержащий данные, характеризующие результативный признак;

· Известные_значения_x – диапазон, содержащий данные, описывающие все объясняющие переменные;

· Константа – логическое значение, указывающее на наличие или отсутствие свободного члена в уравнении регрессии; если Константа = 1, то свободный член 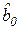рассчитывается обычным образом, если Константа = 0, то свободный член 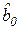полагается равным 0, и значения остальных параметров подбираются так, чтобы выполнялось соотношение:

;

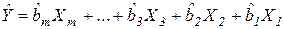· Статистика – логическое значение, которое указывает, выводить дополнительную статистику по регрессии или нет. Если Статистика = 1, то дополнительная информация по регрессионному анализу выводится, если Статистика = 0, то выводятся только оценки параметров уравнения регрессии;

5) Щелкните по кнопке ОК. В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу F2, а затем – на комбинацию клавиш Ctrl+Shift+Enter.

Структура массива дополнительной регрессионной статистики представлена в табл.1.5.

Таблица 1.5 – Массив регрессионной статистики, формируемый функцией ЛИНЕЙН

		. . .
		. . .
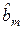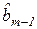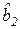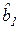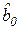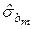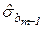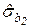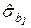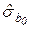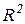	Стандартная ошибка модели (стандартная ошибка остатков)	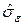#Н/Д	#Н/Д	#Н/Д	#Н/Д
F-статистика		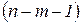#Н/Д	#Н/Д	#Н/Д	#Н/Д
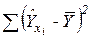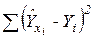		#Н/Д	#Н/Д	#Н/Д	#Н/Д

Для случая парной линейной регрессии результат применения функции ЛИНЕЙН выглядит следующим образом (пример):

1,145664	2,456743
0,037978	0,71512
0,985916	0,541232
910,0041
266,5692	3,808115

Таким образом, в этом примере получили следующее оцененное уравнение регрессии:

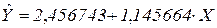
В отчете необходимо:

· привести массив регрессионной статистики, сформированный функцией ЛИНЕЙН для своих исходных данных и описать его содержимое;

· проанализировать массив регрессионной статистики путем сравнения его содержимого с результатами, полученными ранее непосредственно по исходным формулам;

· сформулировать достоинства и недостатки применения функции ЛИНЕЙН с точки зрения удобства анализа статистического качества линейной регрессионной модели.

17.Построение линейной эконометрической модели методом наименьших квадратов с помощью инструмента Анализа Данных «Регрессия» пакета MS Excel выполняется в следующем порядке:

1) проверьте доступ к Пакету анализа. При его отсутствии в главном меню выберите Сервис/Надстройки, установите флажок Пакет анализа, щелкните по кнопке ОК;

2) в главном меню выберитеСервис/Анализ данных/Регрессия.Щелкните по кнопке ОК;

3) заполните диалоговое окно Входные данные и Параметры вывода:

· Входной интервал Y – диапазон, содержащий данные результативного признака;

· Входной интервал Х – диапазон, содержащий данные независимых переменных;

· Метки – флажок, который указывает, содержит ли первая строка название столбцов или нет;

· Константа - ноль – флажок, указывающий на отсутствие или наличие свободного члена 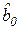в уравнении регрессии: если флажок установлен, то свободный член 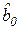полагается равным 0;

· Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;

· Новый рабочий лист – можно задать произвольное имя нового листа.

Если необходимо получить информацию об остатках и графики остатков, установите соответствующие флажки в диалоговом окне. Щелкните по кнопке ОК.

Результаты регрессионного анализа для линейной модели с двумя переменными при установленном флажке Остатки выглядят следующим образом (пример):