Основные теоретические положения. Метод контурных токов – один из основных и широко применяемых на практике методов
Метод контурных токов – один из основных и широко применяемых на практике методов. Для каждого контура цепи задают ток, который остается неизменным. В цепи протекает столько контурных токов, сколько независимых контуров в ней содержится. Направление контурного тока выбирают произвольно.
Контурные токи, проходя через узел, не меняют своего значения и направления. Следовательно, первый закон Кирхгофа выполняется автоматически. Уравнения с контурными токами записываются только для второго закона Кирхгофа. Число уравнений, составленных по методу контурных токов, меньше чем по методу законов Кирхгофа.
Число уравнений, составляемых по методу контурных токов, определяется по формуле:
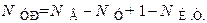 .
.
Если в цепи отсутствуют источники тока, число уравнений равно числу контурных токов и, соответственно, числу независимых контуров рассматриваемой электрической цепи.
Если заданная электрическая цепь содержит nнезависимых контуров, то на основании второго закона Кирхгофа получается nконтурных уравнений:
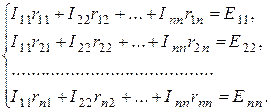 | (3.1) |
где 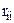 – собственное сопротивление контура, равное сумме сопротивлений, по которым протекает контурный ток
– собственное сопротивление контура, равное сумме сопротивлений, по которым протекает контурный ток 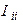 (
( 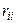 – величина положительная),
– величина положительная),
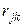 – взаимное сопротивление между двумя смежными контурами, которое может быть положительным или отрицательным в зависимости от того, совпадают ли направления протекающих по ним контурных токов,
– взаимное сопротивление между двумя смежными контурами, которое может быть положительным или отрицательным в зависимости от того, совпадают ли направления протекающих по ним контурных токов,
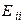 – контурная Э.Д.С., равная алгебраической сумме Э.Д.С., входящих в данный контур.
– контурная Э.Д.С., равная алгебраической сумме Э.Д.С., входящих в данный контур.
После решения системы (3.1) ток в ветви определяют как алгебраическую сумму контурных токов, протекающих через данную ветвь.
Примеры расчета линейных электрических цепей методом контурных токов
Пример 3.1
Составить уравнение по методу контурных токов и определить токи во всех ветвях схемы (рис. 3.1), если 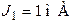 ;
; 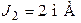 ;
; 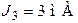 ;
; 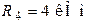 ;
; 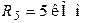 ;
; 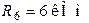 ;
; 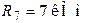 ;
; 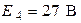 .
.
На примере данной задачи покажем как пользоваться методом контурных токов, если схема содержит источники тока.
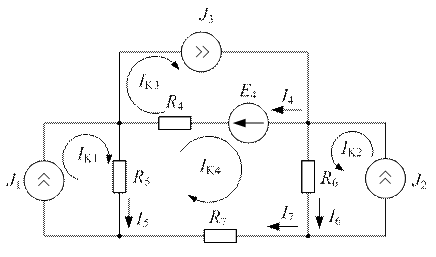 |
| Рис. 3.1 |
Решение
В цепи четыре независимых контура, следовательно обозначим четыре контурных тока: 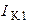 ,
, 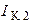 ,
, 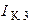 ,
, 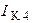 и их положительные направления.
и их положительные направления.
Токи 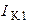 ,
, 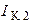 ,
, 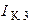 , протекают через источники тока
, протекают через источники тока 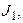
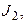
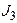 соответственно. Следовательно:
соответственно. Следовательно: 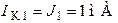 ;
; 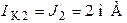 ;
; 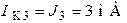 ;
;
В данной задаче необходимо определить один контурный ток 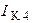 , следовательно, составим только одно уравнение:
, следовательно, составим только одно уравнение:
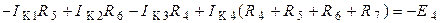 ,
,
Откуда 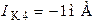 .
.
Токи ветвей определим как алгебраическую сумму контурных токов:
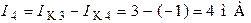 ;
;
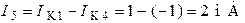 ;
;
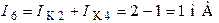 ;
;
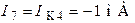 .
.
Правильность решения задачи проверим, составив уравнение по второму закону Кирхгофа для контура 4 (контур обходим по часовой стрелке):
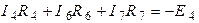 ;
;
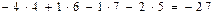 ;
;
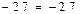 .
.
Второй закон Кирхгофа выполняется.
Ответ: 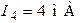 ,
, 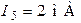 ,
, 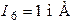 ,
, 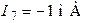 .
.
Пример 3.2
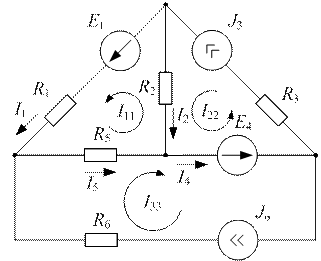 Рис. 3.2 Рис. 3.2 | Дано: 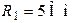 ; ; 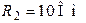 ; ; 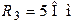 ; ; 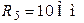 ; ; 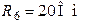 ; ; 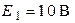 ; ; 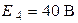 ; ; 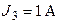 ; ; 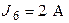 . Определить токи в схеме рис. 3.2 методом контурных токов. Решение Выбираем направления контурных токов. Контурные токи . Определить токи в схеме рис. 3.2 методом контурных токов. Решение Выбираем направления контурных токов. Контурные токи 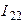 и и 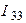 совпадают по направлению с токами источников совпадают по направлению с токами источников 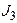 и и 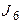 и равны им и равны им |
соответственно: 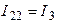 ;
; 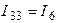 . Для решения задачи необходимо составить одно уравнение для неизвестного контурного тока
. Для решения задачи необходимо составить одно уравнение для неизвестного контурного тока 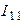 :
:
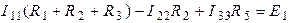 .
.
Решив его, получаем:
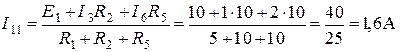 .
.
Токи в ветвях схемы определяем как алгебраическую сумму контурных токов, проходящих через каждую ветвь:
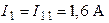 ;
;
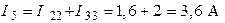 ;
;
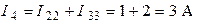 ;
;
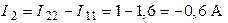 .
.
Ответ: 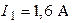 ,
, 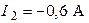 ,
, 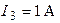 ,
, 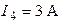 ,
, 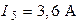 ,
, 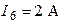 .
.
Метод узловых напряжений
