Список использованных источников. Пружина растягивается на Dx = 4 см под действием силы F = 50 H

ЗАДАЧА 10

Пружина растягивается на Dx = 4 см под действием силы F = 50 H. Определить потенциальную энергию W_п пружины, растянутой на Dx1 = 3см

Решение:

F=50H при Dx= 4см= 0,04мм. Dx1=3см=0,03мм

Потенциальную энергию силу определим следующим образом

W₁=к Dx²/2, W₂=к Dx₁²/2.

Энергия, которую получит пружина, равна разности, конечной (W₂) и начальной энергии

Dw=W2-W1= к Dx²/2- к Dx₁²/2.=к/2* Dx²- Dx₁²

Коэффициент упругости k определим по закону Гука F = − kΔx

Отсюда Dw=(F/2 Dx₁)* Dx²- Dx₁²=(50/2*0,03)*0,04-0,03=0,75*0,01=75 Дж

Задача 19

Материальная точка массой m=2 гр совершает колебания по закону x = 2sin πt. Определить потенциальную W_п и кинетическую W_к энергии точки в момент времени t = 1/3 с.

Решение:

M=2гр= 2 × 10⁻³кг

x = 2sin πt

t = 1/3 с.

Закон изменения кинетической энергии

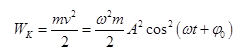
W_k=((π)²*2 × 10⁻³/2)*(1*10^-1)²*cos²(πt)= 3,24*10^-5 Дж

Закон изменения потенциальной энергии

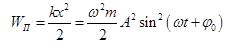
W_п=((π)²*2 × 10⁻³/2)*(1*10^-1)²*sin²(πt)= 9,78 × 10⁻⁸Дж

Задача 28

Кислород массой m = 250г, имевший температуру Т1 = 200К, был адиабатически сжат. При этом была совершена работа А = 25 кДж. Определить конечную температуру Т2 газа.

Решение:

A=-i/2*m/M*R(T1-T2)

При адиабатном процессе (Q=0) и работа совершенная над газом пошла на увеличение энергии дельдаU=A, ДельтаU = 5/2mR(T2-T1), где m=0,025кг/моль (множитель 5/2 – так как газ двух атомный).

Отсюда находим

Т2-Т1=2АМ/(5mR)=50*10³*0,025/(5*0,25*8,31)=5193,75/8,31=625К.

Значит Т2=Т1+625=1250К.

Задача 37

Определить молярную концентрацию {C} клеточного сока в клетках виноградных листьев при температуре окружающей среды t = 27 C. Диссоциацией молекул пренебречь. Осмотическое давление р считать равным 1,62 МПа.

Решение:

Осмотическое давление определяется формулой

P=CRT, где C – молярная концентрация раствора, моль/л

R - – универсальная газовая постоянная 8,314 Дж/(моль∙К)

T – абсолютная температура в Кельвинах

1^оС = 273 К, тогда 27^оС = 300 К.

P=1.62мПА =1,62*10⁶ ПА

Для растворов недиссоциированных молекул вещества

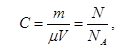
Где N_A постоянная Авогадро (6,02·10²³ моль⁻¹), N — число молекул растворенного вещества в единице объема раствора.

Число молекул растворенного вещества

N = PNA/RT = (1,62*10⁶ *6,02·10²³)/8.314*300=9.75*10²⁹/2494=3,91*10²⁶ молекул

С =N/ N_A=3,91*10²⁶/6,02·10²³=6,4 × 10⁴⁸ моль/л.

Задача 46

Определить величину двух одинаковых зарядов, находящихся на расстоянии r = 8 см друг от друга и взаимодействующих с силой F = 15.6 * 10^-5 H

Решение:

Закон Кулона для одинаковых зарядов Q F = kQ²/r² откуда
Q² = Fr²/k

k-постоянный коэффициент=9*10⁹ H
Q = r√(F/k) = 0.8√(15.6 * 10^-5/(9*10⁹)) = 1,1*10^-4 мкКл

Задача 55

Определить плотность тока i в железном проводе длиной I = 20м, подающем ток для зарядки тракторного аккумулятора. Провод находится под напряжением U = 12В. Удельное сопротивление железа р=1,2 * 10^-7 Ом*м.

Решение:

I=U/R

U=12B

R= р *L/S,

где L=20 м,

р - удельное сопротивление железа

S - площадь сечения проводника

i=I/S=U/( р *L) = 12/(1,2 * 10^-7*20)= 5 × 10⁶ А/м²

Задача 64

На прямолинейный проводник длиной l =45см, расположенный под углом а=30 к силовым линиям магнитного поля, действует сила F = 30 мН. Определить индукцию магнитного поля В, если сила тока в проводнике I=2a.

Решение:

A=30 гр.

L=45см

F=30mH

I=2 А

B-?

На проводник с током действует сила Ампера формула которой:

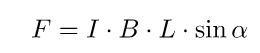
sin30=0,5

Откуда B=F/i*l*sina=30/2*45*sin30=0,6 мТл=60*10⁴ ТЛ

Задача 73

Источник тока замкнули на катушку с индуктивностью L = 0,4 Гн. Определить сопротивление R катушки, если сила тока I в катушке достигает 20% ее максимального значения за время Dt = 0,1 с после замыкания цепи.

Решение:

L=0.4 Гн

t= 0.1c

I = 20%I₀

Мгновенное значение силы тока в цепи, обладающей сопротивление R и индуктивностью L при замыкании цепи:

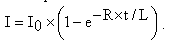
0.2I₀=I₀(I-e^-Rt/L)

0.2= I-e^-Rt/L

0.8= e^-Rt/L

-Rt/L=ln0.8

R=L*ln0.8/t

R=892 мОм

Задача 82

На грань кристалла каменной соли падает параллельный пучок рентгеновского излучения. Расстояние между атомными плоскостями кристалла d = 280 пм. Определить длину волны излучения, если дифракционный максимум первого порядка наблюдается под углом 65^о

Решение:

Из уравнения Брэгга-Вульфа 2d*sin0=nL, имеем L=2d*sin0/n

В нашем случае n=1 – первый порядок отражения, и 0=a.

Поэтому L= 2d*sina=2*280ПМ*sin65=507 ПМ=0,507 НМ

Задача 91

При прохождении поляризованного света через слой 5%-го сахарного раствора толщиной l₁ = 10см плоскость поляризации повернулась на угол ф1 = 3. Найти концентрацию С2 другого раствора сахара толщиной l₂ = 15 см, если плоскость поляризации повернулась при этом угол ф2 =5,4

Решение:

ф1 = 3

l₁ = 10см

С1=5%

ф2 =5,4

l₂ = 15 см

В случае раствора угол поворота плоскости колебаний света, проходящего через слой толщиной L, вещества концентрации С равен:

Ф=a*C*L. откуда ф1=a*C1*L1, поэтому a=ф1/C1*L1

С другой стороны ф2= a*C2*L2. Откуда концентрация равна

С2=ф2/a*L2=(ф2*L1/ф1*L2)*C1=(5.4*0.1мм/3*0,15мм)*5%=6

Список использованных источников

1. Грабовский Р. И. Курс физики – СПб.: Лань, 2009.

2. Дмитриева В. Ф. Физика: программа, метод. указания и контрольные задания для вузов/ В. Ф. Дмитриева, В. А. Рябов, В. М. Гладской. – 4-е изд., перераб. и доп. – М.: Высш. шк., 2007.