Лекция 2. Слабая (обобщенная) форма постановки краевых задач для дифференциальных уранений

М К Э

Лекция 1. Метод Галёркина

Об ортогональности функций

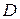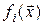Пусть ‑ область изменения , а ‑ функции, определенные в 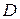. Через 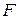обозначим класс этих функций.

а) Если 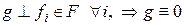. Обозначение: .

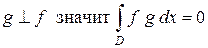б) Пусть 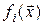‑ полная в 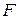система базисных функций. Тогда любая функция 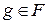представима в виде разложения по базису

,

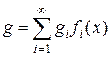где коэффициенты 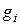определяются однозначно. Базисные функции линейно независимы, т.е. из равенства 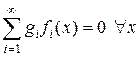следует, что все коэффициенты 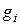равны нулю. Но тогда и 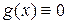. Итак, если функция ортогональна системе базисных функций, то она тождественно равна нулю.

Метод взвешенных невязок

Рассмотрим уравнение

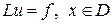. (1.1)

Пусть 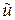‑ приближение к решению 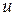уравнения (1). Обозначим через

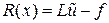(1.2)

невязку уравнения (1) на этом приближенном решении. Пусть, далее, 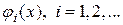‑ система базисных функций. Тогда можно записать

.

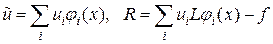Чтобы найти коэффициенты 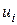, потребуем, чтобы невязка 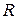была ортогональна некоторой системе весовых функций 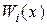, т.е.

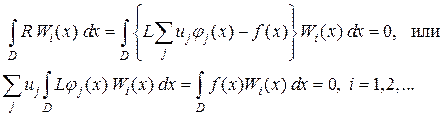(1.3)

Метод Галеркина

Галеркин использовал базисные функции вместо весовых, что приводит к следующей системе линейных уравнений относительно искомых коэффициентов разложения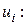

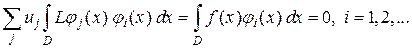
или

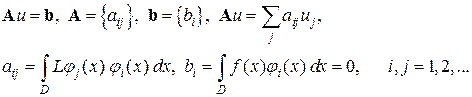(1.4)

Замечание. В конечномерном пространстве 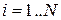, и система уравнений (4) становится конечной.

Пример применения метода Галеркина.

Решим задачу

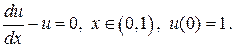(1.5)

Точное решение этой задачи очевидно: 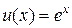. Выберем систему базисных функций

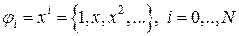(1.6)

и запишем решение в виде разложения по базису,

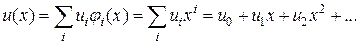. (1.7)

В разложении (7) искомыми являются коффициенты 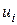. Полагая 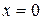, находим 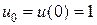. Пусть 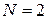, тогда осталось найти 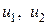. Подставим (7) в (5) и вычислим невязку

.

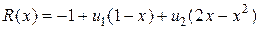Потребуем 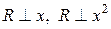. Получим систему уравнений

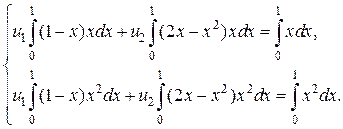
Вычислим интегралы и получим

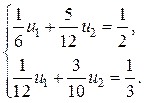
Решение этой системы таково: 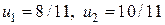, а приближенное решение (7) задачи (5) есть парабола

.

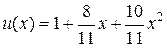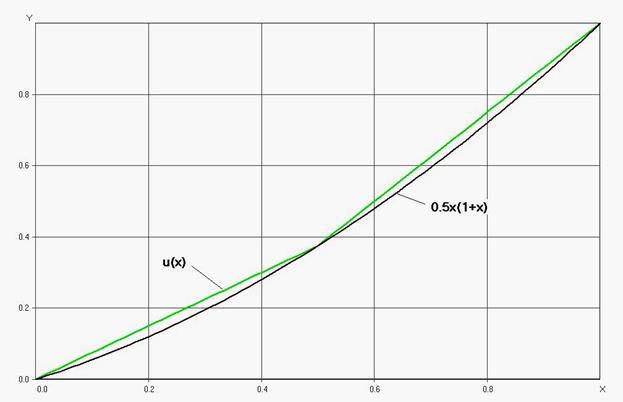
График этой функции в сравнении с точным решением 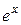показан на рисунке

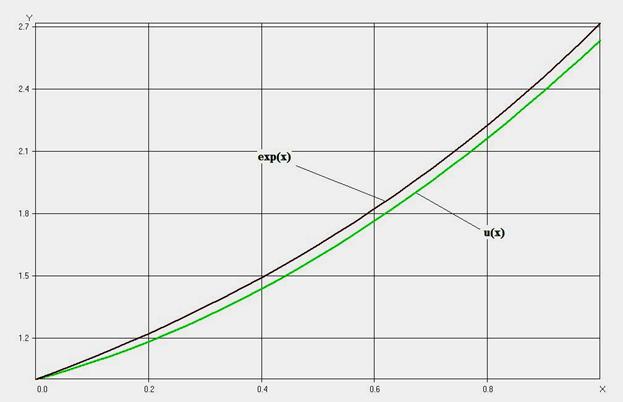
Базисные функции с кончным носителем

До сих пор мы рассматривали базисные функции, определенные всюду в 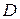. Часто такой выбор неудобен; напимер при выборе 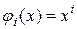при большом 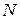получаются полиномы высокого порядка, что затрудняет вычисления. В МКЭ обычно применяют базисные функции с конечным носителем, который связан с триангуляцией области, т.е. с ее сеточным разбиением на конечные элементы. 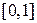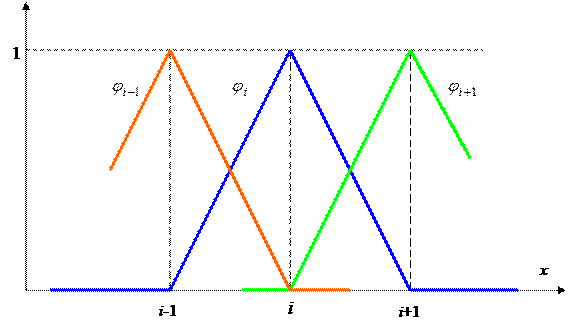Рассмотрим простейший пример равномерной сетки на отрезке с узлами 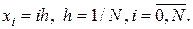Для каждого узла определим т.н. пирамидальную базисную функцию

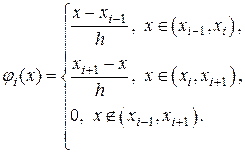(1.8)

Заметим, что

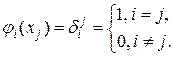(1.9)

Поэтому, во-первых, такая система базисных функций линейно-независима, а во-вторых, коэффициенты разложения (7) любой функции по этому базису будут равны значениям функции в узлах сетки, .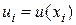

Лекция 2. Слабая (обобщенная) форма постановки краевых задач для дифференциальных уранений

Пусть 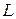‑ дифференциальный оператор, и требуется решить задачу 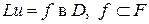. Умножим это уравнение на произвольную пробную функцию 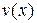и проинтегрируем по области 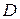. Получим

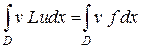(2.1)

Это уравнение должно выполняться 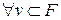. Оно называется слабой формой исходного дифференциального уравнения. Идейно слабая форма (2.1) связана с подходом Галеркина или методом взвешенных невязок, поскольку может быть представлена в виде

.

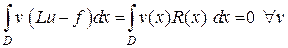Часто при записи обобщенных формулировок задач вместот интегралов используют эквивалентный символ скалярного произведения:

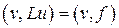(2.2)

Чтобы получить из (2.1) или (2.2) систему уравнений для узловых значений, достаточно

1) провести триангуляцию области;

2) выбрать ассоциированную с триангуляцией конечную систему базисных функций, обладающую свойством (9);

3) записать метод Галеркина ( )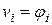

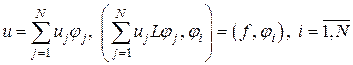(2.3)

или

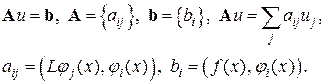(2.4)

Пример использования базисных функций с конечным носителем.

Решим задачу теплопроводности

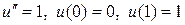. (2.5)

Точное решение задачи (2.5) 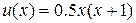. Введем сетку

;

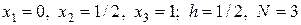выберем пирамидальные базисные функции (1.8) и подсчитаем их производные:

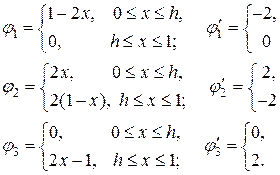(2.6)

Используя представление приближенного решения

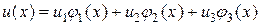(2.7)

и граничные условия в точках 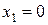и 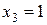, получаем

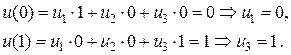
Таким образом, осталось найти коэффициент 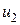. Для этого достаточно определить вторую строку системы уравнений (2.4), а именно коэффициенты 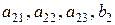. Непосредственное применение формул (2.4) для вычисления 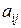невозможно, поскольку предполагает вычисления вторых производных от линейных базисных функций (2.6). Это отражает очевидный факт, что линейные функции не могут служить базисом в классе дважды дифференцируемых функций, которому принадлежит решение исходной дифференциальной задачи. Однако если ослабить требование гладкости, то с помощью формулы интегрирования по частям можно записать

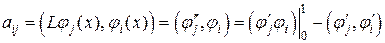(2.8)

В правую часть формулы (2.8) теперь входят лишь первые производные базисных функций, которые определены в (2.6). При этом, несмотря на то, что производные терпят разрыв в узлах сетки, можно вычислить

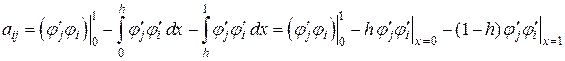(2.9)

Заметим, что для интересующих нас коэффициентов 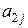подстановка в правой части (2.9) равна нулю, т.к. 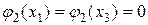. Окончательно при 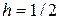получим формулу

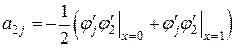(2.10)

Подставляя в (2.10) нужные значения производных из (2.6), найдем 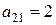, , 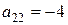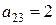. Правая часть уравнения вычисляется интегрированием

.

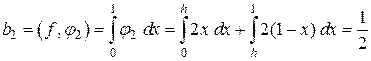Итак, второе уравнение системы уравнений для определения коэффициентов разложения имеет вид

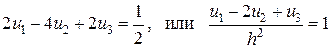. (2.11)

Нетрудно видеть, что уравнение (2.11) совпадает с конечно-разностной аппроксимацией исходного уравнения в центральном узле сетки.

Ранее с помощью граничных условий было установлено, что 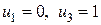, так что из (2.11) легко найти 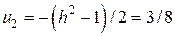. Окончательно приближенное решение задачи методом Галёркина имеет вид

.

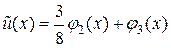На рисунке показан график этой функции в сравнении с точным решением 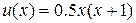.