Обобщённая форма закона дарси.

Уравнения потенциального движения

Последуем идее разложения фильтрационного потока на три составляющих течения вдоль координатных осей Ох, Оу и Оz, которая была использована при выводе уравнения неразрывности (VIII.4).

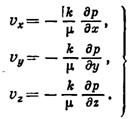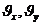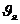В каждой точке фильтрующей среды определим значения величин составляющих вектора скорости фильтрации по координатным осям и . Для получения указанных значений возьмем формулу, выражающую закон фильтрации Дарси, и применим ее к каждому из трех составляющих потоков:

(VIII.7)

Три последние равенства равносильны одному векторному, представляющему закон Дарси в обобщенной форме:

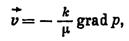(VIII.8)

где 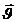— вектор скорости фильтрации;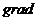 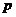— вектор — градиент давления р, имеющий в данной точке направление быстрейшего возрастания величины давления р.

Иногда записывают закон Дарси, выражая 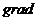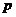через оператор Гамильтона:

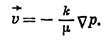(VIII.9)

Знак минус в формулах (VIII.8) и (VIII.9) показывает, что направления вектора скорости фильтрации 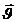и вектора — градиента давления 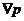противоположны.

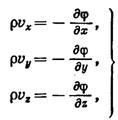Найдем проекции вектора массовой скорости фильтрации на оси координат. С этой целью умножим обе части каждого из равенств (VIII.7) на плотность 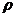. С помощью значения потенциальной функции 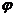получим:

(VIII.10)

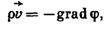где потенциальная функция 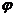определяется равенством (IV.5). Объединяя три равенства (VIII.10) в одно векторное, запишем. (VIII.11) где 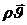— вектор массовой скорости фильтрации;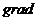 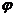- вектор - градиент потенциальной функции 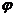, направленный в сторону быстрейшего возрастания функции .

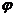Подставив значения проекции вектора массовой скорости фильтрации из (VIII.10) в уравнение (VIII.4), представим последнее в новом виде:

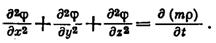(VIII.12)

При установившейся фильтрации уравнение (VIII.12) запишется так:

( VIII.13)

Левые части уравнений (VIII.12) и (VIII.13) содержат дифференциальный трехчлен, называемый лапласианом и обозначаемый символом 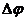или 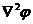; при этом уравнения (VIII.12) и (VIII.13) будут иметь соответственно такой вид:

( VIII.12а)

( VIII.13а)

Знак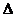и и 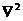символизируют оператор Лапласа. Уравнения ( VIII.12а) и ( VIII.13а)

называются уравнениями Лапласа относительно функции .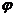

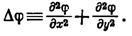Для потока, параллельного плоскости хОу, левая часть уравнения ( VIII.12) и (VIII.13) имеет такой вид:

(VIII.14)

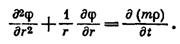Для плоско-радиального течения удобна полярная система координат. Если 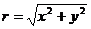, получим из (VIII.12) и (VIII.14) следующее уравнение:

(VIII.15)

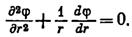Уравнение Лапласа для плоско-радиального потока в полярных координатах запишется так:

(VIII.16)

Таковы дифференциальные уравнения потенциального движения жидкости в фильтрующей среде.

З. Уравнение неразрывности в криволинейных

Координатах

При решении некоторых задач подземной гидравлики удобно связывать с неподвижной фильтрующей средой систему криволинейных координат.

Приведем без вывода уравнение неразрывности в криволинёйных координатах:

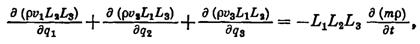(VIII.17)

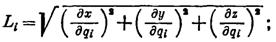где 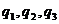— криволинейные координаты; 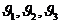— величины скоростей фильтрации вдоль касательных к соответствующим координатным линиям; 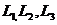— параметры Ламе, общий вид которых такой:

(VIII.18)

х, у, z - декартовы координаты точки фильтрующей среды; i - принимает значения 1, 2, 3.