Вопрос 11.1. Несобственные интегралы от неограниченных функций

Определение 11.1. Пусть функция 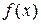определена на промежутке 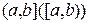, неограниченна на отрезке 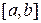и интегрируема на любом отрезке 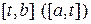, где t принадлежит 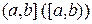. Тогда несобственным интегралом от неограниченной функции называется формальное выражение

.

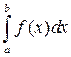Если существует предел

,

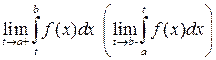то несобственный интеграл называют сходящимся. Тогда полагают:

,

.

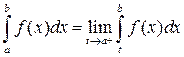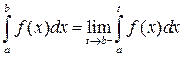Если эти пределы не существуют или бесконечны, то интегралы называются расходящимися.

Пример 11.1. .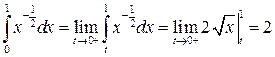

Конец примера.

Пример 11.2.

.

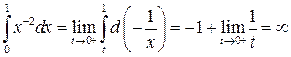интеграл расходится.

Конец примера.

Пусть 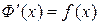, тогда введя обозначения 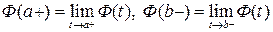, получим

,

.

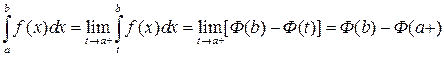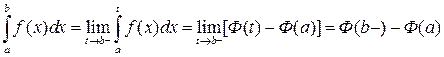Таким образом, получаем формулы типа Ньютона ‑ Лейбница

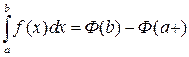, особенность при x=a.

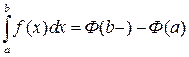, особенность при x=b.

Несобственный интеграл от неограниченной функции может быть сведен к несобственному интегралу с бесконечными пределами интегрирования. Действительно, пусть 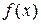неограниченна в окрестности точки a, тогда сделаем замену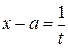

.

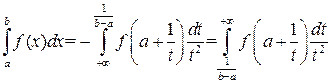Поэтому признаки сходимости могут быть построены совершенно аналогично:

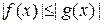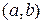Признак 11.1. Если на , то из сходимости интеграла 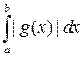следует сходимость 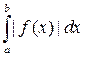, а значит и интеграла 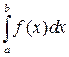, причем 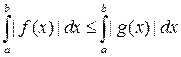. Из расходимости 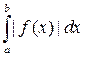следует расходимость .

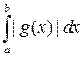Замечание 11.1. Для неотрицательных функций 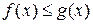из сходимости интеграла 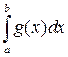следует сходимость интеграла 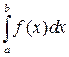, а из расходимости интеграла 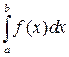следует расходимость .

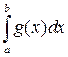Конец замечания.

Пример 11.3. 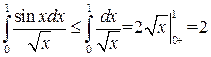. Следовательно, интеграл сходится.

Конец примера.

Признак 11.2. Есл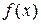и и 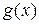неограниченны в окрестности 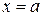, и если 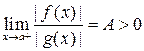, то интегралы 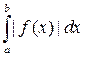и 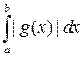сходятся или расходятся одновременно.

Пример 11.4. 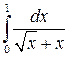, , 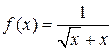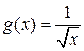и

,

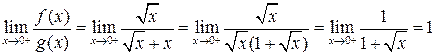но 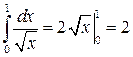, следовательно, интеграл 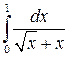сходится.

Конец примера.

Признак 11.3. Если 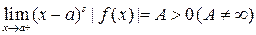, то несобственный интеграл 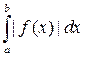сходится, если 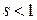и расходится, если .

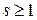Доказательство. Выберем для сравнения вторую функцию 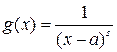. Тогда интеграл

.

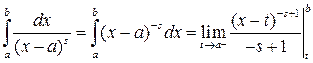сходится при 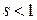и расходится при 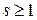. Следовательно, доказываемый признак сходимости следует из признака 11.2.

Конец доказательства.

Пример 11.5.

.

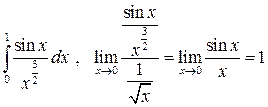Так как 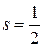, то интеграл сходится.

Конец примера.

Вопрос 11.2. Несобственные интегралы от функции, имеющие несколько особенностей.

Пусть функция 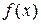определена на 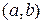и интегрируема на любом отрезке 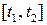из интервала 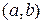, тогда

.

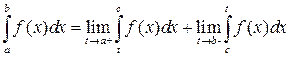Интеграл называется сходящимся, если оба предела конечны и расходящимся в противном случае. Аналогично, как в вопросе 11.1, можно вывести формулу типа Ньютона-Лейбница.

.

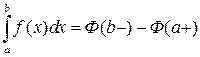Пример 11.6.

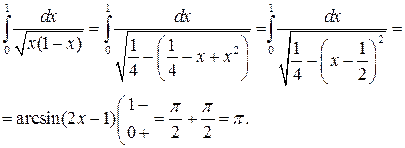
Конец примера.

Пусть функция 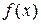имеет особенности в точках 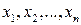из интервала 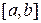. Тогда положим по определению

.

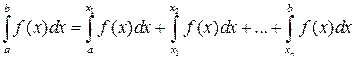Если все интегралы сходятся, то несобственный интеграл 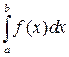называется сходящимся, в противном случае интеграл называется расходящимся.

Пример 11.7.

.

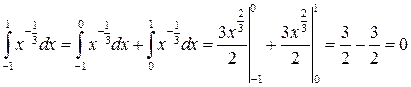Конец примера.