Неполные дифференциальные уравнения (первого порядка).Уравнения Лагранжа и Клеро
Дифференциальное уравнение первого порядка 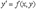 называются неполными, если в нем не содержится (явно) или сама функция у, или независимая переменная х.
называются неполными, если в нем не содержится (явно) или сама функция у, или независимая переменная х.
В том случае, когда правая часть дифференциального уравнения не содержит самой функции у, оно принимает вид:
 или
или  , или
, или 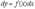 .
.
Отсюда 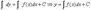 .
.
Таким образом, получено общее решение неполного дифференциального уравнения. Фактически это задача об отыскании первообразной функции (т.е. это непосредственно задача неопределенного интеграла).
Во втором случае, т.е. когда дифференциальное уравнение имеет вид 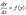 , т.е. в уравнение явно не входит независимая переменная х.
, т.е. в уравнение явно не входит независимая переменная х.
Дифференциальное уравнение принимает вид 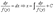 , т.е. получаем у – как независимую переменную, а х – как функцию от у (фактически это обратная функция по отношению к функции у от х).
, т.е. получаем у – как независимую переменную, а х – как функцию от у (фактически это обратная функция по отношению к функции у от х).
| Уравнения Лагранжа и Клеро |
Уравнение Лагранжа Дифференциальное уравнение вида 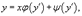 где φ(y') и ψ(y') − известные функции, дифференцируемые на некотором интервале, называется уравнением Лагранжа. Полагая y' = p и дифференцируя по переменной x, получаем общее решение уравнения в параметрической форме: где φ(y') и ψ(y') − известные функции, дифференцируемые на некотором интервале, называется уравнением Лагранжа. Полагая y' = p и дифференцируя по переменной x, получаем общее решение уравнения в параметрической форме: 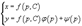 при условии, что при условии, что 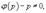 где p − параметр. Уравнение Лагранжа может также иметь особое решение, если нарушается условие φ(p) − p ≠ 0. Особое решение определяется функцией где p − параметр. Уравнение Лагранжа может также иметь особое решение, если нарушается условие φ(p) − p ≠ 0. Особое решение определяется функцией 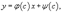 где c − корень уравнения φ(p) − p = 0. Уравнение Клеро Уравнение Клеро имеет вид: где c − корень уравнения φ(p) − p = 0. Уравнение Клеро Уравнение Клеро имеет вид: 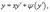 где ψ(y') − некоторая нелинейная дифференцируемая функция. Уравнение Клеро является частным случаем уравнения Лагранжа, когда φ(y') = y'. Оно решается аналогичным образом с помощью введения параметра. Общее решение определяется выражением где ψ(y') − некоторая нелинейная дифференцируемая функция. Уравнение Клеро является частным случаем уравнения Лагранжа, когда φ(y') = y'. Оно решается аналогичным образом с помощью введения параметра. Общее решение определяется выражением 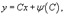 в котором C − произвольная постоянная. Также как и уравнение Лагранжа, уравнение Клеро может иметь особое решение, которое выражает в параметрической форме: в котором C − произвольная постоянная. Также как и уравнение Лагранжа, уравнение Клеро может иметь особое решение, которое выражает в параметрической форме: 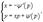 где p − параметр. где p − параметр. |
| Пример 1 |
Найти все решения дифференциального уравнения y = 2xy' − 3(y')2. Решение. Здесь мы имеем дело с уравнением Лагранжа. Буде м решать его методом введения параметра. Обозначим y' = p, так что уравнение можно записа ть в форме: 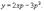 Дифференцируя обе части, получаем: Дифференцируя обе части, получаем: 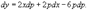 Дифференциал dy можно заменить на pdx: Дифференциал dy можно заменить на pdx: 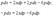 Разделив на p, можно записать следующее уравнение (позже мы проверим, не является ли p = 0 решением исходного уравнения): Разделив на p, можно записать следующее уравнение (позже мы проверим, не является ли p = 0 решением исходного уравнения):  Как видно, мы получили линейное уравнение для функции x(p). Интегрирующий множитель будет равен: Как видно, мы получили линейное уравнение для функции x(p). Интегрирующий множитель будет равен: 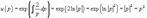 Тогда общее решение линейного дифференциальног о уравнения имеет вид: Тогда общее решение линейного дифференциальног о уравнения имеет вид: 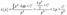 Подставляя это выражение для x в уравнение Лагранжа, находим: Подставляя это выражение для x в уравнение Лагранжа, находим: 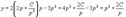 Таким образом, общее решение в параметрической форме определяется системой уравнений: Таким образом, общее решение в параметрической форме определяется системой уравнений: 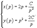 Кроме общего решения, уравнение Лагранжа може т иметь еще особое решение. Решая алгебраическо уравнение φ(p) − p = 0, находим корень: Кроме общего решения, уравнение Лагранжа може т иметь еще особое решение. Решая алгебраическо уравнение φ(p) − p = 0, находим корень: 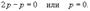 Следовательно, особое решение представляется в в иде следующей линейной функции: Следовательно, особое решение представляется в в иде следующей линейной функции: 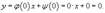 Найти общее и особое решения дифференциального уравнения y = xy' + (y')2. Решение. Здесь мы имеем дело с уравнением Клеро. Полагая y' = p, его можно записать в виде Найти общее и особое решения дифференциального уравнения y = xy' + (y')2. Решение. Здесь мы имеем дело с уравнением Клеро. Полагая y' = p, его можно записать в виде 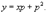 Продифференцировав по переменной x, находим: Продифференцировав по переменной x, находим: 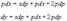 Заменим dy на pdx: Заменим dy на pdx: 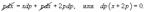 Приравнивая первый множитель к нулю, получаем: Приравнивая первый множитель к нулю, получаем:  Теперь подставим это во второе уравнение: Теперь подставим это во второе уравнение: 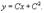 В результате получаем общее решение заданного уравнения Клеро. Графически, это решение представляется в виде однопараметрического семейства прямых. Приравнивая нулю второй сомножитель, находим еще одно решение: В результате получаем общее решение заданного уравнения Клеро. Графически, это решение представляется в виде однопараметрического семейства прямых. Приравнивая нулю второй сомножитель, находим еще одно решение: 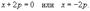 Это уравнение соответствует особому решению дифференциального уравнения и в параметрической форме записывается как Это уравнение соответствует особому решению дифференциального уравнения и в параметрической форме записывается как 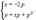 Исключая p из системы, получаем следующее уравнение интегральной кривой: Исключая p из системы, получаем следующее уравнение интегральной кривой: 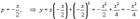 |
