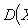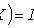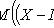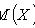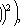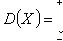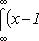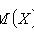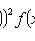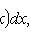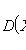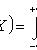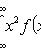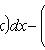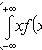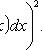Непрерывные случайные величины. Интегральная функция распределения. Плотность распределения вероятностей

Математическое ожидание и дисперсия для биномиального закона.

МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ

среднее значение, случайной величины - числовая характеристика распределения вероятностей случайной величины. Самым общим образом М. о. случайной величины Х(w), определяется как интеграл Лебега по отношению к вероятностной мере в исходном вероятностном пространстве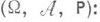

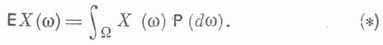
М. о. может быть вычислено и как интеграл Лебега от хпо распределению вероятностей Р _Х величины X:

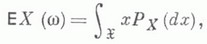
где 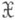- множество всех возможных значений X. М. о. функций от случайной величины Xвыражается через распределение Р _Х:напр., если X - случайная величина со значениями в 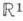и f(x) - однозначная бо-релевская функция х, то

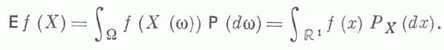
Если F(x) - функция распределения X, то М. о. представимо интегралом Лебега - Стилтьеса (или Римана - Стилтьеса)

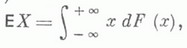
при этом интегрируемость Xв смысле (*) равносильна конечности интеграла

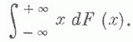
В частных случаях, если Xимеет дискретное распределение с возможными значениями х _k, k=1, 2, . . ., и соответствующими вероятностями 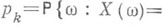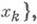то

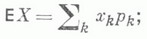
если Xимеет абсолютно непрерывное распределение с плотностью вероятности р(х), то

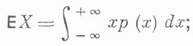
при этом существование М. о. равносильно абсолютной сходимости соответствующего ряда или интеграла. Основные свойства М. о.:

а)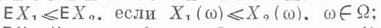

б) ЕС=С для любого действительного С:

в)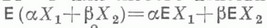

для любых действительных a и b;

г)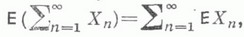

если сходится ряд

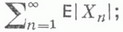
д) 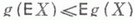для выпуклых функции g(x).

е) любая ограниченная случайная величина имеет конечное М. о. Кроме того,

ж)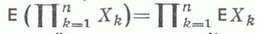

для взаимно независимых случайных величин X₁, ..., Х _п.

Биномиальное распределение

Биноминальный закон распределения

Биноминальное распределение - это распределение вероятностей возможных чисел появления события А при n независимых испытаниях, в каждом из которых событие А может осуществиться с одной и той же вероятностью Р(А) = р = const. Кроме события А может произойти также противоположное событие Ā, вероятность которого Р(Ā) = 1 - р = q.

Вероятности любого числа событий соответствуют членам разложения бинома Ньютона в степени, равной числу испытаний:

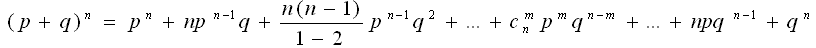
где p^{n -} вероятность того, что при n испытаниях событие А наступит n раз;

qⁿ - вероятность того, что при n испытаниях событие А не наступит ни разу;

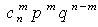- вероятность того, что при n испытаниях событие А наступит m раз, а событие Āнаступит n-m раз;

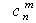- число сочетаний (комбинаций) появления события А и Ā.

Числовые характеристики биноминального распределения:

М(m)=np - математическое ожидание частоты появления события А при n независимых испытаниях;

D(m)=npq - дисперсия частоты появления события. А;

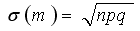- среднее квадратическое отклонение частоты.

Непрерывные случайные величины. Интегральная функция распределения. Плотность распределения вероятностей

Функцией распределения вероятностей называют функцию 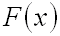, определяющую вероятность того, что случайная величина 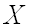в результате испытания примет значение, меньшее 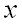, то есть:
.
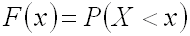Случайную величину называют непрерывной, если ее функция распределения вероятностей есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.

Интегральная функция (функция распределения)

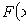
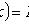
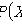
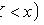
Свойства:

1) ;

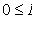
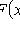
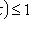2) ;

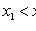
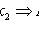
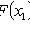
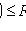
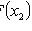3) ;

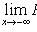
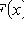
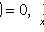
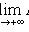
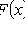
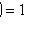4) .

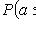
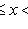
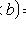
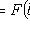
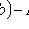
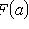Дифференциальная функция распределения (плотность вероятности)

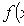
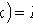
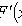
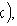
где F(x) - интегральная функция.

Свойства:

1) ;

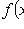
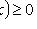2) ;

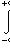
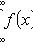
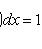3) ;

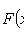
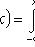
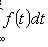4) .

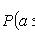
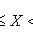
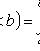
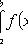
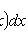Числовые характеристики непрерывной случайной величины

Математическое ожидание

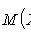
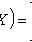
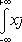
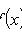
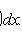
Дисперсия