Криволинейный интеграл второго рода

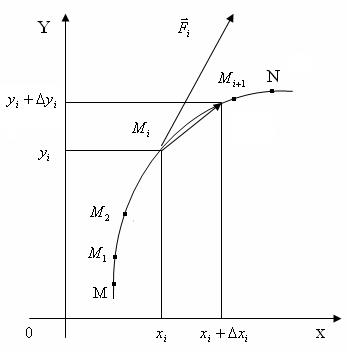
Пусть т. Р(x,y) движется вдоль некоторой плоской линии L от точки М к точке N. К точке Р приложена сила 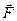, которая меняется по величине и направлению при перемещении т. Р вдоль кривой L, т.е. 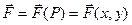представляет

собой функцию координат точки Р.

Вычислим работу А силы 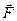при перемещении т. Р из положения М в положение N. Для этого разобьем кривую MN на n частей точками

М₀ = М, М₁, М₂, …, М_n = N

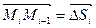Обозначим вектор , величину силы 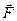в т.М_i через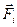

Тогда 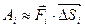- работа силы 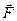вдоль дуги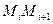

Пусть ,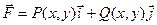

где P(x, y), Q(x, y) – проекции вектора 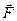на оси ox, oy,

а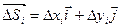

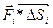– скалярное произведение двух векторов.

Следовательно

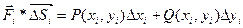
Работа А силы 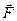на всей кривой MN будет

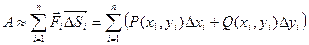
Существует предел правой части при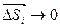

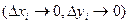
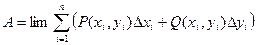
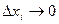
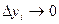
Этот предел называют криволинейным интегралом второго рода и обозначают

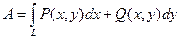или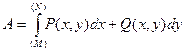

(М) – читаем т. М, (N) – точка N.

Если кривая L пространственная, то

)
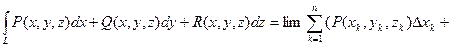
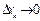
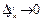
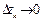
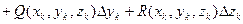