Сумма абсолютных отклонений значений признака от медианы, меньше, чем от другой любой величины

При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:

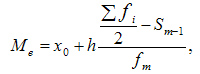,где: x₀— нижняя граница интервала, который содержит медиану, h— величина интервала, 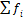— сумма частот или число членов ряда, S_m-1- сумма накопленных частот интервалов, предшествующих медианному, f_m— частота медианного интервала.

Относительные показатели вариации включают:

• Коэффициент осцилляции
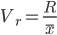
• Относительное линейное отклонение (линейный коэффициент варианции)
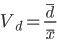
• Коэффициент вариации (относительное отклонение)

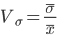
Сравнение вариации нескольких совокупностей по одному и тому же признаку, а тем более по различным признакам с помощью абсолютных показателей не представляется возможным. В этих случаях для сравнительной оценки степени различия строят относительные показатели вариации. Они вычисляются как отношения абсолютных показателей вариации к средней.

Вопрос

Индексный метод расчета

Индексы являются относительными величинами, характеризующими изменение уровней простых или сложных социально-экономических явлений во времени, пространстве или по сравнению с планом, то есть это соответственно относительные показатели динамики (индексы динамики), относительные показатели сравнения (территориальные индексы) и относительные показатели плана и выполнения плана.

От обычных относительных показателей индексы отличаются тем, что характеризуют изменение не только простых, но и сложных явлений. Сложные явления состоят из непосредственно несоизмеримых элементов, а простые – только из однородных элементов.

Показатель, для которого рассчитывается индекс, называется индексируемой величиной. Так, в индексе себестоимости индексируемой величиной является себестоимость, в индексе физического объема – объем выпуска в натуральном выражении.

С помощью индексов решаются следующие задачи:

1. Оценка изменений сложных явлений и отдельных их частей (например, на сколько в текущем периоде изменился объем продаж по сравнению с предыдущим).

2. Определение влияния отдельных факторов на общую динамику сложного явления (например, влияние изменения цен на объем продаж), для чего используется индексный анализ.

В практической деятельности используются разнообразные индексы, которые можно классифицировать по следующим основаниям:

• содержание изучаемых объектов (характер);

• степень охвата элементов совокупности;

• методы расчета.

По содержанию и характеру изучаемых показателей различают

два вида индексов:

- индексы количественных показателей (объемных) К ним относятся индексы физического объема произведенной продукции, физического объема потребления и т.д. Индексируемой величиной в таких индексах является объемный показатель, измеряемый в натуральных единицах.

- индексы качественных показателей Эти индексы используются для измерения изменения показателя, рассчитываемого на единицу совокупности. Такие показатели называются качественными и характеризуют интенсивность изучаемого явления или процесса. Индексируемой величиной в индексах качественных показателей является уровень явления в расчете на единицу совокупности. К индексам качественных показателей относятся индекс цен, себестоимости единицы продукции, трудоемкости, производительности труда и т.д.

По степени охвата элементов совокупности выделяют три формы индексов:

- индивидуальные,

- сводные (общие),

- групповые (субъиндексы).

Индивидуальные индексы характеризуют изменение отдельных элементов, входящих в состав сложного явления. Это простая форма индексов (например, индивидуальный индекс цен отдельного вида товара).

Сводные индексы характеризуют изменение всего сложного явления, выражаемого сложным показателем. В таком явлении его элементы являются величинами несопоставимыми. Для решения проблемы несопоставимости индексируемых величин используются специальные показатели, называемые соизмерителями индексируемых величин (статическими весами).

Групповые индексы (субъиндексы) рассчитываются для определенной части элементов совокупности. Например, индекс физического объема по отдельным отраслям или территориям.

По методам расчета классифицируются только общие индексы. Они делятся на агрегатные и средние.

В агрегатных индексах числитель и знаменатель (величина и база сравнения) представляют собой набор или агрегат разнородных элементов («aggregatus» - складываемый, суммируемый).

Средние индексы используются в тех случаях, когда данных для построения агрегатных индексов недостаточно. Они рассчитываются на основе индивидуальных индексов и делятся на средние арифметические и средние гармонические индексы.

51вопрос
Аналитические показатели рядов динамики: назначение и методика расчета

Ряд динамики (временной ряд) – совокупность (последовательность) количественных значений какого-либо признака за определенный период времени или в определенные моменты времени. Может быть моментным (конкретная дата) и интервальным (промежуток времени – год).

Базисные показатели – значения текущего периода сравниваются со значением периода, имеющим первое место во временном ряду (базисом).

Цепные показатели – значение показателя сравнивают со значением показателя, предшествующего периода.

Абсолютный прирост Δ характеризует размер увеличения (уменьшения) уровня ряда по сравнению с выбранной базой:

• цепной абсолютный прирост показывает, на сколько изменилось значение данного уровня по сравнению с предыдущим, то есть приращение уровня по сравнению с предыдущим: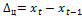

• базисный абсолютный прирост показывает, на сколько изменилось значение данного уровня по сравнению с исходным (начальным) уровне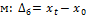

Коэффициент роста характеризует интенсивность изменения уровней ряда (скорость изменения уровней). Он показывает, во сколько раз уровень данного периода выше или ниже базисного уровня. Этот показатель как относительная величина, выраженная в долях единицы, называется коэффициентом (индексом) роста; выраженная в процентах, называется темпом роста.

• Цепной коэффициент роста показывает, во сколько раз текущий уровень выше или ниже предыдущего: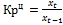

• Базисный коэффициент роста показывает, во сколько раз текущий уровень выше или ниже начального уровня: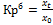

Темп роста: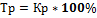

Темп прироста: 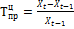; Т^б_пр=*** ; Т_пр=К_пр*100%; Т_пр=Т_р-100.

Средние показатели ряда динамики.

Средний уровень ряда – простая арифметическая средняя.

Для моментного ряда: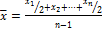

Среднее абсолютное изменение уровней ряда: = ;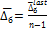

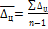Среднее относительное изменение: ;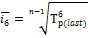

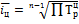
52 вопрос
Расчет относительных величин. База в относительных величинах. Виды относительных величин.
Относительная величина – показатель, который является мерой соотношения двух сопоставляемых статистических характеристик. Величина, с которой производится сравнение, называется базисной (базой сравнения), а та, с которой сравнивают, - текущей (отчетной).

Относительные показатели выражаются в разных формах - коэффициентов, процентов, промилле, продецимилле. Если база сравнения принимается за единицу, то относительный показатель выражается в форме коэффициента.

С помощью относительных величин на основе различного рода сравнений обеспечивается оценка изучаемых свойств явлений, проводится анализ их значения и результатов развития. Сравнение проводят во времени, пространстве или с плановыми данными; может быть сравнение части и целого, отдельных частей целого между собой. В связи с этим различают:

Относительная величина динамики – отношение данного (отчетного) уровня изучаемого явления к уровню за предшествующий период: 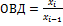. ОВД рассчитывается так же с постоянной базой сравнения х₀.

Относительная величина сравнения – отношение одноименных показателей, характеризующие различные объекты или территории: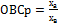

Относительная величина планового задания – отношение предусмотренного планом уровня или объема к соответствующему фактически достигнутому уровню за предшествующий период: 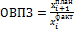. Показывает, во сколько раз планируется произвести больше/меньше, чем на сегодня.

Относительная величина выполнения плана отражает степень реализации выполнения плановых заданий и вычисляется как отношение фактически достигнутого уровня к плановому заданию: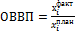

Относительная величина структуры – отношение части к целому; показывает, какой удельный вес (долю) составляет каждая часть совокупности в общей ее численности или общем объеме изучаемого признака: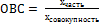

Относительная величина координации – отношение отдельных частей целого к одной из них, взятой за базу сравнения. Такие показатели позволяют анализировать пропорции между отдельными элементами совокупности, например, соотношение в общем числе образовательных учреждений государственных и негосударственных.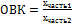

Относительная величина интенсивности – характеризует степень распространения данного явления в определенной среде: 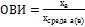. Например для измерения интенсивности процессов рождаемости, смертности соответствующие абсолютные величины соотносят к средней численности населения.

53 вопрос
Расчет показателя ВВП тремя способами: производственным, по доходам, по конечному использованию

Производственный: ВВ-ПП+(Н-С)

Метод конечно использования: КП+ВН+Э-И

По источникам доходов: ОТ+(ЧНИ)+СД+П

ВВ-валовой выпуск продукции, ПП-промежуточное потребление, (Н-С)-налоги за вычетом субсидий на продукты, КП-конечное потребление, ВН-валовое накопление, Э-экспорт, И-импорт, ОТ-оплата труда работников, ЧНИ-налоги за вычетом субсидий на производство и импорт, СД-смешанные доходы, П-прибыль.

Применимы так же расчет на основе валовой добавленной стоимости (ВНД). Если продукция выражена в основных ценах: 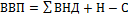, если в ценах производителя: 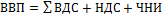; ЧНИ-читые налоги на импорт.

Вопрос

Ряды динамики: понятие, структура и классификация

Ряд динамики-последовательность(совокупность) качественных значений признака в определенный момент времени или за определенный период времени

абсолютный прирост
∆y=Xt-Xt-1( цепной показатель)

∆б=Хt-Xб

Темп(коэффициент) роста

Тр(базисный)= Хt÷X0×100%

Кр=Тр÷100%

Тр(у)= Xt÷Xt-1×100%