Дифференциальные уравнения движения материальной точки

С помощью дифференциальных уравнений движения решается вторая задача динамики. Правила составления таких уравнений зависят от того, каким способом хотим определить движение точки.

1) Определение движения точки координатным способом.

Пусть точка М движется под действием нескольких сил (рис. 13.2). Составим основное уравнение динамики 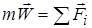и спроектируем это векторное равенство на оси x, y, z:

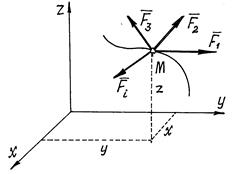
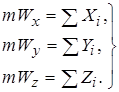
Но проекции ускорения на оси есть вторые производные от координат точки по времени. Поэтому получим

Рис. 13.2.

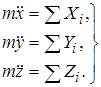(13.1)

Эти уравнения и являются дифференциальными уравнениями движения материальной точки. Решив их, с учётом начальных условий, получим уравнения движения точки: x = x(t), y = y(t), z = z(t).

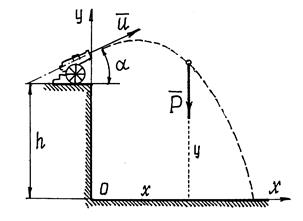Пример 13.2. Из пушки, установленной на высоте h, произвели выстрел под углом a к горизонту (рис. 13.3.). Ядро вылетело из ствола орудия со скоростью u. Определим уравнения движения ядра.

Чтобы правильно составить дифференциальные уравнения движения, надо решать подобные задачи по определённой схеме.

Рис. 13.3.

а) Назначить систему координат (количество осей, их направление и начало координат). Удачно выбранные оси упрощают решение.

б) Показать точку в промежуточном положении. При этом надо проследить за тем, чтобы координаты такого положения обязательно были положительными (рис. 13.3.).

в) Показать силы действующие на точку в этом промежуточном положении (силы инерции не показывать!).

В примере 13.2 – это только сила 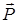, вес ядра. Сопротивление воздуха учитывать не будем.

г) Составить дифференциальные уравнения по формулам (13.1): 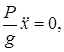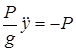. Отсюда получим два уравнения: 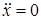и .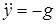

д) Решить дифференциальные уравнения.

Полученные здесь уравнения – линейные уравнения второго порядка, в правой части – постоянные. Решение этих уравнений элементарно.

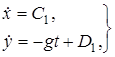и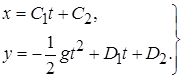

Осталось найти постоянные интегрирования. Подставляем начальные условия (при t = 0 x = 0, y = h, 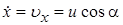, 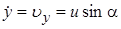) в эти четыре уравнения: u cosa = C₁, u sina = D₁, 0 = С₂, h = D₂.

Подставляем в уравнения значения постоянных и записываем уравнения движения точки в окончательном виде

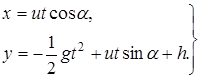
Имея эти уравнения, как известно из раздела кинематики, можно определить и траекторию движения ядра, и скорость, и ускорение, и положение ядра в любой момент времени.

Как видно из этого примера, схема решения задач довольно проста. Сложности могут возникнуть только при решении дифференциальных уравнений, которые могут оказаться непростыми.

2) Определение движения точки естественным способом.

Координатным способом обычно определяют движение точки, не ограниченные какими-либо условиями, связями. Если на движение точки наложены ограничения, на скорость или координаты, то определить такое движение координатным способом совсем не просто. Удобнее использовать естественный способ задания движения.

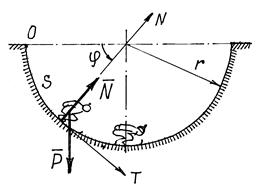
Определим, например, движение точки по заданной неподвижной линии, по заданной траектории (рис. 13.4.).

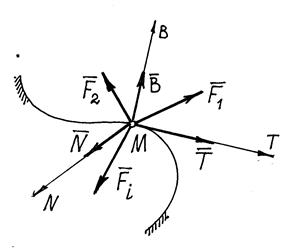На точку М кроме заданных активных сил 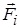, действует реакция линии. Показываем составляющие реакции 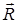по естественным осям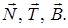

Составим основное уравнение динамики 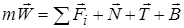и спроектируем его на естественные оси

Рис. 13.4.

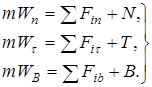
Так как 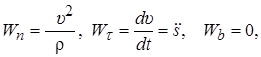то получим дифференциальные уравнения движения, такие

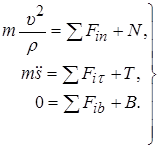(13.2)

Здесь сила 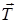- сила трения. Если линия, по которой движется точка, гладкая, то Т=0 и тогда второе уравнение будет содержать только одну неизвестную – координату s:

.

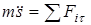Решив это уравнение, получим закон движения точки s=s(t), а значит, при необходимости, и скорость и ускорение. Первое и третье уравнения (13.2) позволят найти реакции 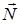и .

Рис. 13.5.

Пример 13.3. Лыжник спускается по цилиндрической поверхности радиуса r. Определим его движение, пренебрегая сопротивлениями движению (рис. 13.5).

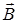Схема решения задачи та же, что и при координатном способе (пример 13.2). Отличие лишь в выборе осей . Здесь оси N и Т движутся вместе с лыжником. Так как траектория – плоская линия, то ось В, направленную по бинормали, показывать не нужно (проекции на ось В действующих на лыжника сил будут равны нулю).

Дифференциальные уравнения по (13.2) получим такие

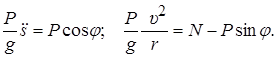(13.3)

Первое уравнение получилось нелинейным: 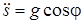. Так как s=rj, то его можно переписать так: 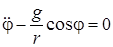. Такое уравнение можно один раз проинтегрировать. Запишем 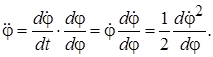Тогда в дифференциальном уравнении переменные разделятся: 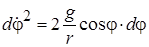. Интегрирование дает решение 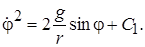Так как при t=0 j=0 и 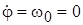, то С₁=0 и 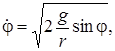а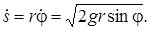

К сожалению, в элементарных функциях второй интеграл найти невозможно. Но и полученное решение позволяет сделать некоторые выводы. Можно найти скорость лыжника в любом положении как функцию угла j. Так в нижнем положении, при 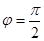, 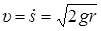. А из второго уравнения (13.3) при 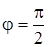можно определить давление: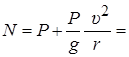 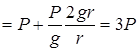. То есть давление на лыжника в нижнем положении равно его трехкратному весу.