Изучение затухающих колебаний и определение коэффициента затухания
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ИЖЕВСКАЯ ГОСУДАРСТВЕННАЯ СЕЛЬСКОХОЗЯЙСТВЕННАЯ
АКАДЕМИЯ»
Кафедра физики
Лаборатория механики и молекулярной физики №2(411)
ЛАБОРАТОРНАЯ РАБОТА №8
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ И ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ЗАТУХАНИЯ
Отредактировал: доцент кафедры физики
Новожилова С.Р.
Ижевск 2013
ЛАБОРАТОРНАЯ РАБОТА №8
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ И ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ЗАТУХАНИЯ
Цель работы: ознакомление с характером собственных колебаний и вычисление коэффициента затухания.
Приборы и принадлежности: 1) маятник со шкалой отсчёта, 2) электросекундомер.
Колебательным называется движение, при котором материальная точка или тело многократно отклоняясь от своего положения равновесия, вновь возвращается к нему. Время одного полного колебания называется периодом. Наибольшее отклонение маятника от положения равновесия называется амплитудой колебания.
На практике всякое колебание, если оно не поддерживается извне, затухает: амплитуда колебаний с течением времени уменьшается, так как на движущееся тело действует сила трения окружающей среды.
Результирующая сила F, действующая на тело, равна сумме квазиупругой силы 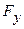 и силы трения
и силы трения 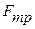 . При малых скоростях движения сила трения пропорциональна скорости и направлена в противоположную сторону, т. е.
. При малых скоростях движения сила трения пропорциональна скорости и направлена в противоположную сторону, т. е. 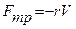 , где r- коэффициент трения, зависящий от свойств среды, формы и размеров движущегося тела.
, где r- коэффициент трения, зависящий от свойств среды, формы и размеров движущегося тела.
По второму закону Ньютона F = ma, или 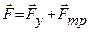 (1)
(1)
Если учесть, что 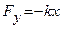 ,
, 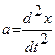 и
и 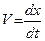 , то формула (1) примет вид
, то формула (1) примет вид 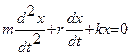 (2)
(2)
или 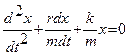 (3)
(3)
Это и есть дифференциальное уравнение затухающих колебаний. Оно имеет два решения 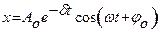 или
или 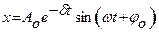 , где
, где 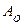 и
и 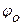 - соответственно начальные амплитуды и фаза, х – смещение в данный момент времени,
- соответственно начальные амплитуды и фаза, х – смещение в данный момент времени, 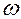 – циклическая частота, равная
– циклическая частота, равная 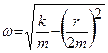 ,
, 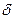 – коэффициент затухания, равный
– коэффициент затухания, равный 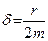 , e – основание натуральных логарифмов. Величина
, e – основание натуральных логарифмов. Величина 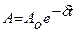 – амплитуда колебаний, убывает с течением времени. Быстроту уменьшения ее характеризует коэффициент
– амплитуда колебаний, убывает с течением времени. Быстроту уменьшения ее характеризует коэффициент 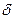 , он обратен по величине тому промежутку времени, за который амплитуда уменьшается в e раз.
, он обратен по величине тому промежутку времени, за который амплитуда уменьшается в e раз.
В данной работе нужно определить коэффициент затухания колебаний для маятника.
Чтобы получить более удобное выражение для определения 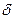 , возьмем отношение двух амплитуд, разделённых отрезком времени в один период
, возьмем отношение двух амплитуд, разделённых отрезком времени в один период 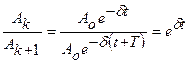 , т. е. амплитуда за каждый период убывает в одно и то же число раз.
, т. е. амплитуда за каждый период убывает в одно и то же число раз.
Натуральный логарифм этого отношения
|

 ln
ln 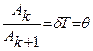 (4)
(4) носит название логарифмического декремента затухания.
Таким образом, чтобы определить коэффициент затухания 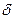 , нужно определить логарифмический декремент θ и период Т.
, нужно определить логарифмический декремент θ и период Т.
|

|

|
|
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Задание 1. ОПРЕДЕЛЕНИЕ ЛОГАРИФМИЧЕСКОГО ДЕКРЕМЕНТА ЗАТУХАНИЯ
1. Определить по миллиметровой линейке положение равновесия маятника.
2. Отклонив маятник от положения равновесия вправо на некоторый угол (не более 5-60), измерить начальную амплитуду.
3. Измерить не менее 5 амплитуд вправо, разделённых промежутком времени в один период.
4. Отклонив маятник на тот же угол и в ту же сторону, как в первом случае, измерить 5 левых амплитуд. Все данные занести в таблицу 1.
5. По измеренным данным найти отношение амплитуд 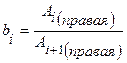 и
и 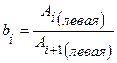 , разделённых интервалом в один период, и занести их в таблицу 1.
, разделённых интервалом в один период, и занести их в таблицу 1.
6. По стандартной методике, приведённой в приложении, найти абсолютную и относительную погрешности для b. Коэффициент надёжности 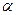 задаёт преподаватель. Результаты занести в таблицу 1.
задаёт преподаватель. Результаты занести в таблицу 1.
7. Вычислить логарифмический декремент затухания по формуле: 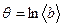 ,
,
а также его погрешности: 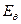 = Еb,
= Еb, 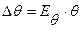 . Результаты занести в таблицу 2.
. Результаты занести в таблицу 2.
8. Округлив полученные результаты, записать ответ по форме:
Ответ: логарифмический декремент затухания равен:
θ = (<θ>± Dθ)
Результаты занести в таблицу 2.
Пример. Ответ: момент инерции диска равен:
I = (0,10 ± 0,01) кг×м2. 
Таблица 1 Измерение амплитуд свободных колебаний
| № изм. | Амплитуды | bi | Δbi | (Δbi)2 | Данные и результат | |
| Правые | ||||||
| <b>= | ||||||
| n(n-1)= | ||||||
Snb= 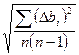 = = | ||||||
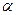 = = | ||||||
| tnα = | ||||||
| Левые | Δbp= Snb. tnα = | |||||
| Δb = | ||||||
Еb = 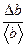 = = | ||||||
| ΔA = | ||||||
b= <b> 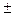 Δb = Δb = | ||||||
Таблица 2 Определение логарифмического декремента
| Логарифмический декремент θ | 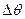 | 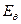 | θ = (<θ>± Dθ) ед. измерения |
Задание 2. ОПРЕДЕЛЕНИЕ ПЕРИОДА КОЛЕБАНИЙ И ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТА ЗАТУХАНИЯ
1. Привести маятник в колебательное движение. По секундомеру определить время t, в течение которого происходит n = 10 полных колебаний. Опыт повторить не менее 5-ти раз. Все измерения занести в таблицу 3.
2. По стандартной методике, приведённой в приложении, найти абсолютную и относительную погрешности времени t. Коэффициент надёжности α задаёт преподаватель. Результаты занести в таблицу 3.
Таблица 3 Определение периода колебаний
| № изм. | ti, c | Δti, c | (Δti)2, c2 | Данные и результат |
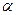 = = | ||||
| tnα = | ||||
| σ = | ||||
| Δt = | ||||
Еt = 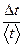 = = | ||||
| n(n-1)= | <t>= | Δtp= | Snt= | t = <t> 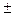 Δt = Δt = |
3. Из полученных данных определить период колебаний маятника по формуле: 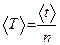 . Результаты занести в таблицу 4.
. Результаты занести в таблицу 4.
4. Вычислить коэффициент затухания колебаний по формуле: 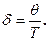
5. Найти относительную и абсолютную погрешности коэффициента затухания по формулам: Δδ = δ.Еδ, Еδ = Еθ. Результаты занести в таблицу 4.
Таблица 4 Вычисление коэффициента затухания
| Логарифмический декремент θ | Период колебаний <Т>, с | Коэффициент затухания δ, с-1 | Δδ, с -1 | Еδ | δ = (<δ>± Dδ) ед. измерения |
6. Округлив полученные результаты, записать ответ по форме:
Ответ: коэффициент затухания равен:
δ = (<δ>± Dδ) ед. измерения.
Результаты занести в таблицу 4.
Пример. Ответ: момент инерции кольца равен:
I = (0,204 ± 0,001) кг×м2. 
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какое движение называется колебательным?
2. Вывести уравнение затухающих колебаний.
3. Что называется коэффициентом затухания, от чего он зависит?
4. Что называется логарифмическим декрементом затухания?
5. Как связаны θ и δ?
6. Какое колебание называется затухающим?
ЛИТЕРАТУРА
1. Савельев И.В. Курс общей физики. 1982, т.1, § 58.
2. Зисман Г.А., Тодес О.М. Курс общей физики. 1972, т,1, § 54.
3. Грабовский Р.И. Курс физики. 1980, ч.1, § 31.
Приложение
