Уравнение затухающих колебаний и его решение. Коэффициент затухания. Логарифмический декремент затухания. Добротность.
Затухающие колебания — колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются.
Закон затухания колебаний определяется свойствами колебательных систем. Обычно рассматривают линейные системы — идеализированные реальные системы, в которых параметры, определяющие физические свойства системы, в ходе процесса не изменяется. Различные по своей природе линейные системы описываются идентичными линейными дифференциальными уравнениями.
Дифференциальное уравнение свободных затухающих колебаний линейной системы
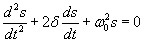
где s — колеблющаяся величина, описывающая тот или иной физический процесс, δ = const — коэффициент затухания, (ω0 — циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при δ =0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы. Решение уравнения рассмотрим в виде
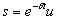(7.1) где u=u(t).
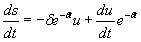
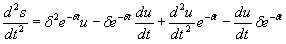
После нахождения первой и второй производных и их подстановки в (1) получим
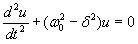
Решение уравнения зависит от знака коэффициента перед искомой величиной. Пусть этот коэффициент положителен:
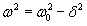(7.2)
Тогда получим уравнение решением, которого является функция u=A0cos(ωt+φ). Значит, решение уравнения (7.1) в случае малых затуханий
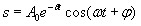где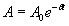 
Период затухающих колебаний с учетом формулы (7.2) равен
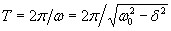
Если A(t) и A(t+Т) — амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение
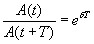
называется декрементом затухания, а его логарифм
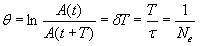
— логарифмическим декрементом затухания; Ne — число колебаний, совершаемых во время уменьшения амплитуды в е раз. Логарифмический декремент затухания — постоянная для данной колебательной системы величина.
Для характеристики колебательной системы пользуются понятием добротности, которая при малых значениях логарифмического декремента равна
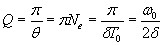
Из формулы следует, что добротность пропорциональна числу колебаний Nе, совершаемых системой за время релаксации.
Для пружинного маятника массой m, совершающего малые колебания под действием упругой силы F=-kx, сила трения пропорциональна скорости, т. е.
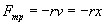
где r — коэффициент сопротивления; знак минус указывает на противоположные направления силы трения и скорости.
При данных условиях закон движения маятника будет иметь вид
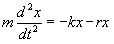
Используя формулу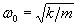 
и принимая, что коэффициент затухания 
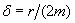получим дифференциальное уравнение затухающих колебаний маятника:
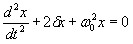
Колебания маятника подчиняются закону
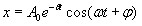где частота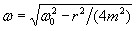 
Коэффициент затухания. Коэффициент d, определяющий быстроту изменения амплитуды, называется коэффициентом затухания. Если промежуток времени Dt = 1/d, то А0/А = е. Отсюда вытекает физический смысл коэффициента затухания:
величина 1/d, равна промежутку времени, по истечении которого амплитуда колебаний уменьшается в е = 2.73 раз.
Добротность пружинного маятника
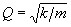
При увеличении коэффициента затухания δ период затухающих колебаний растет и при δ = ω0 обращается в бесконечность, т. е. движение перестает быть периодическим. В данном случае колеблющаяся величина асимптотически приближается к нулю, когда t→∞. Процесс не будет колебательным. Он называется апериодическим.
Логарифмический декремент затухания - безразмерная характеристика затухающих колебаний, измеряемая натуральным логарифмом отношения двух последовательных максимальных отклонений колеблющейся величины в одну и ту же сторону.
Добротность — характеристика колебательной системы, определяющая остроту резонанса и показывающая, во сколько раз запасы энергии в реактивных элементах контура больше, чем потери энергии на активных элементах за один период колебаний.
Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии в течение каждого периода. Колебания в системе с высокой добротностью затухают медленно.
Общая формула для добротности любой колебательной системы:
,
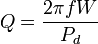где:
f — частота колебаний
W — энергия, запасённая в колебательной системе
Pd — рассеиваемая мощность.