Независимое множество вершин

Учебно-МЕТОДИЧЕСКое пособие

ПО ДИСЦИПЛИНЕ

«ТЕОРИЯ ГРАФОВ»

Донецк 2010

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И ИСКУССТВЕННОГО

ИНТЕЛЛЕКТА

Учебно-МЕТОДИЧЕСКое пособие

ПО ДИСЦИПЛИНЕ

«ТЕОРИЯ ГРАФОВ»

для студентов специальностей

«Программное обеспечение автоматизированных систем»,

«Интеллектуальные системы принятия решений»

дневной формы обучения

Утверждено:

на заседании кафедры программного

обеспечения интеллектуальных систем

(протокол № 9 от 21.05.2010г.)

на заседании Ученого совета ГУИиИИ

(протокол № 9 от 31.05.2010г.)

Донецк-2010

Учебно-методическое пособие по дисциплине «Теория графов» для студентов специальностей «Программное обеспечение автоматизированных систем» и «Интеллектуальные системы принятия решений» дневной формы обучения /Сост.: Е.В. Бычкова, Т.В. Ермоленко, Донецк: ГУИиИИ, 2010.- 108 с.

Изложены теоретические основы по следующим разделам теории графов: подграфы, изоморфизм, маршруты и связность, деревья и остовы, основы цикломатики, орграфы. Содержатся рекомендации по изучению теоретического материала, контрольные вопросы, рекомендуемая литература, задания для лабораторных работ и примеры их выполнения.

Составители:

ст. преп. Е.В. Бычкова,

асс. Т.В. Ермоленко

Рецензент: с.н.с., к.ф.-м.н., И.С. Грунский

ВВЕДЕНИЕ В ТЕОРИЮ НЕОРИЕНТИРОВАННЫХ ГРАФОВ

СВЕДЕНИЯ ИЗ ИСТОРИИ

1736 г. считается годом возникновения теории графов: Л.Эйлер опубликовал результаты решения задачи о Кенигсбергских мостах и сформулировал критерий существования в графах специального маршрута (эйлерова цикла). Более чем 100 лет эти результаты оставались единственными и лишь в середине XIX в.инженер-электрик Г. Кирхгоф разработал теорию деревьев для исследования электрических цепей. Математик А. Кэли решил перечислительные задачи для определенных типов деревьев при исследовании строения углеводородов. К этому же периоду относится появление знаменитой проблемы 4 красок.

За последние десятилетия теория графов превратилась в один из некоторых бурно развивающихся разделов математики. В теоретико-графовых терминах формулируется большое число задач, связанных с дискретными объектами.

Термин “граф”был введен в 1936 г. венгерским математиком Д. Кенигом.

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

Пусть имеется некоторое множество V¹Æ и пусть V⁽²⁾ – неупорядоченное множество всех его двухэлементных подмножеств (V⁽²⁾ ={(u,v): u,vÎV, неупорядоченная пара}). Тогда неориентированным графом G называется пара множеств (V,E), где 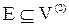. Обозначается: G=(V,E).

Множество V называется множеством вершин графа, а множество Е – множеством ребер графа.

Число |V| вершин графа G называется его порядком. Если 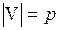, а , то граф G=(V,E) называют p-графом, или (p,q)-графом,или G _{p, q}.

Пример: 4-граф, или (4,5)-граф, или G _{4, 5}.

Две вершины графа называются смежными, если они соединены ребром.

Два ребра графа называются смежными, если они имеют общую вершину.

Обозначим ребро графа: e=(u,v), где u и v –концевые вершины ребра. Ребро e инцидентно вершине v, если вершина v является одной из концевых вершин ребра e.

Заметим, что смежность есть отношение между однородными элементами графа, тогда как инцидентность является отношением между разнородными элементами.

Если множество V конечно, то граф называют конечным. Далее будем говорить только о конечных графах.

СПОСОБЫ ЗАДАНИЯ ГРАФОВ

Существуют следующие основные способы задания графов.

1. Перечисление множеств V (вершин) и E (ребер), задающих граф.G=(V, E).

2. Графический: множество вершин V – это множество точек плоскости, множество ребер Е – множество отрезков прямой(кривой) на плоскости.

3. Матричные способы описания.

Пусть G=(V,E), 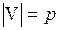, а , тогда:

a) матрица смежности – квадратная матрица 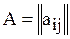, , 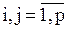где

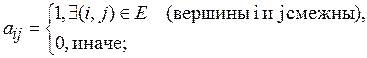
b) матрица инцидентности –прямоугольная матрица 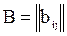, , 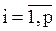, 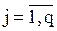где

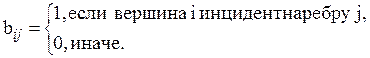
Пример: Задан граф G=(V, E),где V={v₁,v₂, v₃, v₄}, E={v₁v₂, v₂v₃, v₁v₃, v₁v₄, v₃v₄}={e₁, e₂, e₃, e₄, e₅}.

A – матрица смежности:	B – матрица инцидентности:

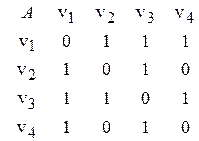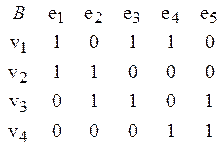СТЕПЕНИ ВЕРШИН ГРАФА

Окружением вершины v называется множество всех вершин графа G, смежных с ней; обозначается: N(v).

Степенью или валентностью вершины v неориентированного графа G называется число ребер, инцидентных данной вершине (число вершин в ее окружении). Обозначается: deg(v) ( ).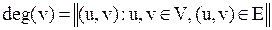

Число DG = max deg(v), 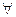vÎV называется максимальной степенью графа G, а число d(G) = min deg(v), 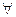vÎV – минимальной степеньюграфа G.

Пример:

deg(v₁)= deg(v₃)=3; deg(v₂)= deg(v₄)=2.

DG =3, d(G) = 2.

Вершина v графа G называется изолированной, если ее степень равна нулю (deg(v)=0).

Вершина v графа G называется висячей или концевой, если степень этой вершины равна единице (deg (v)=1).

Вершина v графа G(p,q) называется доминирующей, если ее степень равна p-1 (deg (v)=p-1).

Пример:

доминирующей вершины нет;

висячая – v₃;

изолированная – v₅.

Лемма о рукопожатии. Сумма степеней всех вершин графа четна и равна удвоенному числу ребер:

.

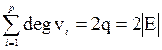Следствие.В любом графе число вершин с нечетной степенью четно.

ОПЕРАЦИИ НАД ГРАФАМИ

Рассмотрим графы 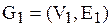и .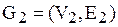

Объединением двух графов 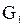и 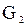называется граф G, множество вершин которого 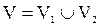и множество ребер .

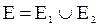Пример:

Пересечение двух графов 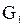и 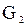– это граф G, у которого множество вершин 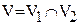и множество ребер .

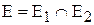Пример:

Непересекающимися графами называются графы 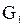и 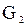такие что 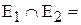Æ и 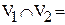Æ (нет общих ребер и нет общих вершин).

Пусть задан граф G=(V,E) и 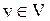, тогда удаление вершины – это унарная операция над графом G, заключающаяся в построении порожденного подграфа G\{v} графа G на множестве вершин V\{v} (вершина удаляется из графа вместе с инцидентными ей ребрами).

Пример: v=v₂

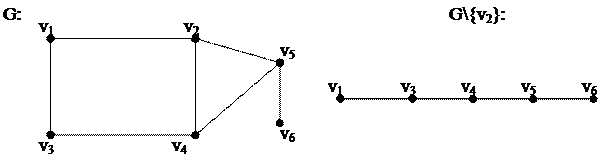
Пусть , тогда удаление ребра - это унарная операция над графом G, заключающаяся в построении порожденного подграфа G\{e} графа G с тем же множеством вершин и множеством ребер .

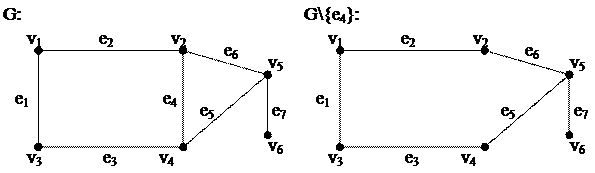
Пример: e=e₄

Говорят, что пара вершинv_i и v_j в графе G замыкается (отождествляется), если они заменяются такой новой вершиной, что все ребра графа G, инцидентные вершинам v_i и v_j, становятся инцидентными этой новой вершине.

Пример:

Стягивание заключается в удалении ребра e и отождествлении его концевых вершин.

Пример:

СПЕЦИАЛЬНЫЕ ГРАФЫ

В общем случае во множестве Е допускается более чем одно ребро с одинаковыми концевыми вершинами. Такие ребра называются параллельными, или кратными.

Ребро, соединяющее вершину v саму с собой, называется петлей.

Граф, содержащий кратные ребра, но не содержащий петель, называется мультиграфом.

Пример:

Граф, содержащий и петли, и кратные ребра, называется псевдографом.

Пример:

Граф, не содержащий ни одного ребра, называется пустым графом и обозначается 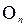, где n – количество вершин графа.

Пример: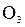

Граф, не содержащий ни одного ребра и ни одной вершины, называется
0-графом(нуль-графом).

Тривиальный граф – это граф (1,0).

Граф, G называется полным, если у него все вершины смежные между собой. Каждая вершина полного графа является доминирующей. Обозначается: K_p, где p – количество вершин.

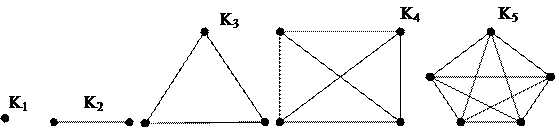Пример:

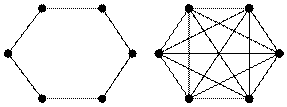Однородным, илирегулярным, называется граф, у которого степени всех вершин равны. Все полные графы являются однородными.

Пример:

ПОДГРАФЫ

Неориентированный граф G=(V,E) называется помеченным, или перенумерованным, если каждой вершине графа поставлена в соответствие уникальная метка (число, символ); в противном случае граф называется абстрактным.

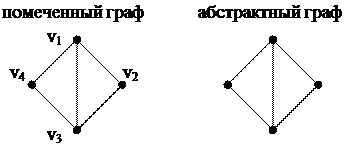Пример:

Граф 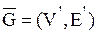называется дополнением графа G, если множества вершин графов 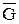и G совпадают, т. е. 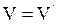, а множество ребер 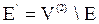. Следовательно, любые две вершины, смежные в графе G, не смежны в его дополнении .

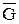Пример:

Подграфомграфа G называется такой граф 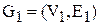, у которого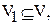

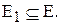
Пример: подграфы графа G

Остовным подграфомграфа G называется такой подграф, у которого множество вершин равно множеству вершин исходного графа, а множество ребер может составлять часть множества ребер исходного графа ( ).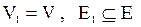

Пример: остовные подграфы графа G

Порожденным подграфам графа G (подграфом, порожденным множеством вершин 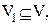) называется подграф 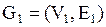такой что содержит все ребра, инцидентные вершинам из множества 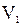( т.е. те вершины, которые соединены в исходном графе ребром, будут соединены ребром и в порожденном подграфе).

Пример: подграфы графа G, порожденные вершинами

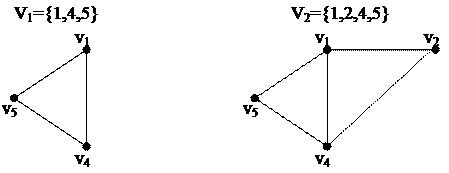
ДВУДОЛЬНЫЕ ГРАФЫ

Граф, G=(V,E) называется двудольным,илибиграфом, если множество его вершин V можно разбить на два подмножества V₁ и V₂, такие что любое ребро графа имеет одну концевую вершину во множестве V₁ и другую во множестве V₂. Таким образом, 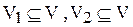, V₁ÇV₂=Æ, V₁ÈV₂=V.

Пример: двудольный граф

Если в двудольном графе G с разбиением (V₁,V₂) 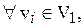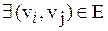, то такой двудольный граф называется полным двудольным графом.

Обозначается: 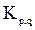, где .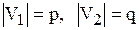

Пример:

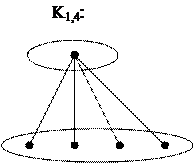Полный двудольный граф К_1,n называется звездой.

Пример:

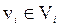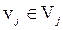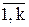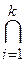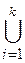Граф G=(V,E) называется k-дольным, если множество вершин V можно разбить на k непересекающихся подмножеств таких что каждое ребро графа, имеющее концевую вершину , имеет другую концевую вершину (i¹j), i,j= , V_i=Æ, V_i=V.

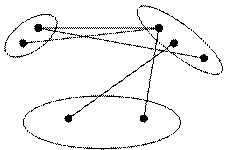Пример:

ИЗОМОРФИЗМ ГРАФОВ

Два графа G и Н называют изоморфными ( 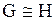), если существует взаимооднозначное соответствие (биекция) между множествами их вершин, сохраняющее отношение смежности.

Пусть G=(V,E), 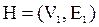. Тогда 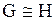, если

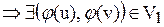и наоборот.

Пример:

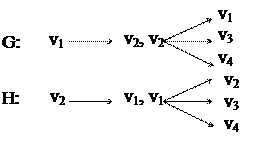
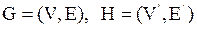
V	v1	v2	v3	v4
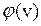	v2	v1	v3	v4

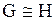
Пример изоморфных графов:

Условия изоморфизма графов:

- совпадение количества вершин и ребер;

- соответствие распределения степеней вершин;

- биекция, сохраняющая отношение смежности между вершинами графов.

Примеры неизоморфных графов:

НЕЗАВИСИМОЕ МНОЖЕСТВО ВЕРШИН

Независимым множеством вершин графа G, или внутренним устойчивым множеством, называется такое множество вершин S графа G, что любые две вершины этого множества не смежны.

Подграф, порожденный независимым множеством, является пустым.

Независимое множество называется максимальным (Q), если оно не является собственным подмножеством другого независимого множества.

Независимое множество называется наибольшим, если оно наибольшее по мощности среди всех независимых множеств. Мощность наибольшего независимого множества называется числом независимости; обозначается: .

Пример:

независимые множества:

S1={v1,v3}	S6={v2,v8}	S11={v1,v4}	S16={v7,v8}	S21={v3,v7,v8}
S2={v3,v6}	S7={v2,v7}	S12={v4,v6}	S17={v2,v4,v8}	S22={v5,v7,v8}
S3={v3,v8}	S8={v3,v7}	S13={v1,v5}	S18={v1,v3,v7}	S23={v2,v7,v5}
S4={v5,v8}	S9={v4,v8}	S14={v1,v7}	S19={v1,v5,v7}	S24={v2,v7,v8}
S5={v2,v4}	S10={v2,v5}	S15={v5,v7}	S20={v2,v8,v5}	S25={v2,v5,v7,v8}

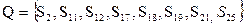, наибольшее – , .

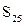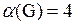КЛИКА

Кликойграфа G называется такое подмножество вершин исходного графа, что любые две его вершины смежны.

Подграф, порожденный кликой, является полным.

Максимальной кликой графа G называется клика, не являющаяся собственным подмножеством другой клики с большим числом вершин.

Клика графа G называется наибольшей, если число вершин в ней является максимальным среди всех других клик.

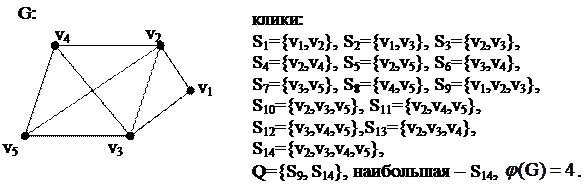Мощность наибольшей клики называется кликовым числом, или плотностью графа; обозначается: .

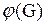Пример:

ДОМИНИРУЮЩИЕ МНОЖЕСТВА

Доминирующим,иливнешним устойчивым множеством графа G, называется подмножество вершин исходного графа S такое что:

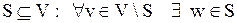такая что .

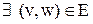Доминирующее множество называется минимальным, если нет другого доминирующего множества, содержащегося в нем.

Наименьшее доминирующее множество - доминирующее множество с наименьшей мощностью.

Мощность наименьшего доминирующего множества называется числом доминирования; обозначается: .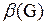

Пример:

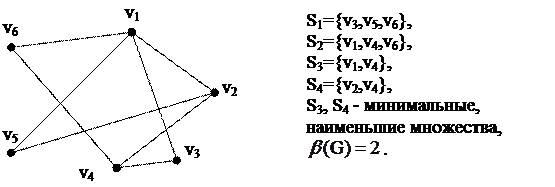Ядромграфа называется множество вершин графа, которое является одновременно и независимым, и доминирующим множеством.

Не каждый граф содержит ядро, например:

Граф K_2,2 имеет два ядра:

Контрольные вопросы

1. Определение неорграфа, подграфа, остовного и порожденного подграфов.

2. Дополнение к графу.

3. Операции над графами.

4. Изоморфизм графов.

5. Помеченные и абстрактные графы.

6. Клика. Максимальная и наибольшая клика. Кликовое число, или плотность графа.

7. Независимое множество. Максимальное и наибольшее независимое множество. Число независимости.

8. Полный граф. Число ребер в полном графе.

9. Доминирующее множество. Минимальное и наименьшее доминирующие множество. Число доминирования.

10. Ядро графа.