Частотні характеристики імпульсних систем

Частотні характеристики імпульсних систем можна отримати за дискретними передавальними функціями за допомогою підстановки 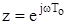, яка аналогічна підстановці s = jw для частотних характеристик безперервних систем: 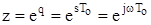. Під час побудови частотних характеристик часто використовують відносну частоту 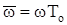і підстановку .

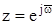Амплітудно-фазова частотна характеристика імпульсної розімкнутої системи визначається за формулою:

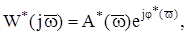(8.44)

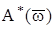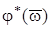де і - амплітудна частотна і фазова частотна характеристики розімкнутої системи.

За формулами Ейлера для комплексних чисел: 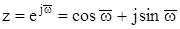. Тому частотні характеристики імпульсних систем на відміну від безперервних є періодичними функціями частоти. Оскільки w = 2p/Т₀, то відносна частота дорівнює 2p, а значить, частотні функції імпульсних систем та їх характеристики повністю визначаються змінюванням відносної частоти 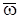в інтервалі 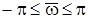або .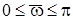

Частотні характеристики імпульсної системи дають інформацію про реакцію на гармонічні дії та застосовуються для дослідження стійкості та якості систем.

Приклад 8.6 Побудувати амплітудну частотну характеристику розімкнутої імпульсної системи (рис. 8.6), що складається з імпульсного елемента і безперервної частини з передавальною функцією W_п(s) = k/(Ts+1). Імпульсний елемент генерує короткі прямокутні імпульси тривалістю gТ₀, де g<<1.

Згідно з (8.39) дискретна передавальна функція має вигляд:

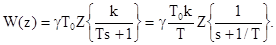
Згідно з табл. 8.1 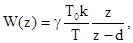де .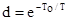

Виконуємо підстановку 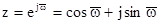. Помноживши чисельник і знаменник передавальної функції 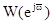на комплексно-спряжене число, звільнимося від уявного числа у знаменнику:

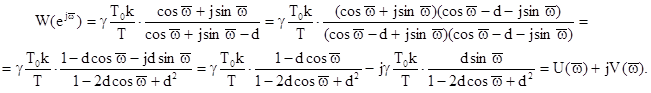Тоді амплітудна частотна функція:

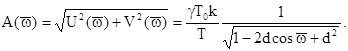
Характеристики для значень k = 400; T = 1c; g =0.05, Т₀=0,05с і Т₀ = 1,5с наведені на рис. 8.7.

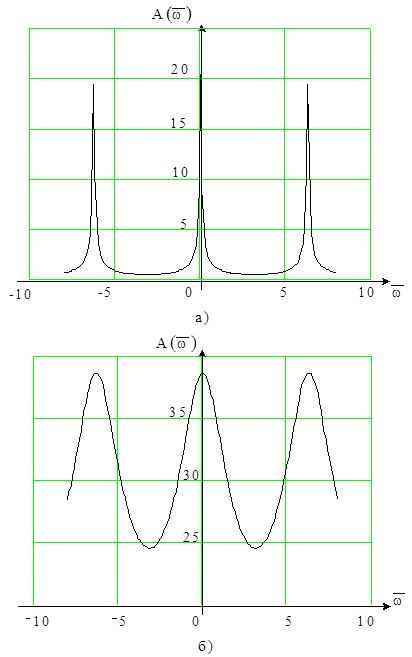
Рис. 8.7 – Амплітудні частотні характеристики імпульсної

системи за умови Т₀=0,05с (а), і Т₀ = 1,5с (б)

У першому випадку (рис. 8.7, а) частота квантування перевищує смугу пропускання безперервної частини системи, а в другому (рис. 8.7, б) знаходиться у цій смузі.

У граничному випадку, коли частота квантування нескінченно велика, вхідний гармонічний сигнал сприймається системою як безперервний і частотні характеристики імпульсної системи збігаються з частотними характеристиками безперервної частини системи. Якщо частота квантування досить висока, але не нескінченно велика, характеристики імпульсної системи є характеристиками безперервної частини системи, які періодично повторюються з частотою 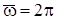(рис. 8.7, а). Отже, як зазначалося раніше (п. 8.2), при досить високих частотах імпульсна система є еквівалентною безперервній системі.

Під час побудови частотних характеристик імпульсних систем відносну частоту 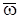достатньо змінювати у межах від 0 до p, а для побудови характеристик безперервних систем частоту змінюють від 0 до ¥. Це створює певні незручності під час дослідження дискретних систем за методами, що розроблені для безперервних систем. Тому часто використовують білінійне w-перетворення дискретних передавальних функцій, відповідно до якого аргумент z замінюють на аргумент w за допомогою підстановки:

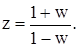(8.45)

Тоді з урахуванням, що 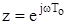, отримуємо:

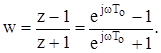(8.46)

Ділимо чисельник і знаменник цього виразу на :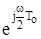

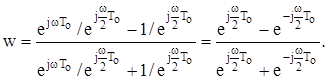
Згідно з формулою Ейлера для комплексних чисел отримуємо:

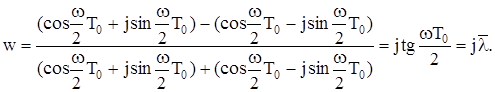(8.47)

Величина 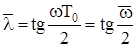називається відносною псевдочастотою. Вона пов’язана з частотою w формулами:

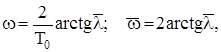(8.48)

з яких видно, що змінюванню частоти 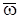від 0 до p відповідає змінювання псевдочастоти від 0 до ¥.

Під час побудови частотних характеристик зручніше користуватися абсолютною псевдочастотою:

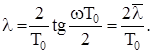(8.49)

При малих частотах 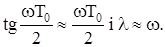Тому за умови wТ₀ < 2 у розрахунках псевдочастоту можна замінити дійсною коловою частотою w.

Під час побудови частотних характеристик відносно псевдочастоти l за дискретною передавальною функцією W(z) спочатку від аргументу z за (8.45) переходять до аргументу w, а потім виконують підстановку 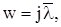або 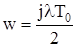і отримують комплексну передавальну функцію:

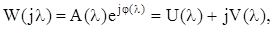(8.50)

за якою будують АФХ або логарифмічні амплітудну і фазову характеристики L(l) і j(l). Ці характеристики визначають за формулами, аналогічними до формул для безперервних систем:

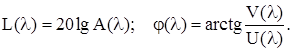(8.51)

Так само, як і для безперервних систем, L(l) вимірюється у децибелах, j(l) – у градусах або радіанах, lg(l) – у декадах.

Логарифмічні частотні характеристики імпульсних систем будувати складніше порівняно з безперервними. Це зумовлено тим, що при послідовному з’єднанні безперервних ланок без імпульсних елементів дискретна передавальна функція не дорівнює добутку дискретних передавальних функцій окремих ланок і вираз W(jl) звичайно є сумою дробів. Тому перед побудовою характеристик комплексну передавальну функцію спочатку необхідно подати у вигляді дробу, що містить у чисельнику і знаменнику елементарні співмножники вигляду k, jl, Tjl+1, T²(jl)²+2xTjl+1. Після цього можна будувати асимптотичну ЛАХ дискретної системи таким самим способом, як і для безперервних систем. ЛФХ визначається як сума фазових характеристик, що відповідають елементарним співмножникам передавальної функції.

Частотна характеристика розімкнутої системи має скінчене значення при 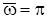, тому при 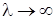ЛАХ прямує до сталої величини, а ЛФХ – до значення j(l) = 0 або j(l) = -180⁰.

Застосування псевдочастоти і логарифмічних характеристик дає змогу досліджувати імпульсні системи і виконувати синтез коректувальних пристроїв методами, що розроблені для безперервних систем.

Приклад 8.7 Розрахувати і побудувати логарифмічну амплітудну характеристику розімкнутої імпульсної системи, дискретна передавальна функція якої має вигляд:

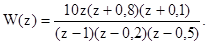
Виконуємо w-перетворення за допомогою підстановки (8.45) і після спрощень отримуємо:

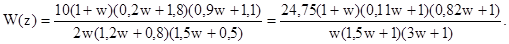
Виконуємо підстановку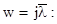

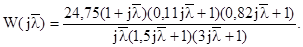
Методика побудови 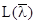така сама, як і для побудови асимптотичних ЛАЧХ безперервних систем:

- ліворуч першої частоти спряження 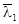низькочастотна асимптота ЛАЧХ проходить у напрямку точки з координатами ( 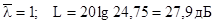) з нахилом –20 дБ/дек (знаменник передавальної функції має співмножник );

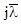- частоти спряження: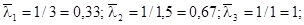

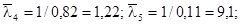
- у частотах спряження 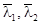нахил ЛАЧХ змінюється на –20 дБ/дек, а в частотах 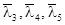- на +20 дБ/дек.

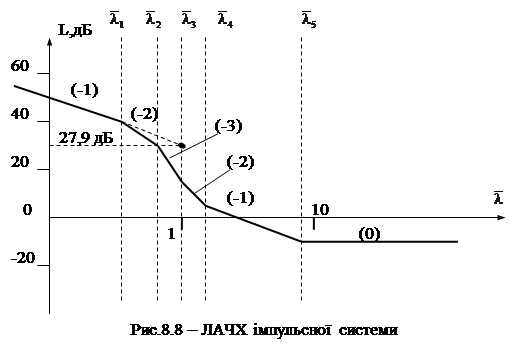
ЛАЧХ системи наведена на рис. 8.8.