Функция одной и нескольких переменных

МОДУЛЬ 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

ЛЕКЦИЯ 2.1. ПЕРЕМЕННАЯ ВЕЛИЧИНА. ФУНКЦИЯ ОДНОЙ И НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. СПОСОБЫ ЗАДАНИЯ. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ, ПРЕДЕЛ ПЕРЕМЕННОЙ ВЕЛИЧИНЫ, ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ, ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ, ОДНОСТОРОННИЕ ПРЕДЕЛЫ

Прогнозируемые результаты обучения в виде составляющих предметных компетенций:

· Базовые понятия:

-– функция одной и нескольких переменных,

– способ задания функции,

– предел последовательности,

– предел функции в точке,

– односторонние пределы,

· Базовые операции:

– определение способа задания функции одной и нескольких переменных,

– распознавание вида неопределенности.

При чтении лекции используется объяснительно-иллюстративный метод, позволяющий ввести студентов в понятийно-категориальный аппарат данного раздела математики.

Ориентация на развитие компетенций:

ОК-5 – способность к самоорганизации и самообразованию;

ПК-1 – способность к анализу и синтезу;

ПК – 8: способность использовать информационные средства и технологии при решении задач, возникающих в ходе профессиональной деятельности;

ОПК-4 – готовность сочетать теорию и практику для решения инженерных задач.

Переменная величина

Понятие «величина» – основное понятие, с которым мы встречаемся в любой естественнонаучной или технической области знания. Под величинойпонимают все то, что может быть измерено и выражено числом (числами). Например, длина, площадь, объем, вес, температура, скорость, сила и т. п.

Обычно, среди совместно рассматриваемых величин некоторые изменяются, другие же остаются постоянными.

Переменной величиной называют величину, которая принимает различные численные значения; величина, которая сохраняет одно и тоже численное значение, называется постоянной.

Переменная величина считается заданной, если задана совокупность её значений. Совокупность значений переменной величины называется областью изменения переменной величины.

Переменные величины делятся на два класса: непрерывные и дискретные.

Переменная величина называется непрерывной, если областью её изменения является некоторый интервал. Переменная величина называется дискретной, если областью её изменения является множество изолированных точек. Например, скорость ветра – непрерывная величина, число студентов в аудиториях – дискретная величина.

Переменная величина называется упорядоченной, если из двух значений переменной величины можно указать предыдущую и последующую.

Если переменная величина в области изменения убывает или возрастает, то она называется монотонной.

Если значения переменной величины таковы, что число 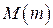будет больше (меньше) любого значения переменной величины, то говорят, что переменная величина ограниченна сверху (снизу). Переменная величина называется ограниченной, если она ограничена сверху и снизу.

Функция одной и нескольких переменных

Чаще всего изменению одной переменной величины сопутствует изменение другой, более того, изменение одной является причиной изменения другой. В некоторых случаях изменение одной переменной величины может быть продиктовано изменением двух, трех и более величин.

Примеры.

1.Площадь квадрата 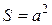изменяется в зависимости от изменения длины его стороны .

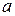2. Работа, совершаемая на некотором прямолинейном участке пути под действием некоторой силы, 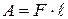изменяется в зависимости от изменения длины участка 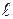и величины силы воздействия .

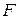3. Периметр треугольника 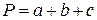изменяется в зависимости от длин его сторон 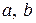и .

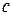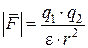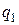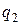4. Сила взаимодействия двух электрических зарядов по закону Кулона изменяется в зависимости от изменения величин зарядов и , значения диэлектрической проницаемости 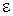и расстояния между зарядами .

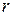Таким образом, всякий процесс характеризуется взаимоизменяемостью нескольких переменных величин. Такое представление приводит к важнейшему в математике понятию функциональной зависимости, т.е. связи между переменными величинами. Важнейшей задачей математического анализа является всестороннее изучение функциональных зависимостей.

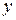Пусть даны и – переменные величины, 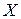и – области изменения этих величин.

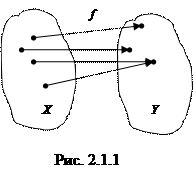Определение. Если каждому значению величины 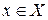по некоторому закону соответствует единственное значение величины 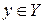, то говорят, что задана функция , или что величины и 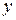связаны между собой функциональной зависимостью (см. рис. 2.1.1).

При этом, – аргумент функции (независимая переменная), 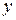– значение функции (зависимая переменная), 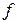– закон соответствия, – функция одной независимой переменной.

Множество 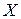называется областью определения функции и обозначается 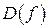. Множество 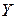называется областью значений функции и обозначается .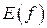

Иногда функциональную зависимость 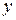от пишут в виде 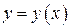, не вводя новой буквы 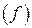для обозначения зависимости.

Исходя из определения, областью определения функции , является множество значений , при которых функция имеет смысл.

Для функции одной переменной областью определения 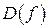является интервал координатной оси 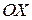или вся координатная ось.

Пример. Для функци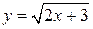и найти 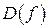и изобразить её.

Решение: .

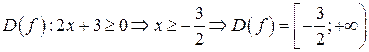Ответ: .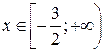

Пусть даны 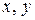и 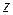– переменные величины, 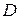– область изменения пар чисел 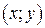, а 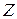– область изменения .

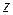Определение.Если каждой паре чисел 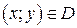по некоторому закону соответствует единственное значение величины 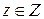, то говорят, что задана функция 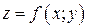(см. рис. 2.1.2).

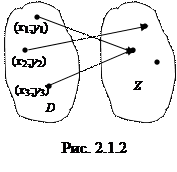При этом 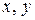– аргументы функции (независимые переменные), 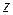– значение функции (зависимая переменная), 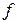– закон соответствия, 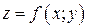– функция двух независимых переменных, 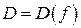– область определения функции, 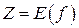– область значений функции.

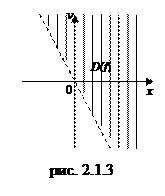Для функции двух переменных 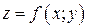область определения 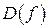является часть координатной плоскости 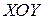или вся координатная плоскость.

Пример. Для функци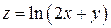и найти 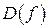и изобразить ее.

Решение: 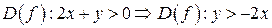. Значит, областью определения является часть плоскости 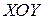, координаты точек которой удовлетворяют неравенству 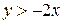, т.е. полуплоскость, расположенная выше прямой 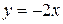. Так как точки прямой не удовлетворяют неравенству 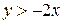, то прямая изображается пунктирной линией (см. рис.2.1.3).

Ответ: .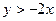

Определение. Если каждой совокупности переменных величин 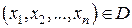по некоторому закону соответствует единственное значение 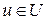, то говорят, что задана функция 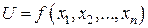– функция 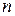независимых переменных.

Для функции трех переменных 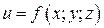область определения функции геометрически представляется в виде части трехмерного пространства.

Для функции 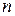переменных, при 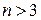, область определения невозможно представить геометрически.

Способы задания функции

Наиболее распространены следующие способы задания функции: аналитический, графический и табличный.

I. Аналитический способ задания функции состоит в том, что дается формула, с помощью которой по значениям независимой переменной (независимых переменных) можно получить соответствующие им значения функции.

Функция, заданная аналитическим способом может быть задана: явно, неявно и параметрически.

Функция называется явно заданной, если она задана уравнением 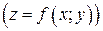, разрешенным относительно зависимой переменной 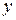(зависимой переменной ).

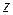Примеры.

1. 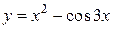– явная функция одной переменной.

2. 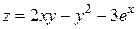– явная функция двух переменных.

Функция называется неявно заданной, если она задана уравнением 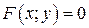– для функции одной переменной ( 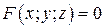– для функции двух переменных), не разрешенным относительно зависимой переменной 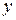(зависимой переменной ).

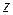Аналогично определяется неявно заданная функция 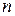независимых переменных вида 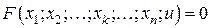, где .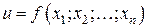

Примеры.

1. 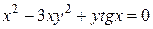– неявно заданная функция одной переменной.

2. 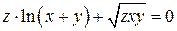– неявно заданная функция двух переменных.

3. 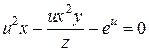– неявно заданная функция трех переменных.

Функция называется параметрически заданной, если сама функция и её аргумент (аргументы) заданы аналитическими выражениями, зависящими от одного и того же параметра :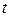

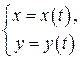– функция одной переменной; 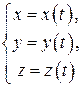– функция двух переменных.

Исключая параметр, можно получить функцию явно или неявно заданную.

Пример. 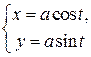– параметрически заданная функция одной переменной. Исключим параметр :

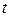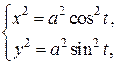
тогда 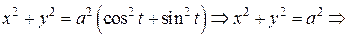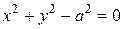– неявно заданная функция одной переменной.

Преимущества аналитического способа задания функции заключаются: – в сжатости, компактности задания;

– в возможности применить к данной функции аппарат математического анализа, поскольку он наилучшим образом приспособлен к аналитической форме задания функций.

II. Графический способ задания функции состоит в построении графика этой функции.

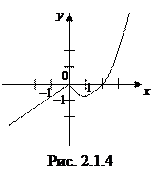Определение. Графиком функции называется геометрическое место точек, координаты которых удовлетворяют уравнению .

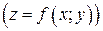Графиком функции одной переменной является линия на плоскости.

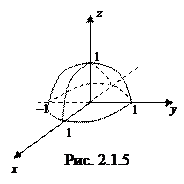Пример. Функция 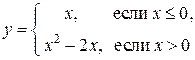изображена в виде графика (рис. 2.1.4).

Графиком функции двух переменных 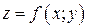является поверхность в трехмерном пространстве.

Пример. Графиком функции 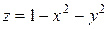является поверхность второго порядка – эллиптический параболоид (рис. 2.1.5).

К графику функции не может быть непосредственно применен аппарат математического анализа. Наряду с этим недостатком, график функции обладает весьма важным преимуществом – наглядностью, что делает его чрезвычайно полезным при изучении функции .

III. Табличный способ задания функции состоит в перечислении значений независимой (независимых) переменной (переменных) и соответствующих им значений функции, с последующим занесением их в таблицу:

Таблица 2.1.1

			…
			…

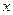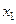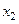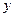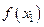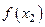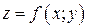
Таблица 2.1.2

				…
				…
				…
				…

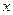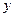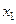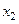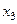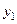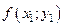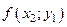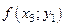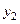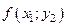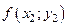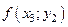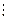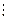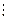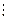Все вышеприведенные определения, относящиеся к случаю функции двух независимых переменных, без существенных изменений переносятся на случаи функции многих независимых переменных. Заметим только, что геометрическая иллюстрация функций от 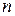независимых переменных при 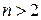теряет наглядность.

Основные свойства функции

Изучить заданную функцию – это значит охарактеризовать ход её изменения при изменении независимой переменной.

Функции многих переменных, с которыми приходится иметь дело в инженерной практике, по своим свойствам, за исключением некоторых, мало отличаются от функций одной переменной. Поэтому рассмотрим основные характеристики поведения функции на примере функции одной переменной.

Определение. Нулем функции называют такое значение , при котором .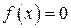

В интервале положительного знакафункции график расположен выше оси 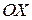, в интервале отрицательного знака – ниже оси 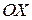, в нуле функции график пересекает ось .

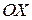Пример.Найти точки пересечения графика функции 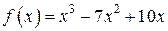с осью .

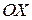Решение: Ордината точки пересечения графика функции с осью 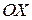равна нулю, т.е. 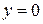. Значит абсцисса точки пересечения – есть нуль функции. Используя определение, получаем:

;

,

.

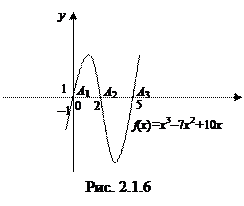
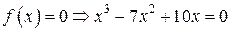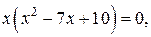
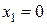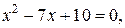
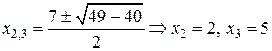Таким образом, нули функции: 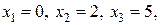а точки пересечения графика функции с осью 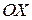: 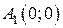, , 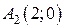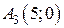(рис. 2.1.6).

Определение. Промежутком, симметричным относительно начала координат, называется промежуток, которому вместе со значением принадлежит противоположное ему значение: .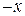

Определение. Функция , заданная на симметричном относительно начала координат промежутке, называется четной, если для любого значения из этого промежутка выполняется равенство .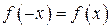

График четной функции симметричен относительно оси 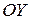(см. рис. 2.1.7).

y

Определение. Функция , заданная на симметричном относительно начала координат промежутке, называется нечетной, если для любого значения из этого промежутка выполняется равенство .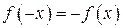

График нечетной функции симметричен относительно начала координат (см. рис. 2.1.8).

Сумма и разность двух четных (нечетных) функций есть функция четная (нечетная).

Произведение двух четных или двух нечетных функций есть функция четная, а произведение четной функции на нечетную – нечетная функция.

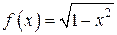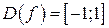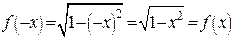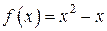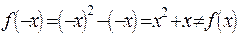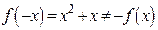Пример. Функция – четная, так как в области определения выполняется равенство . А функция – ни четная, ни нечетная, так как на всей числовой оси и , где .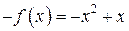

Определение. Функция называется периодической, если существует число 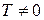такое, что для любого значения из области определения функции выполняется равенство 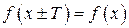, где 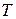– наименьший положительный период.

Если 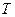– наименьший положительный период функции, то число 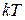, где 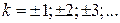– также является периодом функции.

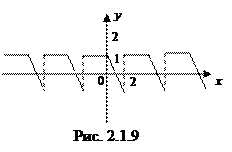Пример. Наименьшим положительным периодом функци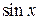й и 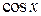является число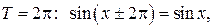 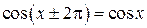, а для функци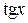й и 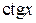это число .

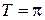Из определения периодической функции следует, что её график будет «повторять» себя через промежуток равный по длине наименьшему положительному периоду 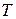. Поэтому достаточно построить график такой функции на любом промежутке вида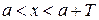 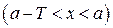. Смещая построенный график вдоль оси 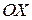на отрезке длины 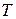, получим график функции .

Пример. График функции

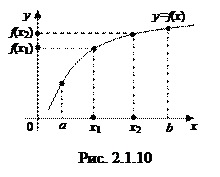
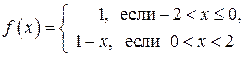– периодической, с наименьшим положительным периодом 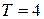(см. рис.2.1.9).

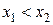Определение. Функция называется возрастающей на некотором интервале, если большим значениям аргумента соответствуют большие значения функции, т.е. если , то 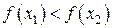(см. рис. 2.1.10).

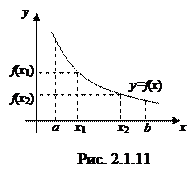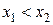Определение. Функция называется убывающей на некотором интервале, если большим значениям аргумента соответствуют меньшие значения функции, т.е. если , то 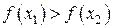(см. рис. 2.1.11).

Возрастающие и убывающие функции называются монотонными функциями. Интервал, на котором функция возрастает (убывает) называется интервалом возрастания (убывания) функции или интервалом монотонности.

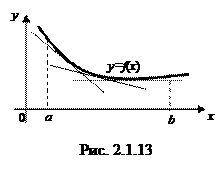
Определение.График функции называется выпуклым (вогнутым) на некотором интервале, если касательная, проведенная к графику функции в любой точке с абсциссой из этого интервала, расположена выше (ниже) графика функции (см. рис. 2.1.12, 2.1.13).

Определение. Функция называется ограниченной, если существует такое число 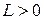, что для всех 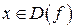выполняется неравенство .

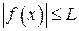График ограниченной функции лежит между прямыми 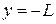и .

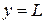Определение. Значение функции, большее (меньшее) всех других её значений в некотором интервале, называется наибольшим (наименьшим) значением функции в этом интервале.

Ограниченная на некотором отрезке функция принимает на этом отрезке свое наибольшее и наименьшее значения.

Определение. Пусть задана функция с областью определения 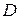и областью значений 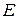. Если каждому значению 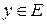соответствует единственное значение 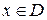, то определена функция 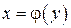, обратная к функции , с областью определения 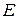и областью значений .

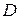Про функции и 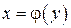говорят, что они являются взаимно обратными. Чтобы найти функцию 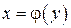достаточно решить уравнение 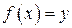относительно (если это возможно).

Примеры.

1.Для функции 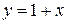обратной является функция .

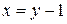2.Для функции 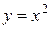на интервале 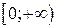обратная функция существует и имеет вид 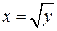, а на интервале 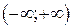не существует, так как одному значению 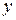соответствует два значения .

Если необходимо построить графики взаимно обратных функций так, чтобы ось 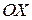была осью аргумента, надо обозначить аргумент в обратной функции через , а функцию через 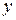, т.е. функция примет вид .

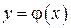График обратной функции 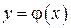симметричен с графиком функции относительно биссектрисы первого и третьего координатных углов (см. рис. 2.1.14).

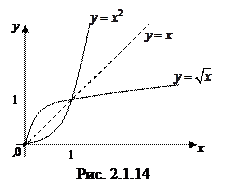Геометрически ясно, что только монотонная функция имеет обратную, однозначную функцию.

Определение. Пусть функция 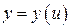определена на множестве 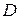, а функция 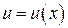на множестве 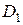, причем для любого 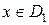, соответствующее значение 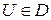. Тогда на множестве 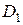определена функция 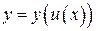, которая называется сложной функцией от (или суперпозицией заданных функций, или функцией от функции).

Переменную 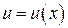называют промежуточным аргументом сложной функции.

Пример. Функция 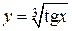есть суперпозиция двух функци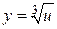й и .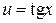

Сложная функция может иметь несколько промежуточных аргументов.

Пример. Функция 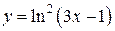является сложной функцией двух промежуточных аргументов 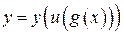, где 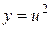, а промежуточные аргументы: 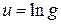и .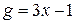

Определение. Функции, составленные из основных элементарных функций, называются элементарными, если удовлетворяют двум условиям: задаются одним аналитическим выражением в области определения; представляют результат конечного числа алгебраических операций и операций взятия функции от функции.

Примеры. Неэлементарнымифункциями могут служить следующие функции:

1. 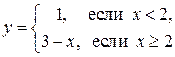– функция в области определения задана двумя аналитическими выражениями.

2. 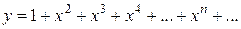– формула, задающая функцию, состоит из бесчисленного числа операций.

Элементарные функции разделяют на два класса: алгебраические и трансцендентные функции.

Определение. Функция называется алгебраической, если её значение можно получить, производя над независимой переменной конечное число алгебраических действий: сложений, вычитаний, делений и возведений в степень с рациональным показателем.

Среди алгебраических функций в свою очередь выделяют:

1. Рациональные функции, если среди алгебраических действий, производимых над независимой переменной, отсутствует операция извлечения корня:

– многочлены 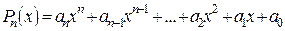, например, .

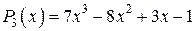– дробно-рациональные функции (отношение многочленов)

,

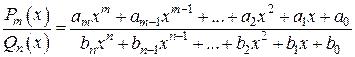например .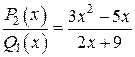

2. Иррациональные функции, если среди алгебраических действий, производимых над независимой переменной, есть операция извлечения корня, например: ; .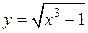

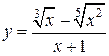Определение. Функции, не являющиеся алгебраическими, называются трансцендентными.

К трансцендентным функциям относятся:

– показательная;

– логарифмическая;

– тригонометрические;

– обратные тригонометрические;

– гиперболические .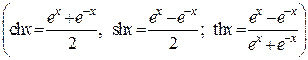

Пример. 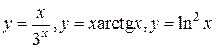– трансцендентные функции.

Понятие предела является одним из основных в математическом анализе. В элементарной математике с помощью предельных переходов определяется длина окружности, объемы цилиндра и конуса, сумма членов бесконечно убывающей геометрической прогрессии.