Вычисление опр-ных интегралов с пом.рядов
Для вычисления определенных интегралов 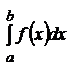
Подинтегральную ф-цию разлагают в ряд Маклорена и в области равномерной сходимости возможно почленное интегрирование
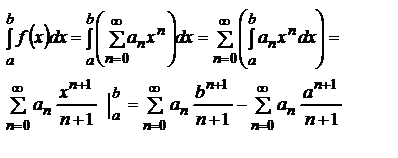
35.1.Интеграл вида ∫R(sin²x¸cos²x)dx
1. Интегралы вида 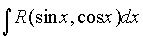 , где , где 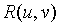 рациональная функция от u и v. рациональная функция от u и v. |
| Интегралы указанного вида сводятся к интегралам от рациональной функции новой переменной t с помощью |
подстановки 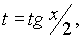 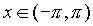 , которую называют универсальной тригонометрической подстановкой. При этом используются формулы тригонометрии , которую называют универсальной тригонометрической подстановкой. При этом используются формулы тригонометрии 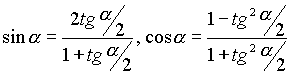 . . |
| Замечание. Универсальная тригонометрическая подстановка часто приводит к громоздким вычислениям. Поэтому чаще применяются другие подстановки. |
2. Подынтегральная функция 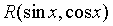 удовлетворяет условию удовлетворяет условию |
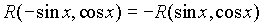 (1) (1) |
| или условию |
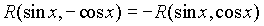 . (2) . (2) |
Тогда можно использовать подстановку 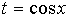 , , 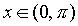 или или 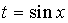 , , 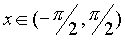 соответственно. соответственно. |
3. Подынтегральная функция 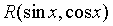 удовлетворяет условию удовлетворяет условию 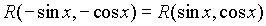 . Это условие выполняется в частности для функций, содержащих только четные степени . Это условие выполняется в частности для функций, содержащих только четные степени 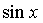 и и 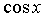 В этом случае часто применяют замену переменной В этом случае часто применяют замену переменной 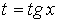 , где , где 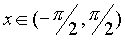 или или 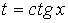 , где , где 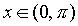 .При этом, так как .При этом, так как 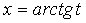 или или 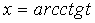 ,то ,то 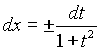 . Функции . Функции 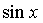 и и 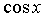 выражаются через t с помощью тригонометрических формул выражаются через t с помощью тригонометрических формул 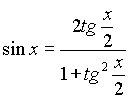 и и 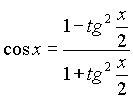 . . |
35.2.Разложение в ряд ф-ции y=arcsinx и y=lg(1+x)
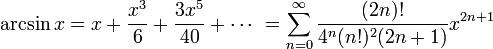 для всех
для всех 
1) 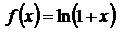 ;
;
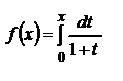 ;
;
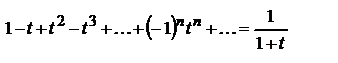 ;
;
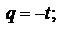
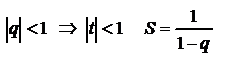
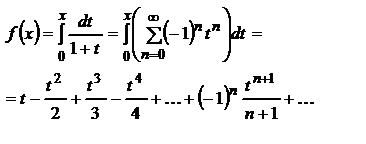
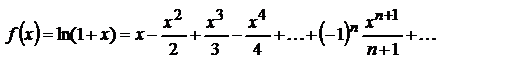
при X=1 ряд тоже сходится 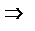
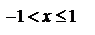
36.1.Интеграл ∫sinmxcosnxdx
4. Вычисление интегралов вида 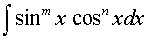 , где m и n ? целые числа. , где m и n ? целые числа. |
| В этом случае полезно пользоваться следующими правилами: |
А) если m - нечетное положительное число, то вносим 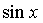 под знак дифференциала или, (что то же самое) делаем замену переменной под знак дифференциала или, (что то же самое) делаем замену переменной 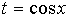 . При этом число n может быть рациональной дробью. Аналогично, если n - нечетное положительное число, то вносим под знак дифференциала . При этом число n может быть рациональной дробью. Аналогично, если n - нечетное положительное число, то вносим под знак дифференциала 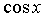 или применяем подстановку или применяем подстановку 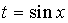 . Сравни с 1. . Сравни с 1. |
Б) если оба показателя m и n - четные положительные числа, то подынтегральную функцию преобразуют с помощью формул понижения степени: 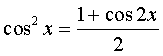 , , 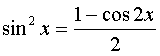 и и 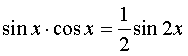 |
В) если число m+n является четным отрицательным числом, то можно сделать замену переменной 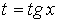 или или 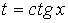 |
| Г) если степени m и n отрицательны, то часто бывает полезным уменьшить степени с помощью основного тригонометрического тождества. |
Примечание. В общем случае интегралы вида 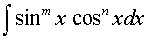 , где m и n - целые числа, вычисляются с помощью рекуррентных формул, которые выводятся путем интегрирования по частям. , где m и n - целые числа, вычисляются с помощью рекуррентных формул, которые выводятся путем интегрирования по частям. |
Биномиальный ряд
степенной ряд вида
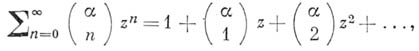
Биномиальный ряд, бесконечный ряд, являющийся обобщением формулы Ньютона бинома (1 + х) n на случай дробных и отрицательных показателей n:
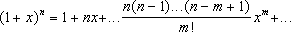
Биномиальный ряд сходится: при —1 < x <1, если n < —1; при —1< x £ 1, если —1 < n < 0; при —1 £ x £ 1, если n > 0.
