Упражнения для самостоятельной работы
1. Для функции 
: 
, 
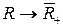найти 
, 
, 
, 
.
2. Для функции : 
, 
найти 
, , 
, 
, построить график.
3. Даны функции : 
, 
, 
: , 
, 
: 
, 
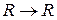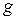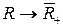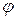. Найти 
, 
, 
, построить график.
4. Какие из данных отображений являются инъекцией, сюръекцией, биекцией:
а) : , 
;
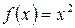б) : 
, 
;
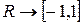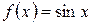в) : 
, 
;
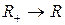г) : 
, 
;
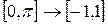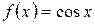д) : , 
;
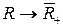е) : 
, .
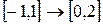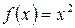5. Пусть : 
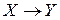и 
, 
. Проверить справедливость следующих соотношений: 
, 
и если 
, то 
.
6. Пусть : 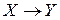и 
, 
. Проверить справедливость следующих соотношений: 
, 
, если , то 
, 
.
7. Даны : , ; : , 
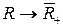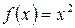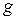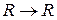. Определить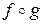 
, 
.
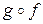8. Для функций : , 
; : , 
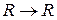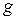определить , .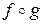
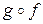9. Для функций : 
, 
; : , 
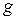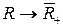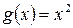, определить , .
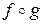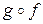10. Для функци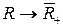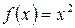й : , и :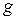
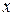 | -1 | ||||
 | -1 |
определить , .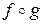
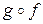11. Проверить, какие из следующих отображений являются обратимыми. Для обратимых функций определить обратные:
а) : 
, 
;
б) 
, 
;
в) :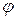 
, 
;
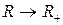г)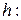 
: , 
;
д) 
:
| | ||||
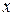 | -1 | -1 |
:
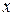| | -1 | |||
 | -1 |
12. Проверить следующее утверждение: есл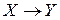и : и :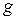 
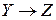- два биективных отображения, то отображение 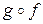также биективно и его обратным отображением будет отображение 
.
13. Для функций : , 
; : , 
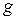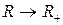определить , .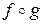
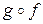14. Заданы числовые функции : , 
; : 
, 
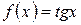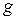. Определить функции 
, 
, 
, 
.
15. Определить , , , , если : , 
; : , .
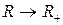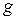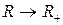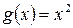Литература
1. Колмоговоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. – М.: Наука, 1976.
2. Канторович Л.В., Акилов Г.П. Функциональный анализ. – М.: Наука, 1977.
3. Ильин В.А., Садовничий В.А., Сендов Б.Х. Математический анализ. – М.: МГУ, 1985.
4. Кудрявцев Л.Д. Математический анализ. Т.1. – М.: Высшая школа, 1973.
5. Шнейдер В.Е., Слуцкий А.И., Шумов А.С. Краткий курс высшей математики. – М.: Высшая школа, 1978.