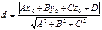Ур-е с угловым коэффициентом

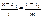
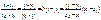
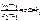
y-y₁=k₁(x-x₁)

y=k₁x-k₁x₁+y₁

y₁-k₁x₁=b

y=k₁x+b

ур-е прямой с угловым коэффициентом k.

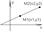Пусть даны 2 точки M₁(x₁,y₁),

M₂(x₂,y₂) и x₁¹x₂, y₁¹y₂.

Для составления Ур-ия

прямой М₁М₂ запишем

уравнения пучка прямых, проходящих

через точку М₁: y-y₁=k(x-x₁). Т.к. М₂лежит на

данной прямой, то чтобы выделить ее из

пучка, подставим координаты точки М₂ в

уравнение пучка

М₁: y-y₁=k(x-x₁) и найдем k:

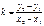
Теперь вид искомой

прямой имеет вид:

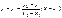
или:

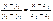
- Ур-е прямой, проходящей ч/з 2

Угол м/ду прямыми на плоскости.

Условия || и^.

а)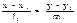

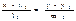
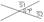
S₁{l₁,m₁} S₂{l₂,m₂},

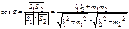
или

p:y=k₁x+b₁, k₁=tgj₁

q:y=k₂x+b₂, k₂=tgj₂ =>tgj=tg(j₂-j₁)=

=(tgj₂-tgj₁)/(1+ tgj₁tgj₂)=

=(k₂-k₁)/(1+k₁k₂).

б) p||q, tgj=0, k₁=k₂

в)p^q,то

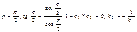
Расстояние от точки до прямой на

Плоскости и до плоскости в пространстве.

1. Ax+By+C=0, M₀(x₀,y₀)

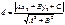
2. Пусть плоскость задана ур-ем Ax+By+Cz+D=0