Работа с матрицами и векторами

Фундаментальным принципом построения системы MATLAB является ее ориентация на операции с массивами. Массив – упорядоченная, пронумерованная совокупность однородных данных. Такими данными могут быть действительные и комплексные числа, переменные либо арифметические выражения. У массива должно быть имя. Массивы различаются по числу размерностей или измерений: одномерные, двумерные, многомерные. Размером массива называют число элементов вдоль каждого из измерений. Под вектором в MATLAB понимается одномерный массив данных, а под матрицей – двумерный или многомерный массив. Если элементы вектора представлены в виде столбца, такой вектор называется вектором-столбцом, а если в виде строки, вектор называется вектором-строкой.

Исходные значения векторов можно задавать с клавиатуры путем поэлементного ввода. Для этого в командной строке следует вначале указать имя вектора, потом поставить знак присваивания =, далее – открывающую квадратную скобку, а за ней ввести заданные значения элементов вектора, отделяя их пробелами или запятыми. Завершается строка закрывающей квадратной скобкой. Так, ввод

V=[1 2 3]

V =

1 2 3

задает вектор-строку V, содержащую три элемента со значениями 1,2,3.

Параллельное использование запятых и пробелов допустимо даже в пределах ввода одного вектора: записи V=[1,2,3] и V=[1 2,3] эквивалентны предыдущей.

Оператор <:> (двоеточие) дает возможность простого создания векторов, каждый элемент которых отличается от предшествующего на постоянную величину, т.е. шаг. Например:

>> V=-0.1:0.3:1.4

V =

-0.1000 0.2000 0.5000 0.8000 1.1000 1.4000

При автоматическом заполнении шаг, равный единице, допускается не указывать. Шаг может быть и отрицательным.

Т.е., если требуется сформировать вектор, элементу которого расположены в арифметической прогрессии то проще всего это сделать так:

x=xn:h:xk

xn – начальное значение;

xk – конечное значение;

h – шаг изменения.

Если шаг не указан, то он равен 1.

Таким образом хорошо задавать, например время изменения сигнала или создавать массив координаты.

Пример формирования вектора с использованием логических операторов

x1=-pi:0.01:pi;

y1=-1.*(x1<=-pi/2) + 0.*(x1>-pi/2 & x1<=pi/2) + 1.*(x1>pi/2);

Возможно задание вектора с помощью оператора linspace.

>> u=linspace(3,20,4)

u =

3.0000 8.6667 14.3333 20.0000

Возможен ввод векторов в виде арифметических выражений, содержащих любые встроенные функции. Например:

>> V=[2+2/(3+4),exp(5),sqrt(10)]

V =

2.2857 148.4132 3.1623

Вектор-столбец A вводится аналогично, но значения элементов в перечне отделяются знаком <;>:

>> A=[1.3;5.4;6.9]

A =

1.3000

5.4000

6.9000

Вектор-столбец можно создать транспонированием вектор-строки (оператор ‘).

Можно производить и составления матрицы путем объединения матриц или векторов между собой (здесь вектора A1 A2 были определены заранее):

>> Q=[A1;A2];

При этом вектор A1 будет формировать первую строку матрицы, а вектор A2 вторую.

Знак <;> также используется для разделения строк при задании матриц. Один из способов ввода матрицы основан на том, что матрицу можно рассматривать как вектор-столбец, каждый элемент которого является строкой матрицы. Поскольку точка с запятой используется для разделения элементов вектор-столбца, то комбинируя оба варианта разделителей, можно сформировать матрицу

B=.

>> B=[1 3 0;-2 -2 5]

B =

1 3 0

-2 -2 5

Матрицы небольших размеров удобно вводить из командной строки. Вначале ставится открывающая квадратная скобка. Затем элементы каждой строки матрицы набираются через пробел, а ввод строки завершается нажатием на клавишу <Enter>. При вводе последней строки в конце ставится закрывающая квадратная скобка. Если после закрывающей квадратной скобки не ставить точку с запятой для подавления вывода в командное окно, то матрица выведется в виде таблицы.

Так можно сформировать предыдущую матрицу B:

>> B=[1 3 0

-2 -2 5]

B =

1 3 0

-2 -2 5

Доступ к элементам вектора осуществляется при помощи индекса (целое положительное число), заключаемого в круглые скобки после имени массива, в котором хранится вектор. Если введен массив V, определенный вектор-строкой

>> V=[3.1 4.5 7.1 2.2 0.8];

то для вывода, например, его третьего элемента, используется индексация:

>> V(3)

ans =

7.1000

Если нужно, наоборот, вставить на это место некоторое число, например π, то это можно сделать так:

>> V(3)=pi

v =

3.1000 4.5000 3.1416 2.2000 0.8000

Возможно использование служебного слов end.

>> vx=V(end)

vx =

0.8000

Доступ к элементам матриц осуществляется при помощи двух индексов – номеров строки и столбца, заключенных в круглые скобки и расположенных после имени, в котором хранится массив данных, например:

>> M=[1 2 3 4;5 6 7 8];

>> M(2,3)

ans =

Если в приведенной матрице на место элемента, обозначенного цифрой 7, нужно вставить другое число, например e, то это можно сделать так:

>> M(2,3)=exp(1)

M =

1.0000 2.0000 3.0000 4.0000

5.0000 6.0000 2.7183 8.0000

Обратите внимание на то, что после операции присваивания нового значения хотя бы одному элементу матрицы, не завершенной точкой с запятой, матрица М целиком выводится в командное окно.

Присвоить можно и значение элементу матрицы, индексы которого превышают текущие ее размеры. В этом случае эти размеры будут соответственно увеличены, а остальные элементы такой расширенной матрицы будут заполнены нулями:

>> A=[1 2]

A =

1 2

>> A(2,3)=5

A =

1 2 0

0 0 5

Элементы массивов могут входить в состав выражений.

>> A(1,1)/A(1,2)-A(2,3)

ans =

-4.5000

Если необходимо произвести обращение не к одному элементу, а к нескольким или, точнее, выделить из общей матрицы подматрицу, то поступают так A(1:5,6:8), при этом произошло выделение подматрицы начиная с 1 строки и кончая 5 и выделили столбцы с 6 по 8. Если необходимо выделить весь столбец (строку), то вместо указания конкретных номеров можно просто поставить пустое двоеточие (A(:,6:8)).

>> A=magic(8)

A =

64 2 3 61 60 6 7 57

9 55 54 12 13 51 50 16

17 47 46 20 21 43 42 24

40 26 27 37 36 30 31 33

32 34 35 29 28 38 39 25

41 23 22 44 45 19 18 48

49 15 14 52 53 11 10 56

8 58 59 5 4 62 63 1

>> A(:,6:8)

ans =

6 7 57

51 50 16

43 42 24

30 31 33

38 39 25

19 18 48

11 10 56

62 63 1

Возможности знака оператора <:> (двоеточие):

j:k эквивалентно [j, j+1, ..., k]

j:k пустое множество, если j > k, т.е. []

j:i:k эквивалентно [j, j+i, j+2i, ..., k]

j:i:k пустое множество, если i > 0 и j > k или, если i < 0 и j < k, где i, j и k - скаляры.

Примеры использования двоеточия при работе с векторами, матрицами и многомерными массивами:

A(:, j) – j-й столбец A

A(i, :) – i-й ряд A

A(:, :) – это эквивалентный двумерный массив. Для матрицы данная запись эквивалентна A.

A(j: k) – это A(j), A(j+1), ..., A(k)

A(:, j:k) – это A(:, j), A(:, j+1), ..., A(:, k)

A(:, :, k) – это k-я страница трехмерного массива A.

A(i, j, k, :) – это вектор в четырехмерном массиве A. Компоненты вектора: A(i, j, k, 1), A(i, j, k, 2), A(i, j, k, 3), и т.д.

A(:) – это все элементы A, представленные в виде вектора-столбца.

Перечень элементарных функций для работы с матрицами можно получить командой doc elmat.

Функция size(B) позволяет узнать размер массива B, она возвращает результат в виде вектора, первый элемент которого равен числу строк, а второй – столбцов:

>> B=[1 2 3;4 5 6];V=[1 2 3];A=[1;2;3];a=5;

>> disp(size(B))

2 3

>> disp(size(V))

1 3

>> disp(size(A))

3 1

>> disp(size(a))

1 1

Итак, B, V, A ,a – массивы размеров 2×3, 1×3, 3×1, 1×1 соответственно.

Результатом применения функции length(V) к вектору V является длина вектора, т.е. число его элементов:

>> disp(length(V))

Функция ndims(B) отображает размерность массива B.

>> disp(ndims(B))

>> disp(ndims(a))

>> disp(ndims(V))

Итак, B, a, V – массивы размерности 2 установленных выше размеров.

В MATLAB можно создавать массивы размерности и выше 2.

Пример:

>> p(1,1,2)=1

p(:,:,1) =

p(:,:,2) =

>> disp(size(p))

1 1 2

>> disp(ndims(p))

Итак, введен массив p размерности 3 размера 1×1×2 с двумя элементами p(1,1,1) =0 и p(1,1,2) =1.

Можно вывести значение любой переменной a в командное окно, для чего следует набрать имя переменной в командной строке и нажать <Enter>, либо вызвать функцию disp(a).

Просмотр текущих переменных рабочей среды производится при помощи команды whos. Предположим, что ранее переменным a , b и с были присвоены значения:

>> a= -1.34;

>> b=2.98+3.86i;

c=[1 2 3;-5 6 -1]

c =

1 2 3

-5 6 -1

Вызовем команду whos, указав через пробелы имена переменных

>> whos a b c

В командное окно выводится таблица, приведенная ниже.

Name Size Bytes Class

a 1x1 8 double array

b 1x1 16 double array (complex)

c 2x3 48 double array

В столбике Class указан тип переменной, в Bytes – число байт, выделенных под хранение значения, а столбик Size содержит информацию о размере переменных. После таблицы размещена строка с указанием суммарного объема памяти в байтах.

MATLAB запоминает значения всех переменных, определенных во время сеанса работы, даже если применена команда очистки экрана clc.

После ввода этой команды экран будет очищен. Для того, чтобы узнать, какие переменные уже использованы, а какие нет, служит команда who, выводящая в комадное окно список используемых переменных:

>> who

Your variables are:

a b c

Для удаления из памяти всех переменных используется команда clear. Если за ней указать список переменных (через пробел), то только они будут удалены из памяти, например:

>> clear b

>> who

Your variables are:

a c

Окно Workspace содержит таблицу, аналогичную той, что выводится командой whos.

Двойной щелчок левой кнопкой мыши на строке с именем переменной в окне Workspace отображает в отдельном окне редактора переменных Variablesее матричное представление. На рис. 2.11 показано отображение переменной c.

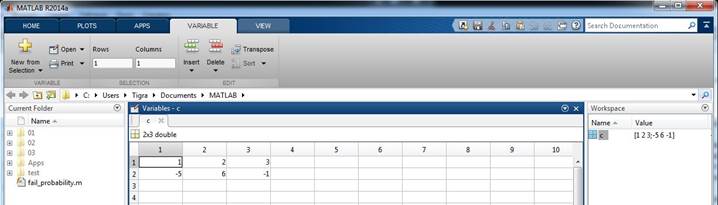
Рис. 2.11

В окне Variablesи в верхней линейке меню в соответствующих полях задается активная позиция в матрице, и далее вводятся числа, выражения, переменные и функции в отдельные клетки таблицы. Этот способ обеспечивает быстрый доступ к элементам матрицы и позволяет их вводить или редактировать в произвольном порядке.

При щелчке правой кнопкой мыши на строке с именем переменной в окне Workspace появляется всплывающий список команд. Команды списка позволяют переименовать переменные, удалить лишние, сохранить рабочую среду и т.д. Так, щелчок на строке с именем команды Open selection(Открыть выделение) приводит к отображению этой переменной в окне Variables.

Один из способов формирования векторных и матричных массивов состоит в создании пустого массива

>> M=[]

M =

[]

размера 0×0, который затем заполняется с использованием редактора переменных Variables.

MATLAB позволяет выполнять мощные групповые вычисления над массивами, используя обычные математические функции, которые в традиционных языках программирования работают только со скалярными аргументами. Групповые операции позволяют компактно задавать выражения, при которых выполняется гигантский объем работы. Кроме того, матричные вычисления выполняются намного быстрее, чем скалярные.

К матричным действиям с матрицами относятся такие операции, которые используются в матричном исчислении в математике.

Базовые действия с матрицами (векторами) – сложение, вычитание, транспонирование, умножение матрицы на число, умножение матрицы на матрицу, возведение квадратной матрицы в степень – осуществляются в MATLAB с помощью обычных знаков арифметических операций. Условия, при которых эти операции возможны, таковы:

- при сложении или вычитании матриц они должны иметь одинаковые размеры;

- при умножении матриц число столбцов первого множителя должно совпадать с числом строк второго множителя.

Невыполнение этих условий приводит к появлению сообщения об ошибке.

Приведем несколько примеров действий с матрицами

А = , D = , B = .

>> A=[0 -2 4;3 2 1];D=[-5 4 2;1 3 1];B=[-1 -2 -3;1 3 1;0 2 2];

Пример сложения и вычитания

>> disp(A+D)

-5 2 6

4 5 2

>> disp(D-A)

-5 6 -2

-2 1 0

Пример умножения на число

>> disp(3*D)

-15 12 6

3 9 3

Пример транспонирования матрицы, при котором ее строки становятся столбцами с теми же номерами, а столбцы – строками, осуществляется с помощью оператора апостроф <'>:

>> disp(A')

0 3

-2 2

4 1

В математике транспонированная матрица А обозначается А^Т.

Знак <*> закреплен за матричным умножением векторов и матриц в смысле линейной алгебры. При этом число столбцов первой матрицы обязано равняться числу строк второй матрицы. Произведение прямоугольной матрицы A_n×k (таблицы чисел, расположенных в n строках и в k столбцах) на матрицу B_k×m определяется следующим образом: для того, чтобы получить элемент c_ij матрицы - произведения C=AB, следует элементы i -й строки матрицы А умножить на соответствующие элементы j -го столбца матрицы В и результаты сложить, т. е.

c_ij = .

Матрица С = С_n×m занимает n строк и m столбцов.

Пример умножения матрицы на матрицу

>> C=A*B

C =

-2 2 6

-1 2 -5

Умножение двух векторов определено в математике только для векторов одинакового размера и лишь тогда, когда один из векторов сомножителей

является строкой, а второй – столбцом. Иначе говоря, если векторы Х и У являются строками, то математический смысл имеют только две формы умножения этих векторов: U=X*Y' и V=X'*Y. Причем в первом случае результатом будет скалярное произведение векторов Х и Y (число), а во втором – внешнее произведение векторов Х и Y (квадратная матрица). Пример:

>> x=[1 2 3];y=[4 5 6];

>> v=x*y'

v =

>> v=x'*y

v =

4 5 6

8 10 12

12 15 18

Скалярное произведение двух векторов возвращает функция dot.

>> s=dot(x,y)

s =

Векторное произведение. Для трехкомпонентных векторов в MATLAB существует функция cross, которая позволяет найти векторное произведение двух векторов. Пример:

>> v1=[1 2 3];v2=[4 5 6];

>> cross(v1,v2)

ans =

-3 6 -3

Функцияdet(B) – вычисляет определитель│B│ квадратной матрицы B.

>> d=det(B)

d =

-6

Функция обращения матрицы – inv(B) – вычисляет матрицу, обратную заданной матрице B. Исходная матрица B должна быть квадратной, и ее определитель не должен быть равен нулю.

Пример:

>> B1=inv(B)

B1 =

-0.6667 0.3333 -1.1667

0.3333 0.3333 0.3333

-0.3333 -0.3333 0.1667

Матрица, обратная матрице В, обозначается В^-1 и удовлетворяет соотношениям (В^-1)^-1 = B, ВВ^-1 = В^-1В = E, где E – единичная матрица того же порядка n, что и B.

Проверим правильность результата выполнения операции обращения матрицы B:

>> disp(inv(B1))

-1.0000 -2.0000 -3.0000

1.0000 3.0000 1.0000

0 2.0000 2.0000

В результате получили матрицу B, т.е. соотношение (В^-1)^-1 = B выполняется.

>> disp(B*B1)

1.0000 0 0

-0.0000 1.0000 -0.0000

0 0 1.0000

>> disp(B1*B)

1.0000 0 0

0 1.0000 0

0 -0.0000 1.0000

В результате получили единичную матрицу Е, т.е. соотношения ВВ^-1 = В^-1В = E также выполняются.

Примеры возведения квадратной матрицы в степень

>> disp(B^2)

-1 -10 -5

2 9 2

2 10 6

>> disp(B^-1)

-0.6667 0.3333 -1.1667

0.3333 0.3333 0.3333

-0.3333 -0.3333 0.1667

При возведении матрицы в целую положительную степень происходит матричное умножение матрицы на саму себя столько раз, каков показатель степени, в отличие от поэлементного возведения матрицы в степень при помощи оператора <.^>. Для отрицательных степеней вычисляется степень обратной матрицы.

Возможно использование дробных степеней. Извлечем из матрицы B кубический корень D=.

>> D=B^(1/3)

D =

0.5355 + 0.7217i -0.3647 - 0.0000i -0.7244 + 0.7217i

0.2356 - 0.2165i 1.4422 0.2356 - 0.2165i

-0.0355 + 0.1443i 0.3647 1.2244 + 0.1443i

Проверим результат возведением в куб.

>> D^3

ans =

-1.0000 + 0.0000i -2.0000 - 0.0000i -3.0000 + 0.0000i

1.0000 - 0.0000i 3.0000 - 0.0000i 1.0000 - 0.0000i

0.0000 + 0.0000i 2.0000 + 0.0000i 2.0000 - 0.0000i

>> real(ans)

ans =

-1.0000 -2.0000 -3.0000

1.0000 3.0000 1.0000

0.0000 2.0000 2.0000

Соотношение D³= B выполняется, т.е. кубический корень D= найден верно.

Если требуется извлечь квадратный корень из матрицы, то лучше применить встроенную функцию sqrtm. Матричные экспонента и логарифм вычисляются при помощи функций expm и logm.

В MATLABвводятся две новые функции (они не относятся к традиционным математическим операциям над векторами и матрицами) деления матриц слева направо и справа налево. Первая операция записывается при помощи знака < / >, а вторая – при помощи знака < \ >, которые помещаются между именами матриц – делимого и делителя. Операция B/A эквивалентна операции B*inv(A) и ее удобно использовать для решения матричного уравнения

X*A=B,

а A\B эквивалентна inv(A)*B и является решением матричного уравнения

A*X=B.

Таблица 2 Функции матричных действий
Функция и ее синтаксис	Описание
zeros(m, n)	Возвращает нулевую матрицу (состоящую из одних нулей) размерности mхn.
ones(m, n)	Возвращает матрицу состоящую из одних единиц размерности mхn.
eye(m, n)	Создает единичную матрицу размерности mхn.
rand(m, n)	Возвращает матрицу случайных чисел равномерно распределенных в диапазоне от 0 до 1, матрица имеет размерность mхn.
randn(m, n)	Возвращает матрицу размерности mхn, состоящих из случайных чисел в диапазоне от 0 до 1 и имеющих Гаусовское распределение (имеющих нормальный закон распределения).
reshape(A, n, m)	Функция образует матрицу размерности nхm путем выборки элементов заданной матрицы А по столбцам и последующему распределению этих элементов по m столбцам каждый из которых содержит n элементов, при этом матрица А должна иметь размерность nхm.
tril(A)	Выбирает нижнюю треугольную матрицу из матрицы А
triu(A)	Выбирает верхнюю треугольную матрицу из матрицы А
diag(A, n)	Функция создает диагональную матрицу из вектора А, при этом второй параметр необязателен. Если второй параметр присутствует, то создается матрица в которой вектор А помещается в другую диагональ, при этом если n>0, то вектор помещается выше главной диагонали, если n <0 то ниже, если n=0 то на главную диагональ. Если А матрица, то функция выдает вектор сформированный из элементов главной ее диагонали, если второй параметр отсутствует или равен нулю. Если второй параметр присутствует, то функция выдает другую диагональ, в соответствие с вторым параметром (см. предыдущий абзац).
’ (апостроф)	Оператор производит транспонирование матрицы
+ - * / \ ^	Математические действия над матрицами. Применимы как к выражению вида «матрица-скаляр», так и «матрица-матрица» (за исключением возведения в степень, он применима только к выражению «матрица-скаляр»). Во всех операциях необходимо следить за размерностями матриц.
inv(A)	Возвращает обратную матрицу по отношению к матрице А
det(A)	Подсчет определителя (детерминанта) матрицы
cross(A, B)	Векторное произведение векторов
.* ./ .\ .^	Поэлементные операции. При применении этих операций матрицы должны иметь одинаковые размерности, или же быть скалярами (числом). Пи этом происходит сопоставление элементов одной матрицы элементам другой матрицы и выполняется соответствующая операция.
size(A)	Возвращает максимум состоящий из числа строк (первый элемент) и числа столбцов (второй элемент).
sum(A)	Возвращает сумму всех элементов по столбцу
mean(A)	Возвращает среднее значение столбца матрицы
std(A)	Возвращает среднеквадратическое отклонение столбца матрицы
min(A) max(A)	Возвращает минимум и максимум соответственно, по столбцу матрицы
sort(A)	Сортирует столбец матрицы по возрастанию
prod(A)	Вычисляет произведение всех элементов столбцов

Многомерные матрицы

Многомерная матрица – матрица имеющая размерность большую двух. Если обычную матрицу мы представляли как двумерное пространство (если вектор, то прямая), то многомерная матрица представляет из себя n-мерное пространство.