И попересной силы q

При выполнения, расчетно-проектировочной работы ограничиваемся рассмотрением статически определимых стержней. Попереч­ная нагрузка представляет собой в общем случае сосредоточен­ную силу Р и распределенную по части длины стержня нагрузку q, координаты точек приложения которых задаются.

Эпюры М и Q в статически определимых балках строятся с помощью известных способов [2], [3].

В качестве примера рассмотрим построение эпюр М и Q для стержня, изображенного на рис.4.

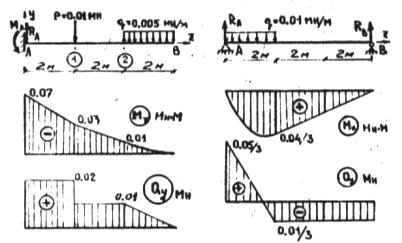
Рис.4 Рис.5

Определяем реактивные усилия М_А, R_A в заделке – точке А. Для этого составляем уравнения статического равновесия

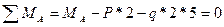
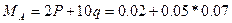МН М

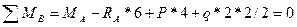
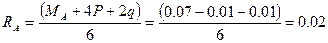МН.

Проверка выполняется, поэтому величины реактивных усилий найдены правильно.

.

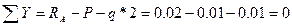Условие выполняется, поэтому величины момента M(Z) и поперечной силы Q(Z) для соответствующих участков балки.

Участок А – 1: 0≤Z≤2 М.

М(Z)= -M_A+R_AZ= -0.07+0.02

Q(Z)= R_A=0.02 МН

При Z=0: M(0)=-0.07 МН М

Z=2 M: M(2)=-0.07+0.02 2=-0.03 МН M

Участок 1 – 2: 2М≤Z≤4M

M(Z)= -M_A+R_AZ-P(Z-2)= -0.07+0.02*Z-0.01(Z-2)

Q(Z)= R_A-P= 0.01 MH

При Z= 2M: M(2)= -0.03 MH M

Z= 4M: M(4)= -0.07+0.02*4-0.01*2= -0.01 MH M

Участок 2 – В: 0≤Z≤2 M, ось Z, направлена противоположно оси Z и начинается на правом конце балки.

M(Z)= -qZ₁²/2= -0.005 Z₁²/2

Q(Z)= qZ₁= 0.005*Z

При Z= 0: M(0)= 0, Q(0)= 0

Z=2M: M(2)= -0.01 MH M, Q(2)= 0.01 MH.

Вид эпюр M(Z) и Q(Z) приведен на рис. 4. При построении эпюр изгибаемого момента M(Z) и поперечной силы Q(Z) реко­мендуется использовать следующие зависимости:

- на участках балки, где поперечная нагрузка q=const, перерезывающая сила Q(Z=0), а изгибающиймомент М (Z) меняется по линейному закону;

- на участках балки, где q=const перерезывающая (попе­речная) сила Q(Z) меняется по линейному закону, а M(Z) по вагону квадратичной параболы.

Для закрепления материала, относящегося к определении ве­личин реактивных усилий и построению эпюр M(Z) и Q(Z), реко­мендуется проделать необходимые выкладки и построить эпюры для стержня, приведенного на рис.5. Полученные результаты надо сравнить с данными рис.5.

При дальнейшем изложении материала вместо величины изгибающего момента вводим в рассмотрение величину приведенного момента 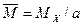, которая используется при определении величины нормального напряжения σ.