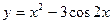Дифференциальное исчисление функций одной переменной
Линейная алгебра
$$$ 1
Вычислить 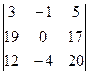
$$$ 2
Вычислить 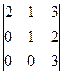
$$$ 3
Вычислить 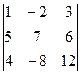
$$$ 4
Решить уравнения: 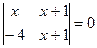
$$$ 5
Решить уравнения: 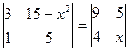
$$$ 6
Решить уравнения: 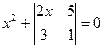
$$$ 7
Найти алгебраическое дополнение 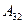 определителя
определителя 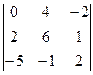
$$$ 8
Найти алгебраическое дополнение 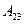 определителя
определителя 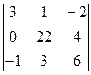
$$$ 9
Найти матрицу 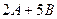 , если
, если 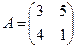 и
и 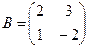
$$$ 10
Найти матрицу 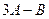 , если
, если 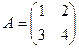 и
и 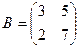
$$$ 11
Найти 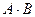 , если
, если 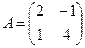 и
и 
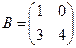
$$$ 12
Найти 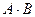 , если
, если 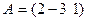 и
и 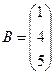
$$$ 13
Найти 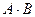 , если
, если 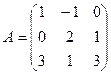 и
и 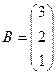
$$$ 14
Решить систему уравнений 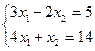 найти
найти 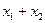
$$$ 15
Решить систему уравнений 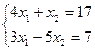 найти
найти 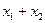
$$$ 16
Решить систему уравнений 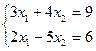 и найти
и найти 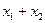
$$$ 17
Решить систему уравнений 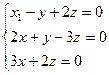
$$$ 18
Для матрицы 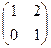 обратной является
обратной является
$$$ 19
Для матрицы 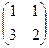 обратной является:
обратной является:
$$$ 20
Дано 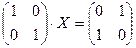 . Найти матрицу X
. Найти матрицу X
$$$ 21
Решить уравнение 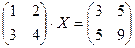
$$$ 22
Определитель третьего порядка 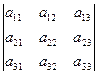 равен:
равен:
$$$ 23
При перестановке двух строк определитель:
$$$ 24
При умножении какой-либо строки определителя на число 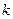 значение определителя:
значение определителя:
$$$ 25
Если элементы одного столбца определителя соответственно равны элементам другого столбца, то определитель
$$$ 26
При разложении определителя 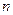 -го порядка по элементам
-го порядка по элементам 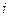 - ой строки его значение равно:
- ой строки его значение равно:
$$$ 27
При разложении определителя 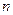 - го порядка по элементам
- го порядка по элементам 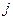 -того столбца его значение равно:
-того столбца его значение равно:
$$$ 28
Алгебраическое дополнение элемента 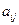 равно:
равно:
$$$ 29
При умножении матрицы 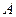 на число
на число 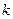 :
:
$$$ 30
Условие, при котором возможна операция умножения матрицы 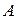 размерности
размерности 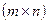 на матрицу
на матрицу 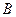 размерности
размерности 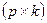 :
:
$$$ 31
Если квадратная матрица 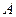 имеет обратную, матрицу
имеет обратную, матрицу 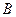 то:
то:
$$$ 32
Если определитель матрицы 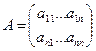 не равен нулю, то
не равен нулю, то 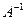 обратная к
обратная к 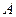 вычисляется по формуле
вычисляется по формуле
$$$ 33
Если определитель квадратной матрицы не равен нулю, то матрица называется:
$$$ 34
Квадратная матрица называется единичной, если у нее
$$$ 35
Минором 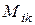 элемента
элемента 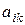 определителя
определителя 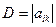 называется:
называется:
$$$ 36
Матрицы 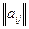 размерности
размерности 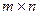 и
и 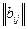 размерности
размерности 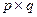 называются равными, если
называются равными, если
$$$ 37
Суммой матриц одинаковой размерности 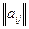 и
и 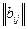 называется матрица
называется матрица 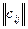 , элементы которой определяются по формуле
, элементы которой определяются по формуле
$$$ 38
Если определитель системы 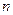 линейных однородных уравнений с
линейных однородных уравнений с 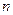 неизвестными не равен нулю, то система
неизвестными не равен нулю, то система
$$$ 39
Система линейных уравнений называется совместной, если она
$$$ 40
Система линейных уравнений называется несовместной, если она
$$$ 41
Для того чтобы система 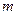 линейных уравнений с
линейных уравнений с 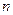 неизвестными была совместной, необходимо и достаточно, чтобы
неизвестными была совместной, необходимо и достаточно, чтобы
$$$ 42
Формулы Крамера для решения системы 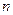 - уравнений с n – неизвестными имеют вид:
- уравнений с n – неизвестными имеют вид:
$$$ 43
Если 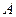 – основная матрица системы линейных уравнений невырожденная, а
– основная матрица системы линейных уравнений невырожденная, а 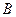 – матрица-столбец свободных членов, то решение системы
– матрица-столбец свободных членов, то решение системы 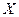 – матрица-столбец неизвестных находится по формуле
– матрица-столбец неизвестных находится по формуле
Векторное алгебра
$$$ 44
Векторы называются равными, если
$$$ 45
Сумма 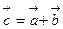 при
при 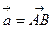 и
и 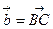 равна
равна
$$$ 46
Векторы 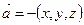 и
и 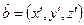 коллинеарны если
коллинеарны если
$$$ 47
Если векторы 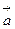 и
и 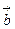 коллинеарны, то найдется число
коллинеарны, то найдется число 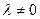 , удовлетворяющее равенству
, удовлетворяющее равенству
$$$ 48
Если векторы 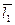 и
и 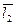 образуют на плоскости базис, то на этой плоскости любой вектор
образуют на плоскости базис, то на этой плоскости любой вектор 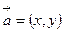 можно единственным образом разложить по данному базису
можно единственным образом разложить по данному базису
$$$ 49
Векторное произведение векторов 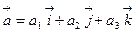 и
и 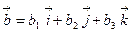
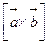 равно:
равно:
$$$ 50
Проекция вектора 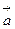 на направленную прямую
на направленную прямую 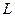 равна
равна
$$$ 51
Скалярным произведением векторов 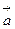 и
и 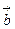 называется число
называется число
$$$ 52
Скалярное произведение векторов 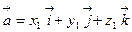 и
и 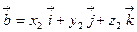 равно
равно
$$$ 53
Векторы 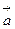 и
и 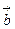 ортогональны, если
ортогональны, если
$$$ 54
Указать необходимое и достаточное условие коллинеарности векторов 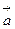 и
и 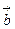
$$$ 55
Смешанное произведение векторов 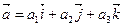 ,
, 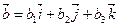 ,
, 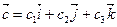 .
. 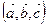 равно
равно
$$$ 56
Указать необходимое и достаточное условия компланарности векторов 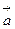 ,
, 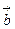 ,
, 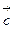
$$$ 57
Векторным произведением векторов 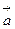 и
и 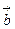 называется вектор
называется вектор 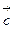 , который удовлетворяет следующим трем условиям:
, который удовлетворяет следующим трем условиям:
$$$ 58
Работа произведенная постоянной силой 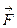 при перемещении тела на пути
при перемещении тела на пути 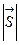 , определяемом вектором
, определяемом вектором 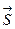 вычисляется по формуле:
вычисляется по формуле:
$$$ 59
Укажите условие ортогональности векторов 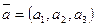 и
и 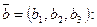
$$$ 60
Три упородоченных вектора 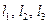 в пространстве образуют базис, если они
в пространстве образуют базис, если они
$$$ 61
Площадь параллелограмма, построенного на векторах 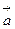 и
и 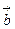 , имеющих общее начало равна
, имеющих общее начало равна
$$$ 62
Найти скалярное произведение векторов 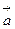 ,
, 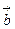 , если
, если 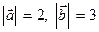
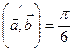
$$$ 63
Найти 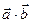 , если
, если 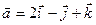 ,
, 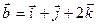
$$$ 64
Найти длину вектора 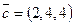
$$$ 65
Найти направляющие косинусы вектора 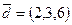
$$$ 66
Найти координаты вектора 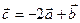 , если
, если 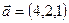 ,
, 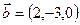
$$$ 67
При каком значении 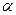 вектора
вектора 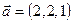 и
и 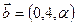 ортогональны
ортогональны
$$$ 68
Найти проекцию вектора 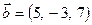 на вектор
на вектор 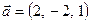
$$$ 69
Найти 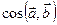 , если
, если 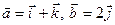
$$$ 70
Найти 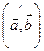 , если для векторов выполняется
, если для векторов выполняется 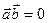
$$$ 71
Найти векторное произведение векторов 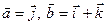
$$$ 72
Найти векторное произведение коллинеарных векторов 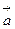 и
и 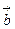
$$$ 73
Найти площадь параллелограмма, построенного на векторах 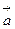 и
и 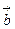 , если
, если 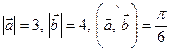
$$$ 74
Найти 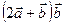 , если
, если 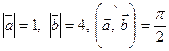
$$$ 75
Найти 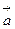
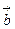
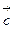 , если
, если 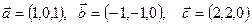
$$$ 76
Найти объем параллелепипеда построенного на векторах 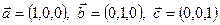
$$$ 77
Найти 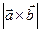 , если векторы
, если векторы 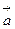 и
и 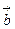 ортогональны и
ортогональны и 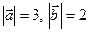
$$$ 78
При каких 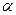 и
и 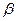 векторы
векторы 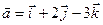 и
и 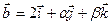 коллинеарны
коллинеарны
$$$ 79
Найти длину вектора 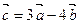 , если
, если 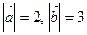 ,
, 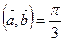
$$$ 80
Чему равен 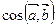 ?
?
$$$ 81
Чему равна проекция вектора 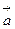 на вектор
на вектор 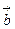 ?
?
$$$ 82
Указать необходимое и достаточное условие коллинеарности векторов 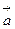 ,
, 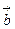
$$$ 83
При каком значении 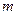 вектора
вектора 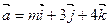 и
и 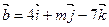 перпендикулярны
перпендикулярны
$$$ 84
Найти 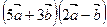 , если
, если 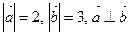
$$$ 85
Найти единичный вектор того же направления, что и вектор 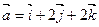
$$$ 86
При каком значении 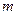 векторы
векторы 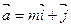 и
и 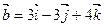 ортогональны
ортогональны
$$$ 87
Найти работу силы 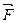 при перемещении тела на пути
при перемещении тела на пути 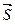 , если
, если 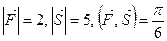
$$$ 88
При каком значении 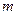 векторы
векторы 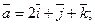
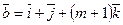 и
и 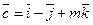 компланарны?
компланарны?
$$$ 89
Найти смешанное произведение векторов 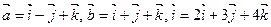
$$$ 90
Найти 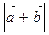 , если
, если 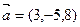 ,
, 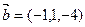
$$$ 91
Найти 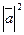 если
если 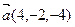
$$$ 92
Найти 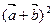 , если
, если 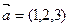 ,
, 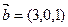
$$$ 93
Найти 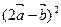 , если
, если 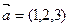 ,
, 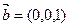
$$$ 94
Найти координаты вектора 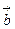 , коллинеарного вектору
, коллинеарного вектору 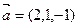 при условии
при условии 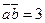
Аналитическая геометрия
$$$ 95
Расстояние между точками 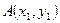 и
и 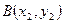
$$$ 96
Даны точки 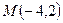 и
и 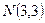 . Найти расстояние между ними
. Найти расстояние между ними
$$$ 97
Дан треугольник с вершинами 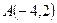 ,
, 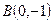 и
и 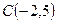 . Найти его периметр
. Найти его периметр
$$$ 98
Даны точки 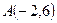 и
и 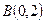 . Найти координаты точки
. Найти координаты точки 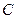 середины отрезка
середины отрезка 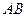
$$$ 99
Определить середины сторон треугольника 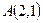 ,
, 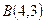 , и
, и 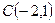
$$$ 100
Уравнение окружности с центром в точке 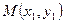 с радиусом 2
с радиусом 2
$$$ 101
Написать уравнение прямой 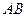 если
если 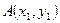 ,
, 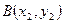
$$$ 102
Общее уравнение прямой на плоскости
$$$ 103
Найти угловой коэффициент 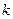 прямой
прямой 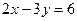
$$$ 104
Дано общее уравнение прямой 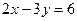 . Написать уравнение прямой в отрезках
. Написать уравнение прямой в отрезках
$$$ 105
Угол между прямыми 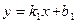
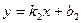
$$$ 106
Условие параллельности прямых 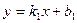 и
и 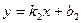
$$$ 107
Условие параллельности прямых 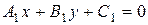
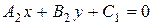
$$$ 108
Условие перпендикулярности прямых 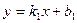 и
и 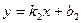
$$$ 109
Уравнение прямой, проходящей через точку 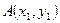 с угловым коэффициентом
с угловым коэффициентом 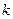
$$$ 110
Найти расстояние от точки 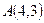 до прямой
до прямой 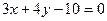
$$$ 111
Найти расстояние от точки 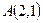 до прямой
до прямой 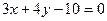
$$$ 112
Дан эллипс 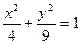 . Найти его полуоси
. Найти его полуоси
$$$ 113
Дана гипербола 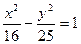 . Найти действительную полуось
. Найти действительную полуось
$$$ 114
Дана гипербола 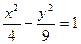 . Найти мнимую полуось
. Найти мнимую полуось
$$$ 115
Дан эллипс 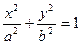 , причем
, причем 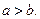 Найти координаты фокусы эллипса
Найти координаты фокусы эллипса
$$$ 116
Дан эллипс 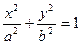 , причем
, причем 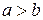 . Найти эксцентриситет эллипса
. Найти эксцентриситет эллипса
$$$ 117
Написать каноническое уравнение эллипса, зная, что расстояние между фокусами равно 8, а малая полуось 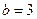
$$$ 118
Написать каноническое уравнение эллипса, зная, что большая полуось 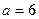 , а эксцентриситет
, а эксцентриситет 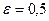
$$$ 119
Найти малую полуось 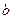 и эксцентриситет эллипса, имеющего большую полуось
и эксцентриситет эллипса, имеющего большую полуось 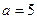 и параметр
и параметр 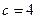
$$$ 120
Найти большую полуось 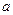 и эксцентриситет эллипса, имеющего малую полуось
и эксцентриситет эллипса, имеющего малую полуось 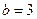 и параметр
и параметр 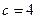
$$$ 121
Чему равно расстояние от центра гиперболы до фокуса
$$$ 122
Дана гипербола 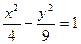 . Чему равна действительная полуось
. Чему равна действительная полуось
$$$ 123
Дана гипербола 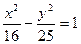 . Чему равна мнимая полуось
. Чему равна мнимая полуось
$$$ 124
Дана гипербола 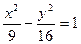 . Найти эксцентриситет
. Найти эксцентриситет
$$$ 125
Дана гипербола 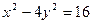 . Найти координаты правого фокуса
. Найти координаты правого фокуса
$$$ 126
Написать каноническое уравнение гиперболы, зная, что расстояния одной из ее вершин от фокусов равны 9 и 1
$$$ 127
Найти координату вершины параболы 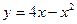
$$$ 128
Найти координату вершины параболы 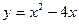
$$$ 129
Даны прямые 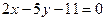 и
и 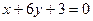 . Найти координаты точки пересечения этих прямых
. Найти координаты точки пересечения этих прямых
$$$ 130
Даны прямые 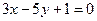 и
и 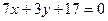 . Найти координаты точки пересечения этих прямых
. Найти координаты точки пересечения этих прямых
$$$ 131
Определить вид линии второго порядка 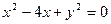
$$$ 132
Определить вид линии второго порядка 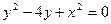
$$$ 133
Дана окружность 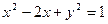 . Найти координаты центра и радиус
. Найти координаты центра и радиус
$$$ 134
Дано общее уравнение плоскости 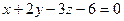 . Уравнение плоскости в отрезках имеет вид
. Уравнение плоскости в отрезках имеет вид
$$$ 135
Даны плоскости 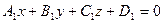 и
и 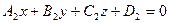 . Эти плоскости параллельны если
. Эти плоскости параллельны если
$$$ 136
Даны плоскости 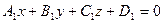 ,
, 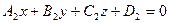 . Эти плоскости взаимно перпендикулярны, если
. Эти плоскости взаимно перпендикулярны, если
$$$ 137
Найти угол между плоскостями 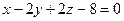
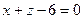
$$$ 138
Даны точки 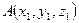 ,
, 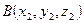 и
и 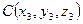 . Уравнение плоскости проходящей через эти точки имеет вид:
. Уравнение плоскости проходящей через эти точки имеет вид:
$$$ 139
Найти расстояние от точки 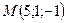 до плоскости
до плоскости 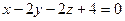
$$$ 140
Даны плоскости 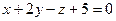 ,
, 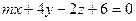 . При каком значении
. При каком значении 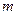 эти плоскости параллельны
эти плоскости параллельны
$$$ 141
Даны плоскости 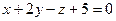 ,
, 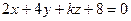 . При каком значении
. При каком значении 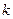 эти плоскости перпендикулярны
эти плоскости перпендикулярны
$$$ 142
Каноническое уравнение прямой 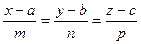 , тогда прямая параллельна вектору
, тогда прямая параллельна вектору
$$$ 143
Написать каноническое уравнение прямой, проходящей через точку 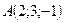 параллельно вектору
параллельно вектору 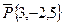
$$$ 144
Написать уравнение прямой, проходящей через точки 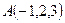 ,
, 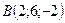
$$$ 145
Дано каноническое уравнение прямой 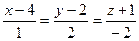 , тогда параметрическое уравнение имеет вид
, тогда параметрическое уравнение имеет вид
$$$ 146
Написать параметрическое уравнение прямой, проходящей через точки 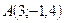 ,
, 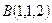
$$$ 147
Даны прямая 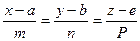 и плоскость
и плоскость 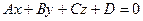 , они параллельны, если
, они параллельны, если
$$$ 148
Даны прямая 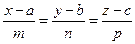 и плотность
и плотность 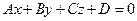 . Прямая и плоскость перпендикулярны, если
. Прямая и плоскость перпендикулярны, если
$$$ 149
Найти точку пересечения прямой 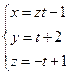 с плоскостью
с плоскостью 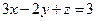
$$$ 150
Найти точку пересечения прямой 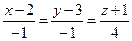 с плоскостью
с плоскостью 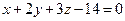
Ведение в анализ
$$$ 151
Вычислить 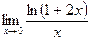
$$$ 152
Вычислить 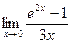
$$$ 153
Вычислить 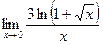
$$$ 154
Вычислить 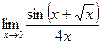
$$$ 155
Найти точки разрыва функции 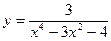
$$$ 156
Найти точки разрыва функции 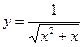
$$$ 157
Найти вертикальную асимптоту для графика функции 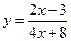
$$$ 158
Найти горизонтальную асимптоту для графика функции 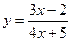
$$$ 159
Найти наклонную асимптоту для графика функции 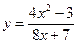
$$$ 160
Вычислить 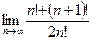
$$$ 161
Вычислить 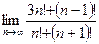
$$$ 162
Вычислить 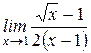
$$$ 163
Вычислить 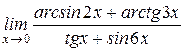
$$$ 164
Вычислить 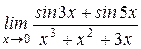
$$$ 165
Вычислить 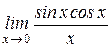
$$$ 166
Вычислить 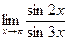
$$$ 167
Вычислить 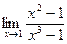
$$$ 168
Вычислить 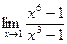
$$$ 169
Вычислить 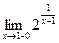
$$$ 170
Вычислить 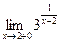
Дифференциальное исчисление функций одной переменной
$$$ 171
Производной 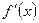 функции
функции 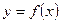 в точке
в точке 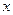 называется
называется
$$$ 172
Уравнение касательной к графику функции 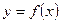 в точке
в точке 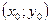 имеет вид
имеет вид
$$$ 173
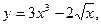
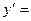
$$$ 174
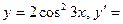
$$$ 175
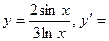
$$$ 176
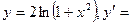
$$$ 177
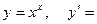
$$$ 178
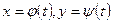 , то
, то 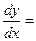
$$$ 179
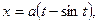
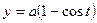 ,
, 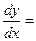
$$$ 180
Дифференциалом функции в данной точке называется
$$$ 181
Найти дифференциал функции 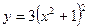
$$$ 182
Найти дифференциал функции 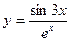
$$$ 183
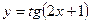
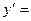
$$$ 184
Найти 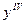 от
от 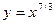
$$$ 185
Найти 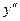 от
от 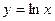
$$$ 186
Найти 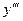 от
от 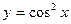
$$$ 187
Найти 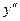 от
от 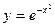
$$$ 188
Найти 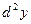 от
от 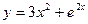
$$$ 189
Найти интервал возрастания функции 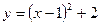
$$$ 190
Найти интервал убывания функции 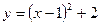
$$$ 191
Найти экстремумы функции 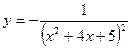
$$$ 192
Найти критические точки функции 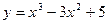
$$$ 193
Найти критические точки функции 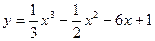
$$$ 194
Найти интервалы возрастания функции 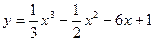
$$$ 195
Найти интервалы убывания функции 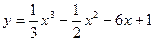
$$$ 196
Найти экстремум функции 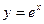
A) нет экстремума
$$$ 197
Найти вертикальную асимптоту для графика функции 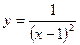
$$$ 198
Найти вертикальную асимптоту для графика функции 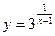
$$$ 199
Найти вертикальную асимптоту для графика функции 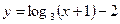
$$$ 200
Найти вертикальную асимптоту графика функции 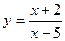
$$$ 201
Найти предел по правилу Лопиталя 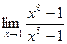
$$$ 202
Найти предел по правилу Лопиталя 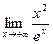
$$$ 203
Найти предел по правилу Лопиталя 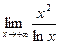
$$$ 204
Найти предел по правилу Лопиталя 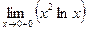
$$$ 205
Найти 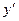 от
от 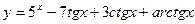
$$$ 206
Найти 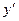 от
от 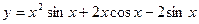
$$$ 207
Найти 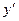 от
от 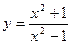
$$$ 208
Найти 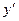 от
от 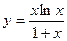
$$$ 209
Найти 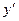 от
от 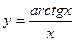
$$$ 210
Найти 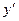 от
от 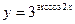
$$$ 211
Найти 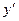 от
от 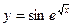
$$$ 212
Найти 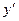 от
от 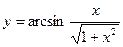
$$$ 213
Найти производную 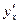 от неявной функции
от неявной функции 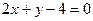
$$$ 214
Найти 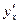 от неявной функции
от неявной функции 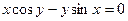
$$$ 215
Найти 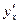 от неявной функции
от неявной функции 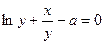
$$$ 216
Найти производную от функции, заданной параметрически 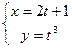
$$$ 217
Найти производную от функции, заданной параметрически 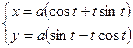
$$$ 218
Найти производную от функции, заданной параметрически 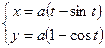
$$$ 219
Найти производную 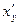 обратной функции
обратной функции 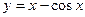
$$$ 220
Найти производную 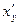 обратной функции
обратной функции