Дифференциальные уравнения.

Дифференциальным уравнением называют уравнения, содержащие не неизвестные числа х, у, и так далее, а

Неизвестную функцию у(х),

независимую переменную - х и производные от функции у(х) - y'(х), у''(х) и более высокие производные порядка (n).

В общем случае дифференциальное уравнение записывают в виде

f{х,у(х),y'(х), ... y(ⁿ)(х)} = 0.

Например уравнение х + у*у' = 4.

В простейшем случае дифференциальное уравнение содержит только саму производную

Y’ = 10

Решить дифференциальное уравнение, значит найти такую функцию Y(x), которая обращает исходное уравнение в тождество.

Последнее уравнение можно решить - простым интегрированием - иными словами необходимо записать первообразную функцию для постоянной величины. Это будет функция Y = 10x + С. Действительно производная от (10x + С)’= 10.

10 тождественно равно 10.

Основной закон механики в физике по своей математической сути является дифференциальным уравнением относительно координаты тела х(t). Так как ускорение а(t) = V'(t) = x ''(t) - является первой производной от скорости и второй производной от координаты, то имеем: x''(t) =ΣF / m = mg / m = 9,8 = 10.

(Для свободного падения под действием силы тяжести x''(t) = g )

Именно интегрированием получаются основные кинематические формулы…

	…………………………………………
	………………………………………… ………………………………………… …………………………………………

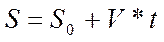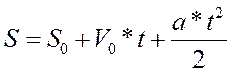Для колебания груза на пружине

m*x''(t) = - k*x(t).

Для тела падающего в среде с силой сопротивления

m*V'(t) = mg - 6*π*η*r*V(t).

Более сложный тип уравнения y’ = f(x)

В таком случае решение также находится прямым интегрированием… Y(x) =∫ f(x)dx = F(x) + C.

Например : x³*y' = 7.

Выражая отсюда y' имеем y' = 7*x^-3. Чтобы найти y(x) надо, по сути, найти интеграл

∫ 7*x^-3 dx = - 7*(х ^-2) / 2 + С.

Таким образом, найденная функция y(x) и есть решение дифференциального уравнения.

Могут быть два вида решений: общее и частное решение. В последнем примере y = - 7*(х ^-2) / 2 + С - это общее решение. Оно содержит произвольную постоянную С (причем число произвольных постоянных соответствует порядку дифференциального уравнения).

Частное решение находят из общего решения путем подстановки в общее решение НАЧАЛЬНЫХ УСЛОВИЙ типа y(x₀) = y₀.

Общее решение дифференциального уравнения соответствует множеству функций F(x), в которые входит произвольная постоянная С.

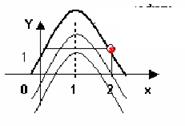
Частное решение - это какая то одна функция, график которой проходит через точку на плоскости XY, заданную начальными условиями.

Решим более сложный пример:

x*y*y' = 3.

Приведем его к виду:

g(y)dy = f(x)dx,

чтобы было можно проинтегрировать и левую и правую части!

Такой метод и называется методом разделения переменных.

В случае если уравнение явно содержит производную y' необходимо умножить обе части уравнения на dx и учесть, что y'dx это дифференциал функции dy (y'dx = dy).

Тогда получим : x*y*dy = 3* dx.

Теперь следует разделить правую и левую части на x: y*dy = 3* dx/х. Так получаются выражения, которые можно интегрировать: ∫y*dy = ∫3* dx/х. Общее решение будет: y = ( 6 Lnx + C )^1/2 .

Введение в статистику

Случайным событием называют событие, которое может произойти или нет в зависимости от множества случайных факторов, которые учесть практически невозможно.

Вероятностью такого события называют отношение числа наблюдений, в которых это событие произошло (m) к общему числу испытаний (n):

P = m/n.

Число испытаний при этом должно быть достаточно большим.

Приведите численный пример на иллюстрацию данного определения.

Так как ни n, ни mне могут быть отрицательными, причем всегда n > m, то вероятности любого события заключается в интервале

0 ≤ P ≤ 1.

Вероятность невозможного события равна 0, достоверного события равна 1.

Для попарно несовместимых равновероятных событий

Р = 1/К,

где К - число возможных исходов.

Выпишите и проиллюстрируйте теоремы сложения и умножения вероятностей, дайте понятие условной вероятности………………..

……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………