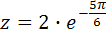Приложения опредеделенного интеграла. Площадь плоской фигуры.

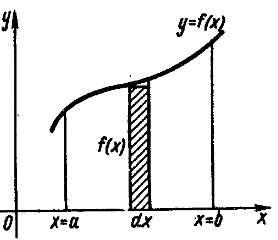Найдем площадь S криволинейной

трапеции, ограниченной кривой y=ƒ (x), осью Ox и двумя прямыми x=a и x=b, где a≤x≤b, ƒ (x)≥0 , S – площадь прямоугольника с основанием dx и высотой ƒ (x), т.е. dS= ƒ (x) dx Интегрируя это равенство в пределаот a до b, получим

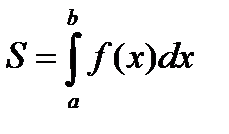Если криволинейная трапеция ограниченная кривой y= ƒ(x), осью

Ox и прямыми x=a и x=b, лежит под осью Ox, то

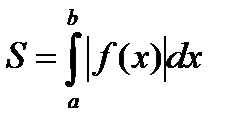
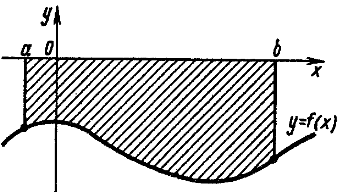
Если фигура, ограниченная кривой ƒ(y), осью Ox и прямыми

x=a и x= b, расположена по обе стороны от оси Ox, то

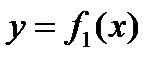
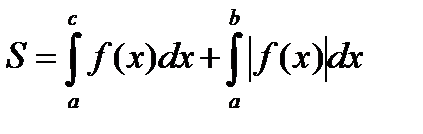
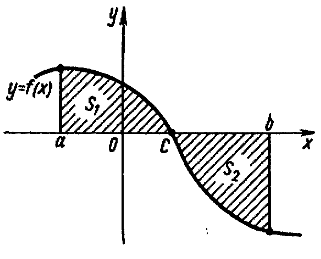
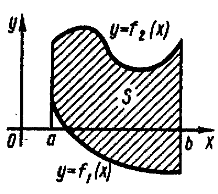
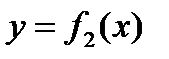Фигура S ограничена двумя пересекающимися кривыми

и и прямыми x=a и x=b, где a≤x≤b и

Площадь вычисляется по формуле

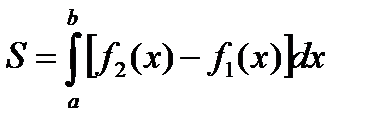
Примеры.

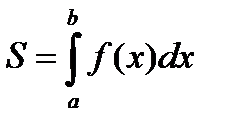
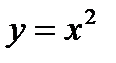
1. 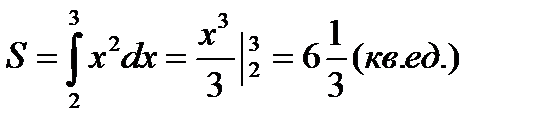Вычислить площадь криволинейной трапеции, ограниченной параболой и прямыми х=2 и х=3 и осью Ox. По формуле

Находим:

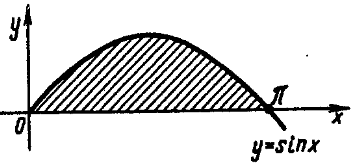
2. 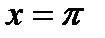y=sinx, y=0 и

Искомая площадь ограничена полуволной синусоиды и осью Ох.

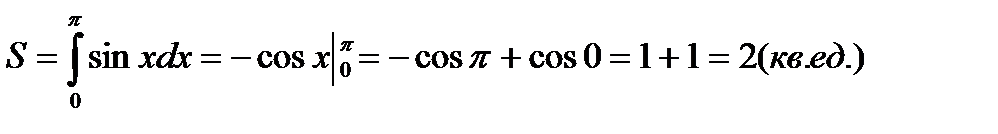
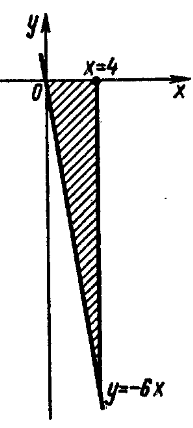
3. у=-6х, у=0 и х=4.

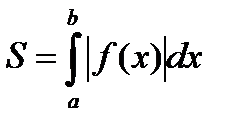Фигура расположена под осью Ох. Следовательно, ее

площадь находим по формуле

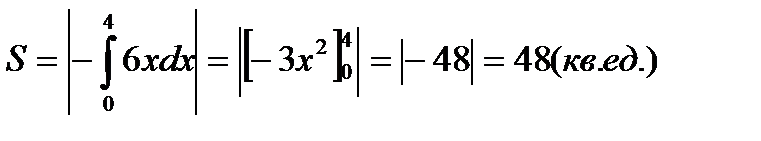
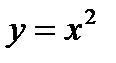
4. 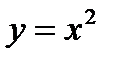и у=2х.

Данная фигура ограничена параболой и

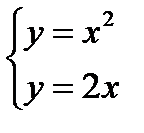прямой у=2х. Для определения точек пересечения заданных линий решим систему уравнений :

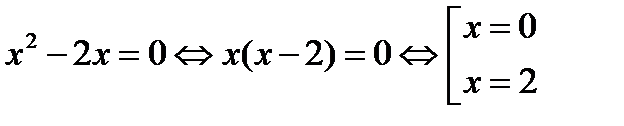
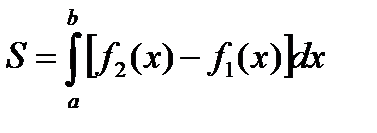откуда находим

Используя для нахождения площади формулу

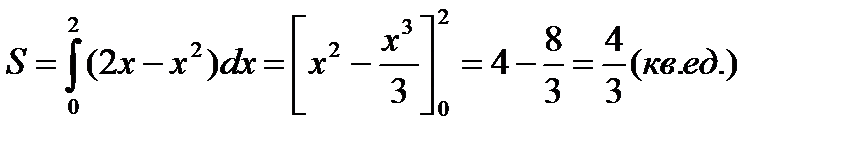получим

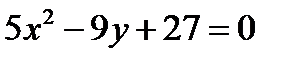
5. 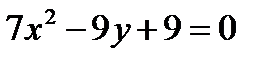Фигура, ограничена линиями и

Найдем точки пересечения данных парабол, выразим из каждого уравнения переменную уи решим систему уравнений:

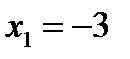
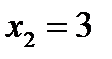
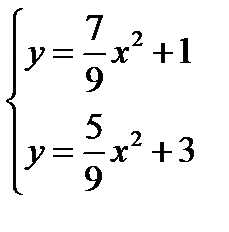
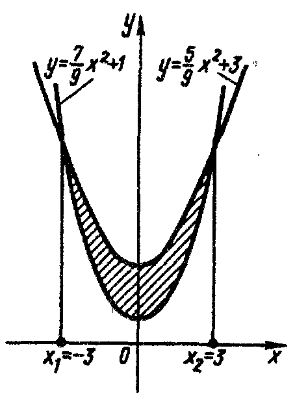откуда

Так как фигура симметрична относительно оси Оу, то найдем

половину ее площади, взяв пределы интегрирования от 0 до 3, и

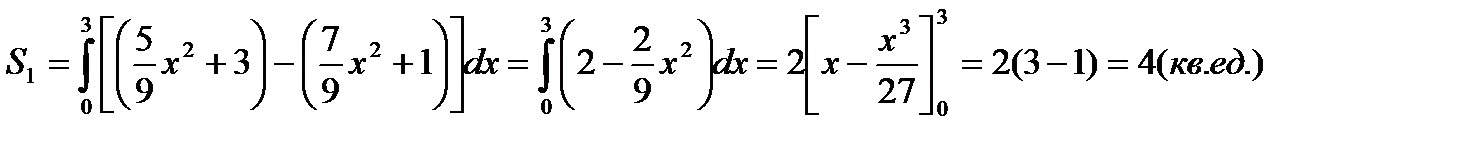результат удвоим:

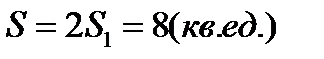
Комплексные числа.

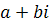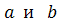Комплексными числами называются числа вида , где - действительные числа. Число 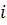, определяемое равенством 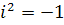, называется мнимой единицей.

Запись комплексного числа в виде 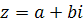называется алгебраической формой комплексного числа.

При 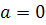комплексное число обращается в чисто мнимое число .

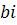Комплексное число 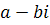называется комплексно сопряженным с числом 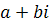и обозначается .

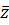Комплексные числа 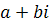, и 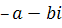, называются противоположными.

Модулем комплексного числа называется число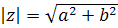

Действия над комплексными числами, заданными в алгебраической форме:

Сложение: (a + bi) + (c + di) = (a + c) + (b + d)i.

Вычитание: (a + bi) − (c + di) = (a − c) + (b − d)i.

Умножение: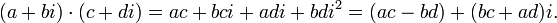

Деление:

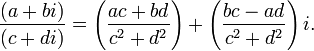
Тригонометрическая форма комплексного числа.

Например.Представить комплексное число 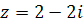в тригонометрической форме.

Решение: здесь 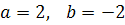, найдем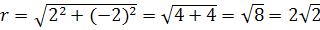

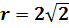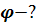, точка с координатами 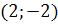находится в 4 четверти координатной плоскости, 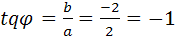, следовательно 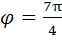, данное число в тригонометрической форме будет иметь вид:

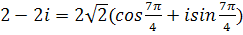
Действия над комплексными числами, заданными в тригонометрической форме.

Формула Муавра.

Эта формула позволяет возводить в степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:

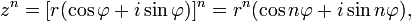
Аналогичная формула применима также и при вычислении корней n-ой степени из ненулевого комплексного числа:

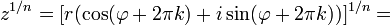
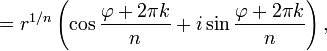
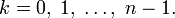
Показательная форма комплексного числа:

Тригонометрическую форму комплексного числа можно заменить показательной:

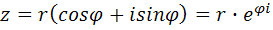
Пример.

Представить число 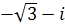в тригонометрической и показательной форме.

Решение. 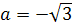, b=-1, r=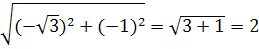

,

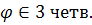
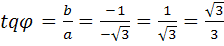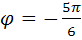
И следовательно 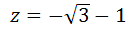=2 ;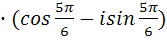

В показательной форме: