Построение прямой на плоскости
Уравнение прямой на плоскости,
Проходящей через данную точку параллельно заданному вектору
Пусть 
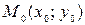 – фиксированная точка плоскости,
– фиксированная точка плоскости, 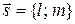 – ненулевой вектор. Тогда уравнение прямойна плоскости, проходящей через точку
– ненулевой вектор. Тогда уравнение прямойна плоскости, проходящей через точку 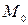 параллельно вектору
параллельно вектору 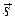 (рис. 1), в векторной форме запишется так:
(рис. 1), в векторной форме запишется так:
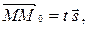 | (1) |
где параметр 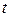 принадлежит множеству действительных чисел; принадлежит множеству действительных чисел; 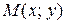 – произвольная точка этой прямой; – произвольная точка этой прямой; 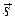 – (в данном случае) направляющий вектор полученной прямой. – (в данном случае) направляющий вектор полученной прямой. | 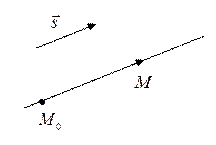 Рис. 1 Рис. 1 |
Параметрические уравнения прямой на плоскости
Перепишем уравнение (1) в координатной форме:
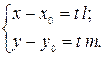 | (1а) |
Выполнив элементарные преобразования, получим параметрические уравнения прямой:
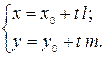 | (2) |
Каноническое уравнение прямой на плоскости
Исключив из системы уравнений (2) параметр t, получим каноническое уравнение прямой на плоскости, проходящей через заданную точку 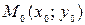 параллельно вектору
параллельно вектору 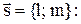
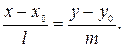 | (3) |
Уравнение прямой на плоскости,
Проходящей через две заданные точки
Предположим, что на плоскости заданы две различные точки: 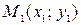 и
и 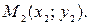 В этом случае вектор
В этом случае вектор 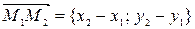 будет направляющим вектором единственной прямой, проходящей через две заданные точки, каноническое уравнение такой прямой запишем в виде:
будет направляющим вектором единственной прямой, проходящей через две заданные точки, каноническое уравнение такой прямой запишем в виде:
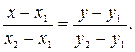 | (4) |
Общее уравнение прямой на плоскости
Используя свойство пропорции, преобразуем уравнение (4):
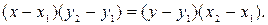 | (4а) |
Раскроем скобки и перепишем уравнение (4а), введя следующие обозначения: 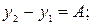
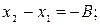
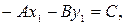 в результате чего получим:
в результате чего получим:
| Ax + By + C = 0. | (5) |
Утверждение 1.Если в уравнении (5) 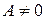 или
или 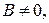 то уравнение (5) на плоскости определяет некоторую прямую и называется при этом общим уравнением прямой на плоскости.
то уравнение (5) на плоскости определяет некоторую прямую и называется при этом общим уравнением прямой на плоскости.
1.6. Уравнение прямой «с угловым коэффициентом»
Из общего уравнения прямой (5) легко получить уравнение вида
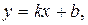 | (6) |
т. е. уравнение прямой на плоскости «с угловым коэффициентом 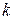 », где
», где 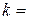 tg
tg 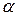 (
( 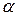 – угол, образованный данной прямой с положительным направлением оси абсцисс). Величина b в уравнении (6) называется начальной ординатой, так как это число по абсолютной величине равно длине отрезка, отсекаемого прямой на оси ординат. Если прямая проходит через начало координат
– угол, образованный данной прямой с положительным направлением оси абсцисс). Величина b в уравнении (6) называется начальной ординатой, так как это число по абсолютной величине равно длине отрезка, отсекаемого прямой на оси ординат. Если прямая проходит через начало координат 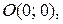 то
то 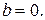
Особые случаи расположение прямой на плоскости
Исследуем общее уравнение прямой (5):
1) при 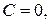
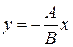 прямая проходит через начало координат;
прямая проходит через начало координат;
2) при 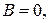
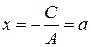 прямая параллельна оси Ох;
прямая параллельна оси Ох;
3) при 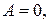
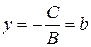 прямая параллельна оси Оу;
прямая параллельна оси Оу;
4) при 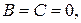
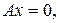
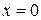 получаем уравнение оси Оу;
получаем уравнение оси Оу;
5) при 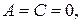
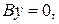
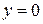 получаем уравнение оси Ох.
получаем уравнение оси Ох.
Построение прямой на плоскости.
Уравнение прямой на плоскости «в отрезках»
Помимо известных способов построения прямой на плоскости – по двум точкам, по данной точке и «наклону» прямой – удобно пользоваться так называемым уравнением прямой «в отрезках» на координатных осях:
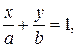 | (7) |
которое может быть составлено для любой прямой, не проходящей через начало координат.
Пример. Построить прямую, заданную уравнением «в отрезках» на осях: 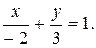 Решение. Решение.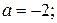 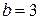 (рис. 2). (рис. 2). |  Рис. 2 Рис. 2 |
2. ПРЯМЫЕ НА ПЛОСКОСТИ: ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
Утверждение 2.Пусть на плоскости заданы две прямые: 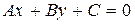 и
и 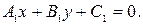 В этом случае выполняется одно и только одно из трех условий:
В этом случае выполняется одно и только одно из трех условий:
1) прямые не имеют общих точек 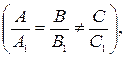 при этом система линейных алгебраических уравнений
при этом система линейных алгебраических уравнений 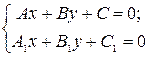 несовместна (имеет пустое множество решений);
несовместна (имеет пустое множество решений);
2) прямые имеют единственную общую точку 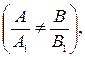 при этом система линейных алгебраических уравнений
при этом система линейных алгебраических уравнений 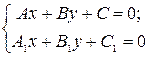 имеет единственное решение
имеет единственное решение 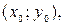 которое может быть найдено, например, по формулам Крамера:
которое может быть найдено, например, по формулам Крамера:
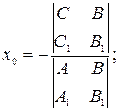 | (11) | 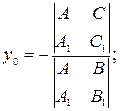 | (12) |
3) прямые совпадают 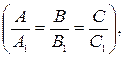 при этом система линейных алгебраических уравнений
при этом система линейных алгебраических уравнений 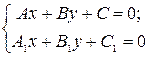 не определена (имеет бесконечно много решений).
не определена (имеет бесконечно много решений).
