Уравнения Максвелла в интегральной форме
Введение тока смещения позволило Максвеллу блестяще завершить единую теорию электромагнитного поля. Эта теория не только объяснила все разрозненные явления электричества и магнетизма, но и предсказала ряд новых явлений, которые были подтверждены впоследствии.
Эта теория базируется на единой системе четырех уравнений Максвелла, которая может быть записана в интегральной и дифференциальной форме.
Уравнения Максвелла в интегральной форме:
1. 
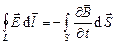; (5.3)
2. 
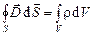; (5.4)
3. 
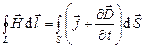; (5.5)
4. 
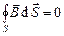. (5.6)
Содержание каждого из этих уравнений заключается в следующем:
1. Циркуляция вектора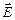 
по любому замкнутому контуру равна со знаком минус производной по времени от магнитного потока через любую поверхность, ограниченную данным контуром. При этом под 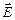понимается не только вихревое электрическое поле, но и электростатическое (циркуляция такого поля равна нулю). Отсюда следует, что если существует переменное во времени магнитное поле 
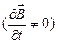, то оно порождает электрическое поле, циркуляция которого не равна нулю. Это электрическое поле имеет индукционное происхождение, т. е. будет вихревым, в отличие от потенциального ‑ электростатического. В частности, это означает, что силовые линии вихревого поля будут замкнутыми;
2. Поток вектора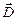 
сквозь любую замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью. (Фактически это теорема Гаусса для поля заряда, распределенного внутри замкнутой поверхности с объемной плотностью заряда 
);
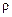3. Циркуляция вектора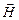 
по любому замкнутому контуру равна полному току (току проводимости и току смещения) через произвольную поверхность, ограниченную данным контуром. Данное уравнение является обобщением теоремы полного тока, но с учетом тока смещения;
4. Поток вектора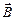 
сквозь произвольную замкнутую поверхность всегда равна нулю. Данное уравнение постулирует отсутствие в природе «магнитных» зарядов. (Это теорема Гаусса для магнитного поля).
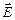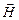Из уравнений Максвелла для циркуляции векторов и следует, что электрическое и магнитное поле нельзя рассматривать как независимые: изменение во времени одного из них приводит к появлению другого. Таким образом, следует рассматривать единое электромагнитное поле.
В то же время в случае стационарных поле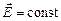й ( 
и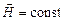 
) система уравнений Максвелла распадается на две группы независимых уравнений:
; 
;
; .
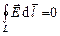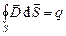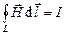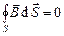В этом случае электрическое и магнитное поля независимы друг от друга, поэтому могут рассматриваться физически и математически раздельно.
Само разделение поля на две части ‑ чисто электрическое и чисто магнитное является относительным. В самом деле, по принципу относительности все физические законы, в том числе и электромагнитные, являются инвариантными (т. е. имеют одинаковый вид, описываются одинаковыми уравнениями) во всех инерциальных системах отсчета. Поэтому если электрические заряды неподвижны относительно данной системы отсчета, то в ней они создают только электрическое поле. В другой же системе отсчета, относительно которой эти заряды подвижны, они создают и электрическое, и магнитное поля, поскольку, как мы знаем, магнитное поле создается движущимися зарядами. Точно так же постоянный ток в неподвижном проводе создает постоянное магнитное поле. Однако в другой инерциальной системе, в которой провод движется, магнитное поле будет меняться, и оно вызовет вихревое электрическое поле.
Следует подчеркнуть, что уравнения Максвелла в интегральной форме (5.3. – 5.6.) справедливы только для изотропнойсреды, т. е. такой среды, свойства которой одинаковы во всех направлениях. В общем случае анизотропнойсреды, т. е. такой, свойства которой зависят от направления, эти уравнения усложняются.
Вместе с системой уравнений Максвелла обычно записывается выражение для энергии электромагнитного поля:
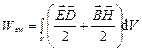, (5.7)
так как объемная плотность энергии электрического и магнитного полей определяется формулой
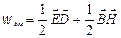. (5.8)
Векторы напряженности электрического поля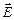 
и индукции магнитного поля 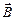взаимно-перпендикулярны друг другу. Векторы индукции электрического поля 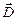(который направлен в ту же сторону, что и вектор 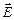), и напряженности магнитного поля 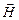(направленный так же, как и вектор 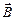) также взаимно-перпендикулярны. Направление магнитного поля, созданного током смещения, соответствует правилу правого винта.