Оценка случайной погрешности.

Случайную погрешность величины X можно оценить, только проведя многократное измерение X – не менее четырёх. Это означает, что процедуру измерения X надо проделать не менее четырёх раз, причём обязательно в одних и тех же условиях. Если бы никакие случайные факторы не влияли на результаты измерений, то, сколько бы раз не повторялась процедура измерения X, все результаты были бы совершенно идентичными. Наличие случайных факторов приводит к тому, что серия из n измерений даёт n разных значений величины X: (x₁, x₂, ..., x_n)[1]. То, насколько велик разброс в этих n числах, и определяет случайную погрешность. Формула, по которой оценивают случайную погрешность D_с(x), имеет вид:

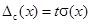. (5.1)

Здесь величина t называется коэффициентом Стьюдента. Как его определить, рассмотрено в пункте 6. Величина s(x) называется среднеквадратичным (или стандартным) отклонением и определяется выражением

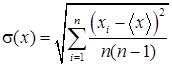, (5.2)

где <x> – средний результат измерения, то есть среднее арифметическое из n чисел x₁, x₂, ..., x_n:

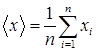. (5.3)

Из формулы (5.2) следует, что стандартное отклонение s(x) уменьшается с ростом объёма серии n. В пункте 6 отмечается, что и коэффициент Стьюдента тоже уменьшается с ростом n. Поэтому из формулы (5.1) вытекает: чем больше объём серии, тем меньше случайная погрешность. Обычно объём серии выбирают так, чтобы случайная погрешность была в три-пять раз меньше приборной погрешности.

Доверительная вероятность и коэффициент Стьюдента

Будем в этом пункте считать, что приборная погрешность равна нулю. Тогда 2D_c – это ширина доверительного интервала. В пункте 1 предполагалось, что в центре доверительного интервала находится истинное значение x измеряемой величины X. Истинное значение, однако, неизвестно, поэтому передвинем доверительный интервал так, чтобы в центре его находилось среднее значение результатов измерения <x>. Так как действие случайных факторов непредсказуемо, то разница между x и <x> может оказаться как меньше величины D_c, рассчитываемой по формуле (5.1), так и больше.

Определение 4.

Вероятность того, что истинное значение x измеряемой величины X принадлежит доверительному интервалу шириной 2D_с с центром в точке <x>, называется доверительной вероятностью или надёжностью измерений.

Как уже отмечалось в пункте 5, с ростом коэффициента Стьюдента растёт случайная погрешность, а значит, растёт ширина доверительного интервала. Ясно, что чем шире доверительный интервал, тем больше и доверительная вероятность. Поэтому всегда можно подобрать такое значение коэффициента Стьюдента, которое обеспечивает требуемое значение надёжности измерений, то есть доверительной вероятности a. Результаты исследования этой проблемы, полученные Стьюдентом, приведены в таблице 6.1.

Таблица 6.1

Коэффициенты Стьюдента

Объём серии n	Доверительная вероятность a
0,5	0,6	0,7	0,8	0,9	0,95	0,98	0,99
	0,77	0,98	1,2	1,6	2,4	3,2	4,5	5,8
	0,74	0,94	1,2	1,5	2,1	2,8	3,7	4,6
	0,73	0,92	1,2	1,5	2,0	2,6	3,4	4,0
	0,72	0,90	1,1	1,4	1,9	2,4	3,1	3,7
	0,71	0,90	1,1	1,4	1,9	2,4	3,0	3,5
	0,71	0,89	1,1	1,4	1,8	2,3	2,9	3,4
	0,70	0,88	1,1	1,4	1,8	2,3	2,8	3,3
	0,69	0,87	1,1	1,3	1,8	2,1	2,6	3,0
	0,69	0,86	1,1	1,3	1,7	2,1	2,5	2,9

Как видно из этой таблицы, коэффициент Стьюдента t зависит от двух факторов – от заданной надёжности измерений a и от объёма серии измерений n. С ростом надёжности коэффициент Стьюдента быстро нарастает, с ростом объёма серии – медленно падает.

Пример. Требуется измерить сопротивление резистора R с надёжностью a = 0,95. Проделана серия из 10 измерений сопротивления, средний результат получился такой: <R> = 42,3 кОм при стандартном отклонении s(R) = 0,22 кОм. Тогда из таблицы 6.1 следует, что t = 2,3, и в результате случайная погрешность равна: D_с(R) = 2,3×0,22 = 0,5 кОм.