I. Метод непосредственного интегрирования

Нахождение интегралов с использованием основных свойств неопределённых интегралов и таблицы простейших (табличных) интегралов называется непосредственным интегрированием.

Свойства неопределённого интеграла

1. d ò f (x)dx = f (x)dx .

2. òd (f (x)) = f (x) +C .

Эти свойства непосредственно следуют из определения первообразной.

3. Если k – постоянная величина, то

òkf (x)dx = k ò f (x)dx , k – постоянная.

Постоянный множитель выносится за знак интеграла.

4. ò( f₁(x) + f ₂ (x))dx = ò f₁(x)dx + ò f ₂ (x)dx .

Интеграл от алгебраической суммы двух (или нескольких) функций равен сумме интегралов от этих функций (при условии их существования).

Рассмотрим несколько примеров нахождения неопределённых интегралов, используя только их свойства и таблицу основных интегралов.

Приведённые ниже интегралы (1 – 6) содержат степенную функцию x^a ; к такому виду следует приводить подынтегральную функцию, используя свойства степеней:

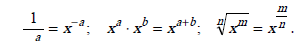
Нахождение таких интегралов основано на использовании формулы 1 из таблицы интегралов

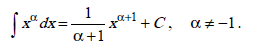
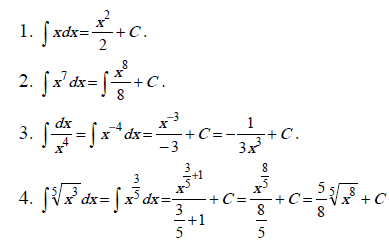
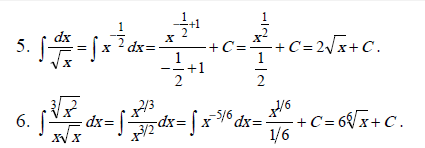
Нахождение интегралов (7 – 10) предполагает использование первых двух свойств неопределённого интеграла.

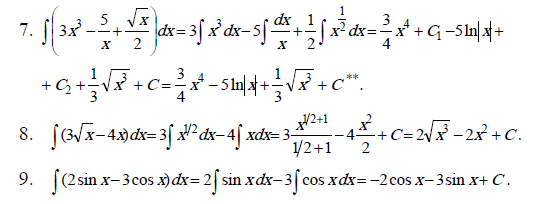
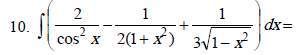
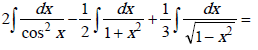
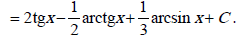
Метод непосредственного интегрирования может удачно сочетаться с тождественными преобразованиями подынтегральной функции, которые сводят искомый интеграл к одному или нескольким табличным интегралам. В примерах (11 – 19) используются тождественные преобразования: раскрытие скобок (11, 12, 15, 16), почленное деление слагаемых числителя дроби на общий знаменатель (13, 14, 15, 16);

группировка слагаемых (18); применение тригонометрических формул (17).

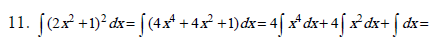
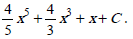
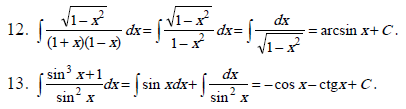
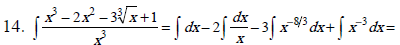
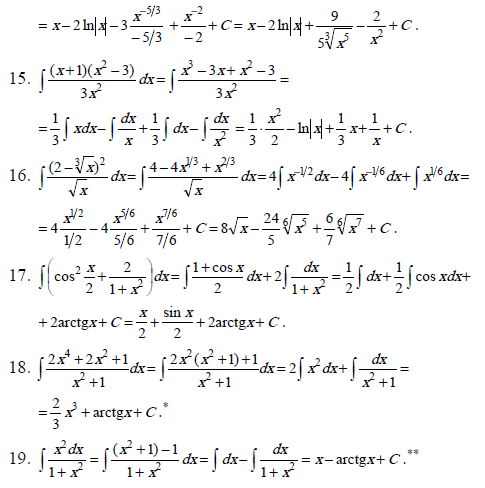
II.Метод ввода новой переменной

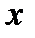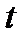В некоторых случаях нахождение интеграла упрощается при переходе к другой переменной интегрирования. При этом если исходная и новая переменные и связаны соотношением 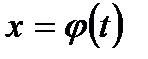, где 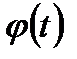- обратимая дифференцируемая функция, то для интегралов справедливо равенство

,

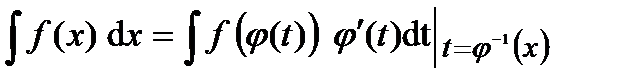в правой части которого после вычисления интеграла следует сделать обратную замену .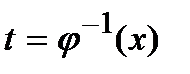

В частности, используя замену 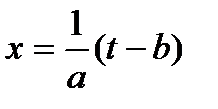(или 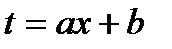), получаем формулу

,

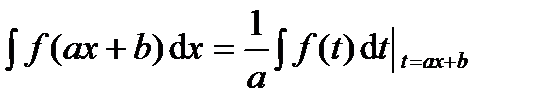позволяющую обобщить табличные интегралы. Например:

( ),

,

,

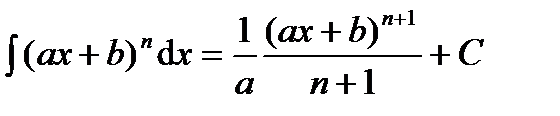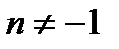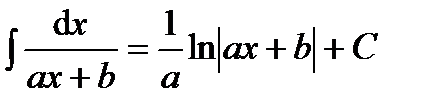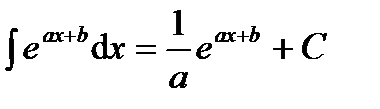где 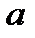и 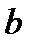- произвольные постоянные, .

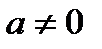Примеры. Найдем интегралы, применяя полученные формулы:

а) ;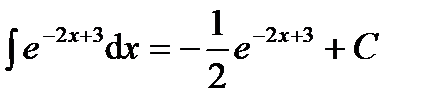

б) ;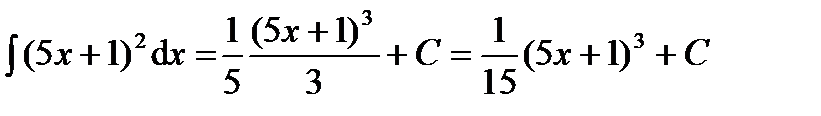

в) ;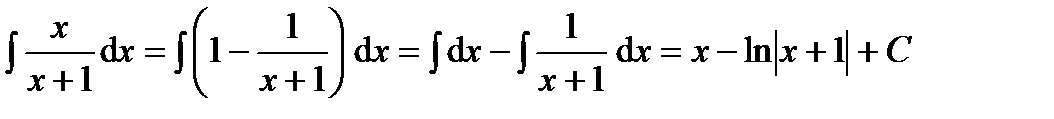

г) интеграл 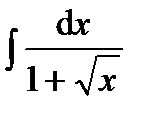найдем, сделав замену 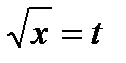, 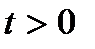. Тогда

,

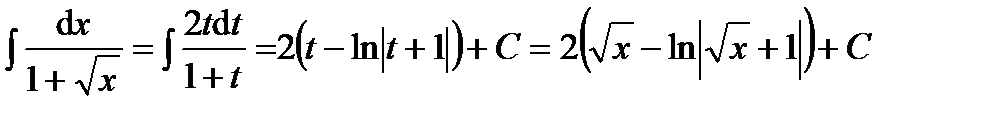где использован результат примера в);

д) .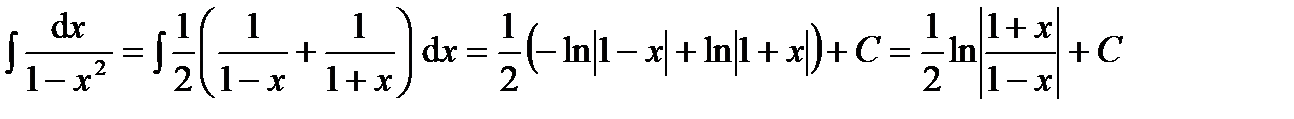

Задание для практической работы

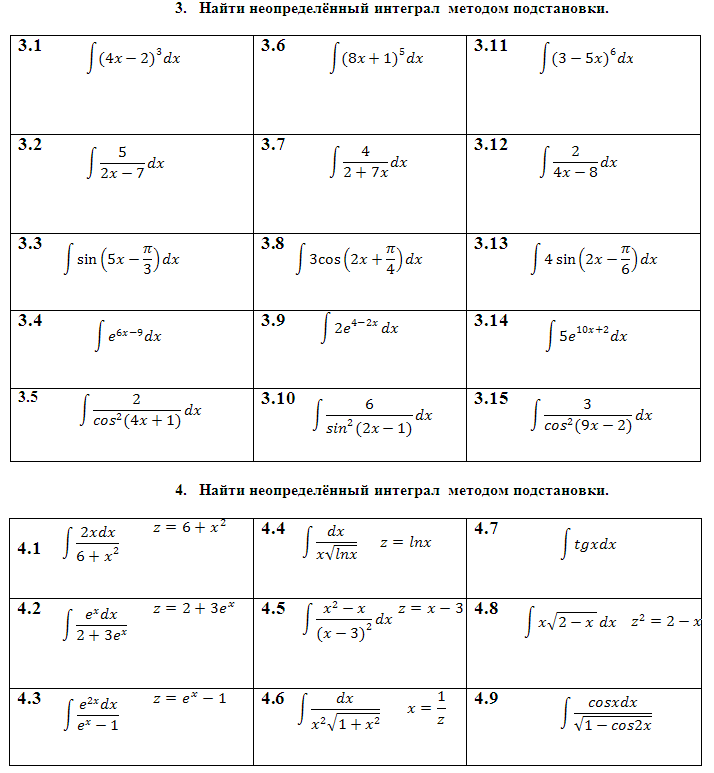
1. Найти неопределённый интеграл, используя таблицу интегралов

Контрольные вопросы

1. Какие методы интегрирования вам известны?

2. Запишите свойства неопределённого интеграла.

3. Запишите по памяти табличные интегралы

Практическое занятие №7

Тема: Интегрирование по частям

Цель: Проверить на практике умение находить неопределённый интеграл методом интегрирования по частям.

Задачи:

• развитие творческого профессионального мышления;

• познавательная мотивация;

• овладение языком науки, навыки оперирования понятиями;

• углубление теоретической и практической подготовки;

• развитие инициативы и самостоятельности студентов.

Обеспечение практического занятия:

Теоретический материал методической рекомендации к практической работе.