Эксплуатационные режимы протяжённой электропередачи

Работа № 4

Цель работы: научиться исследовать рабочие режимы протяжённой межсистемной линии электропередачи (ЛЭП); оценивать мощности устройств компенсации (КУ, УКРМ) или источников (ИРМ) реактивной мощности по концам электропередачи; определять потребность питающей и приёмной систем в реактивной мощности в зависимости от передаваемой по линии активной мощности.

Программа работы

1. Выполните задание на подготовительную работу.

2. Подготовьте файл исходных данных программы “РЕЖИМ” для моделирования электрической системы, состоящей из электрической станции, линии электропередачи и шин бесконечной мощности (приёмная система).

3. Определите распределение модуля напряжения вдоль линии в зависимости от передаваемой по ней по ней активной мощности.

4. Для каждого исследуемого режима определите значения реактивных мощностей по концам электропередачи и угол сдвига между векторами напряжения и тока вдоль линии, обращая внимание на их знаки.

5. Постройте экспериментальные и расчётные зависимости модуля напряжения вдоль линии (U(l_x)) для различных значений передаваемой активной мощности.

6. Постройте экспериментальные и расчётные зависимости реактивной мощности в начале (Q_н(P)) и в конце (Q_к(P)) линии от величины передаваемой активной мощности.

7. Для каждого значения передаваемой активной мощности постройте векторную диаграмму , содержащую напряжения и токи в начале, середине и конце линии.

8. Составьте отчёт по работе.

Задание на подготовительную работу

1. Изучите описание лабораторной работы.

2. Ознакомьтесь с разделами литературы : [2] с.6-14; [7] с.99-116,323-343; [8] с.37-42,75-78.

3. Ответьте на контрольные вопросы.

4. Вычислите :

- волновое сопротивление Z_в, натуральную мощность P_нат , волновую длину линии l;

- параметры “П” - схем замещения участка линии длиной 100 км;

5. Для линии без потерь при равенстве модулей напряжений по концам линии номинальному U_н=U_к=U_ном рассчитайте зависимости :

- реактивных мощностей по концам линии от передаваемой по ней мощности Q_н(P), Q_к(P);

- зависимость U(l_x) модуля напряжения от расстояния от начала линии l_x для четырёх значений передаваемой мощности : P =0 ; P < P_нат ; P = P_нат ; P > P_нат .

6. Подготовьте таблицы для составления протокола работы и внесите в них значения вычисленных при подготовке к работе величин.

Содержание отчёта

1. Схема энергообъединения и расчётная схема модели межсистемной связи.

2. Результаты расчёта параметров модели линии.

3. Результаты измерений напряжений, токов, реактивных мощностей.

4. Расчётные и экспериментальные зависимости: Q_н(P), Q_к(P) ; U(l_x).

5. Векторные диаграммы токов и напряжений в начале, середине и конце линии для четырёх значений передаваемой мощности.

Пояснения к работе

Линии электропередачи высокого (ВН) и сверхвысокого напряжения (СВН) U_ном = 220 кВ и выше для ограничения потерь активной мощности при возникновении коронного разряда на проводах выполняются с расщеплёнными фазными проводами. При этом каждая фаза состоит из нескольких параллельных проводов. Для ЛЭП с расщеплёнными проводами характерны соотношения x^*_л»r^*_л; b^*_л»g^*_л и приближённо их можно считать линиями без потерь (r^*_л »g^*_л »0 ).

Известно [8], что ЛЭП в зависимости передаваемой по ней активной мощности может рассматриваться либо как источник, либо как потребитель реактивной мощности.

а)

б)

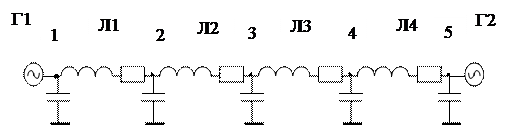Рис.4.1 . Схема энергообъединения (а) и его схема замещения (б).

Для линии без потерь с использованием обозначений рис.4.1,а можно написать :

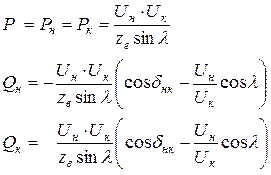. (4.1)

где: d_нк = Arg(U_н)-Arg(U_к) - угол между векторами напряжений питающей и приёмной систем; z_в 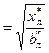,Ом - волновое сопротивление ЛЭП; l = 0,06×l, эл.градус - волновая длина ЛЭП на частоте 50 Гц (l - длина линии в км).

В случае равенства модулей напряжения по концам ЛЭП U_н=U_к=U_ном реактивные мощности реактивные мощности по концам ЛЭП одинаковы по величине и противоположны по направлению.

Если угол между векторами напряжений передающей и приёмной систем меньше волновой длины линии (d_нк<l), то передаваемая активная мощность меньше натуральной мощности линии (P<P_нат=U²_ном/z_в). При этом, линия электропередачи генерирует реактивную мощность во внешнюю сеть (Q_н <0; Q_к>0). При передаче по линии активной мощности большей, чем её натуральная (d_нк>l; P >P_нат), происходит потребление реактивной мощности линией из внешней сети (Q_н >0; Q_к<0). Наконец при передаче натуральной мощности (d_нк=l; P =P_нат) линия работает в режиме самокомпенсации реактивной мощности (Q_н=0; Q_к=0), при котором генерируемая каждым участком линии реактивная мощность им же и потребляется.

Таким образом, для поддержания заданных значений модулей напряжения необходимо иметь в начале и конце ЛЭП реверсивные источники реактивной мощности, которые могут либо потреблять, либо генерировать реактивную мощность. Такими источниками являются [2] синхронные генераторы электрических станций, мощные синхронные двигатели, синхронные компенсаторы (СК) и статические тиристорные компенсаторы (СТК).

Распределение напряжения вдоль линии зависит от загрузки линии активной мощностью. В случае линии без потерь и одинаковых модулей напряжения по концам линии (U_н=U_к=U_ном) для определения зависимости модуля напряжения U_x от расстояния от начала линии l_x,км (или l_x =0,06×l_x, эл.градус) следует задать величину передаваемой мощности P=P_н , найти величину угла (d_нк) и значение реактивной мощности Q_н из уравнений (4.1).

Далее рассмотрим участок линии длиной l_x с известными параметрами начала U_н, P_н, Q_н и неизвестными U_x, Q_x, d_x , где d_x = Arg(U_н)-Arg(U_x) - угол между векторами напряжений в начале ЛЭП и в конце рассматриваемого участка . Для нахождения неизвестных решим систему уравнений для активной и реактивной мощностей в начале этого участка :

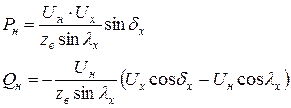(4.2)

Их совместное решение даёт :

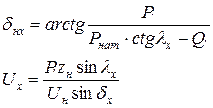(4.3)

При d_x =0 вместо второго уравнения можно использовать следующее:

(4.4)

Заметим, что при U_н=U_к у ЛЭП без потерь значения модулей напряжений, токов и реактивных мощностей симметричны относительно её середины. Направления реактивных мощностей в точках линии, симметричных относительно её середины, - противоположны. При этом реактивная мощность в средней точке линии всегда равна нулю, а угол между векторами напряжений в начале линии и в её середине равен половине суммарного угла на передаче . Тогда выражение для модуля напряжения в средней точке легко получается из последнего уравнения (4.1) :

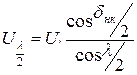(4.5)

Из сказанного следует, что наибольшее значения напряжения в средней точке соответствует режиму двустороннего питания ненагруженной ЛЭП (d_нк=0). В соответствии нормами проектирования напряжение в любой точке электрической сети не должно превышать наибольшего рабочего напряжения (для ЛЭП 330 кВ - 1,1×U_ном ; для ЛЭП 500 - 1150 кВ - 1,05×U_ном ), что накладывает ограничение на максимальную длину однородной ЛЭП (без промежуточных присоединений) до l < 600 - 650 км при частоте в сети 50 Гц и l < 500 - 550 км при частоте 60 Гц.

При увеличении передаваемой мощности сверх натуральной (d_нк>l; P >P_нат) напряжение в середине линии уменьшается и в предельном режиме, когда d_нк =90° достигает наименьшего значения:

.

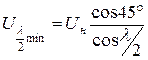Все приведённые уравнения справедливы для линии без потерь. При наличии активных сопротивлений в схеме картина распределения напряжения вдоль линии искажается тем сильнее, чем длиннее линия и ниже её номинальное напряжение.

Методические указания

Работа выполняется с использованием программы расчёта установившихся режимов работы электрических сетей “Режим”. Описание программы и правила заполнения исходных данных приведены в начале пособия .

При моделировании нагрузочных режимов межсистемной связи следует разделить линию по длине на четыре одинаковых участка, соединённых последовательно в трех промежуточных узлах. При этом расчётная схема будет содержать пять узлов и четыре ветви.

В первом и в последнем узле задаются фиксированные модули напряжения, равные номинальному напряжению линии. Балансирующим узлом назначается первый узел (отвечающего шинам питающей системы). Величина передаваемой по линии мощности P задается нагрузкой последнего узла (отвечающего шинам приемной системы).

В работе требуется исследовать следующие нагрузочные режимы:

- холостой ход (P=0);

- режим передачи мощности меньшей натуральной мощности линии (P< P_нат) 25%, 50% и 75% от P_нат;

- режим передачи натуральной мощности (P= P_нат);

- режим передачи мощности большей натуральный (P> P_нат).

Контрольные вопросы

1. В каком из рассматриваемых режимов линии электропередачи будет максимальное значение модуля напряжения в середине линии ?

2. В каком из режимов эпюра напряжений межсистемной линии не изменится , если её разомкнуть в средней точке?

3. Как определить максимальную мощность, которую можно передать по линии без потерь?

4. Как изменяется модуль напряжения вдоль линии при передаче по ней мощности меньшей, чем её натуральной мощности? Чем опасен такой режим?

5. Как изменяется модуль напряжения вдоль линии при передаче по ней мощности большей, чем её натуральная мощность? Почему такой режим экономически менее выгоден, чем режим передачи натуральной мощности?

6. Как изменяются углы сдвига векторов тока и напряжения в начале, середине и конце линии при увеличении передаваемой по ней активной мощности?

7. Как изменяется характер реактивной мощности в начале, середине и конце линии при увеличении передаваемой по ней активной мощности?

Таблица 4.1

Варианты заданий

Номер варианта	Длина линии l	Номинальное напряжение Uном	r*л	x*л	b*л
-	км	кВ	Ом/100км	МкСим/100км
			2,9	29,9
			1,8	28,0
			0,75	26,0
			2,0	29,5
			1,5	27,9
			0,75	22,2
			3,7	32,1
			3,0	31,8