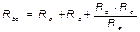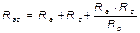Преобразования в линейных электрических цепях

Соединение резисторов.

Существует два вида соединения резисторов: последовательное и параллельное (рис. 2.17).

При последовательном соединении резисторов (рис. 2.17а) через все резисторы протекает один и тот же ток I, то есть:

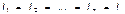
Напряжение же U равно сумме падений напряжений на сопротивлениях:

Общее сопротивление R рассчитывается

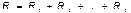
При параллельном соединении резисторов(.17б)

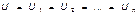а ток I равен сумме всех токов на нагрузках (резисторах):

Общее сопротивление R участка цепи рассчитывается по формуле:

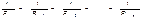Можно сделать вывод, что при последовательном соединении резисторов сопротивление на участке цепи возрастает, а при параллельном - уменьшается.

Соединение конденсаторов.

На рис. 2.18 изображены два способа соединения конденсаторов - последовательное и параллельное.

При последовательном соединении конденсаторов (рис. 2.18а)

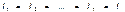
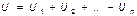
В отличие от резисторов общая ёмкость конденсаторов рассчитывается по формуле:

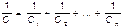
При параллельном соединении конденсаторов (рис. 2.18б).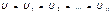

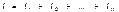
Общая ёмкость рассчитывается следующим образом

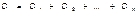Отсюда можно сделать вывод, что если конденсатор последовательно соединить с другим конденсатором, то их общая ёмкость уменьшится, если параллельно - увеличится.

Замена треугольника сопротивлений эквивалентной звездой и наоборот.

Несмотря на то, что эта схема имеет один источник питания, она не поддаётся расчету методом эквивалентных сопротивлений, так как в ней нет сопротивлений, включенных между собой последовательно или параллельно.

Особенностью этой схемы является наличие замкнутых контуров из трёх сопротивлений (R_ab, R_bc, R_ac и R_bd, R_cd, R_bc) причём точки, разделяющие каждую пару смежных сопротивлений, являются узловыми. Такие контуры называются треугольниками сопротивлений.

Воспользуемся способом расчета, который состоит в замене треугольника сопротивлений эквивалентной трёхлучевой звездой сопротивлений (R_a, R_b, R_c ) как показано на рис. 2.19 пунктиром.

Замена треугольника сопротивлений эквивалентной звездой, и наоборот, осуществляется при условии, что такая замена не изменяет потенциалов узловых точек a, b, c, являющихся вершинами треугольника и эквивалентной звезды.

Одновременно предполагается, что в остальной части схемы, незатронутой преобразованием, режим работы не изменяется (не изменяются токи, напряжения, мощности).

Без доказательства приведём формулы, которые служат для определения сопротивлений трёхлучевой звезды по известным сопротивлениям эквивалентного треугольника.

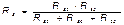
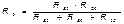
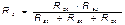
Обратное преобразование трёхлучевой звезды в эквивалентный треугольник, осуществляется