Обратная функция

Пусть задана числовая функция ( ): .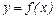

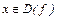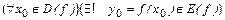Обратная задача: по заданному значению функции у₀ найти соответствующее значение аргумента – решить относительно x уравнение: 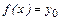, 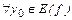. (1)

Если функция f(x) такова, что каждое значение 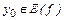, она принимает только при одном значении 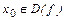, то ее называют обратимой: ( )( .

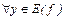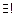
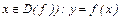Для обратимой функции прямая 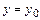( 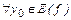) пересечет 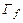в единственной точк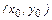е , где 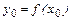. Таким образом можно построить функцию x=g(y), обратную данной. Если перейти к прежним обозначениям (x - аргумент), то функция y=g(x) обратная к данной. Взаимно-обратные функции обладают свойствами:

1) , ;

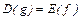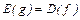2) ;

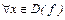
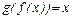3) 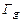симметричен 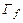относительно прямой y=x.

Теорема. Если функция у=f(x) непрерывна и строго возрастает (строго убывает) на [а;b], то на [А;В], где А= f(a), В= f(b) определена непрерывная строго возрастающая (строго убывающая) обратная функция x=g(y).

gПусть f(x) - строго возрастает: .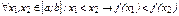

Множество значений непрерывной на отрезке [a,b] функции есть отрезок 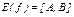, поскольку .

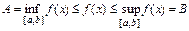Из строгой монотонности имеем, что 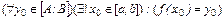. Если бы уравнение 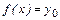имело еще один корень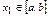 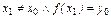(к примеру, 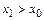), то 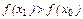. Это противоречит условию: 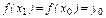. Следовательно, для f на [a,b] существует обратная функция x=g(y), для которой D(g)=[A;B], E(g)=[a;b].

Покажем, что g строго возрастает на [A;B]:

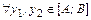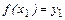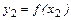: < Þ х₁ < х₂. (2)

если бы было 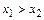, то, в силу строгой монотонности функции f, 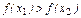. При х₁ = х₂ имели бы 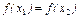. Поэтому справедливо неравенство 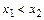, что доказывает монотонность обратной функции.

Докажем непрерывность обратной функции в любой точке 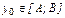. Известно, что этому значению соответствует единственная точка 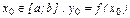или 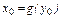. Пусть 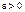(достаточно малое), чтобы 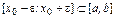и 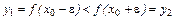. Тогда из строгой монотонности следует, что 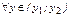соответствующее значение 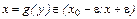. Значит, 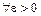можно подобрать окрестность 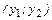точки y₀, такую, что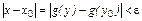 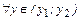. Это подтверждает непрерывность обратной функции в точке y_0.

Для концевой точки 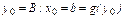считаем: 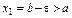, 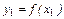. Поэтому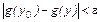 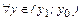.n