Абсолютная и условная сходимость

Ряд 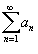называется абсолютно сходящимся, если ряд 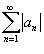также сходится.
Если ряд 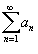сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.
Ряд 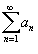называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

26. Функциональные ряды. Степенные ряды. Теорема об области сходимости степенного ряда.

27.Ряды Тейлора. Критерий представимости функции рядом Тейлора.

Ряд Тейлора — разложение функции в бесконечную сумму степенных функций

Пусть функция f(x) бесконечно дифференцируема в некоторой окрестности точки a, тогда ряд

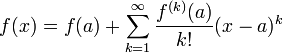
называется рядом Тейлора функции f в точке a.

В случае, если a = 0, этот ряд иногда называется рядом Маклорена.

Если f есть аналитическая функция, то её ряд Тейлора в любой точке a области определения f сходится к f в некоторой окрестности a.