Вероятность безотказной работы

Вариант для контрольных работ

Последняя цифра номера зачетной книжки	Значение параметров для задач
Задача 1	Задача 2	Задача 3
Необходимо найти	P(3000); Q(3000)	α (3500); λ (3500)	P(3000); P(3100); P(3050); α (3050); λ (3050)
	Nо= 1200 n(t)=70	Nо= 1200 n(t)=70 n(Δt)=40	Nо= 600 n(t)= 300 n(Δt)= 100
	Nо= 1000 n(t)=120	Nо= 1000 n(t)=120 n(Δt)=60	Nо= 500 n(t)= 250 n(Δt)= 120
	Nо=800 n(t)=60	Nо=800 n(t)=60 n(Δt)=40	Nо= 800 n(t)= 400 n(Δt)= 200
	Nо= 900 n(t)= 40	Nо= 900 n(t)= 40 n(Δt)=30	Nо= 420 n(t)= 200 n(Δt)= 120
	Nо= 1000 n(t)=90	Nо= 1000 n(t)=90 n(Δt)=70	Nо= 500 n(t)=220 n(Δt)=80
	Nо=1100 n(t)=100	Nо=1100 n(t)=100 n(Δt)=80	Nо= 600 n(t)=340 n(Δt)=100
	Nо=1200 n(t)=120	Nо=1200 n(t)=120 n(Δt)=60	Nо= 700 n(t)= 300 n(Δt)= 140
	Nо= 600 n(t)= 56	Nо= 600 n(t)= 56 n(Δt)=40	Nо= 380 n(t)= 160 n(Δt)= 80
	Nо= 800 n(t)= 44	Nо= 800 n(t)= 44 n(Δt)=30	Nо= 340 n(t)= 120 n(Δt)= 80
	Nо= 1400 n(t)= 110	Nо= 1400 n(t)= 110 n(Δt)=80	Nо= 420 n(t)= 200 n(Δt)= 80

Вероятность безотказной работы

Вероятностью безотказной работы называется вероятность того, что при определенных условиях эксплуатации в заданном интервале времени или в пределах заданной наработки не произойдет ни одного отказа.

Согласно определению 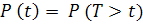, (1.1)

где t – время, в течении которого определяется вероятность безотказной работы; Т – время работы изделия от его первого включения до первого отказа.

Вероятность безотказной работы по статистическим данным об отказах оценивается выражением 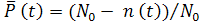, (1.2)

где 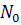- число изделий в начале испытания; n(t) – число отказавших изделий за время t; 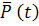- статистическая оценка вероятности безотказной работы. При большом числе изделий 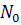статистическая оценка 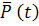практически совпадает с вероятностью безотказной работы 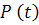. На практике иногда более удобной характеристикой является вероятность отказа Q (t).

Вероятностью отказаназывается вероятность того, что при определенных условиях эксплуатации в заданном интервале времени возникает хотя бы один отказ. Отказ и безотказная работа являются событиями несовместными и противоположными, поэтому

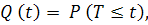
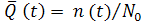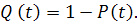, (1.3)

Частотой отказов называется отношение числа отказавших изделий в единицу времени к первоначальному числу испытываемых изделий при условии, что все вышедшие из строя изделия не восстанавливаются.

Согласно определению 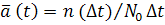, (1.4)

где 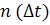- число отказавших образцов в интервале времени

от 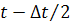до .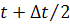

Частота отказов есть плотность вероятности ( или закон распределения ) времени работы изделия до первого отказа. Поэтому

,

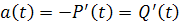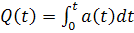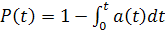, . (1.5)

Интенсивностью отказов называется отношение числа отказавших изделий в единицу времени к среднему числу изделий, исправно работающих в данный отрезок времени.

Согласно определению 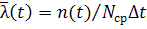. (1.6)

где 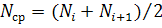– среднее число исправно работающих изделий 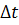; 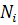- число изделий, исправно работающих в начале интервала ;

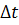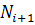- число изделий исправно работающих в конце интервала .

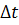Выражение (1.6) есть статистическое определение интенсивности отказов. Вероятностная оценка этой характеристики находится из выражения

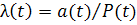. (1.7)

Интенсивность отказов и вероятность безотказной работы связаны между собой зависимостью 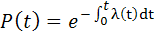. (1.8)

Средней наработкой до первого отказа называется математической ожидание времени работы изделия до отказа.

Как математическое ожидание, 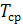вычисляется через частоту отказов (плотность распределения времени безотказной работы) :

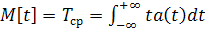. (1.9)

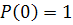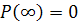Так как t положительно и , а , то

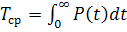. (1.10)

По статистическим данным об отказах средняя наработка до первого отказа вычисляется по формуле 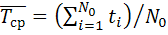, (1.11)

где 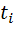- время безотказной работы 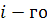образца; 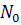– число испытуемых образцов.

Как видно из формулы (1.11), для определения средней наработки до первого отказа необходимо знать моменты выхода из строя всех испытуемых элементов. Поэтому для вычисления 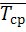пользоваться указанной формулой неудобно. Имея данные о количестве вышедших из строя элементов 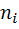в каждом 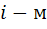интервале времени, среднюю наработку до первого отказа лучше определять из уравнения 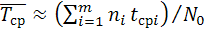. (1.12)

В выражении (1.12) 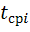и 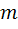находятся по следующим формулам:

; ,

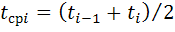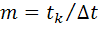где 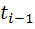- время начала 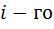интервала; 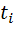- время конца 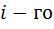интервала; 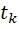– время, в течении которого вышли из строя все элементы;

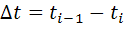– интервал времени.

При изучении надежности технических устройств наиболее часто применяются следующие законы распределения времени безотказной работы: экспоненциальный, усеченный нормальный, Релея, Гамма, Вейбулла, логарифмический – нормальный.