Собственные значения и собственные векторы
Пусть задано линейно преобразование вида
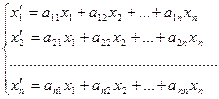 , (1)
, (1)
которое вполне определяется матрицей коэффициентов 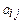
( 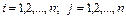 )
)
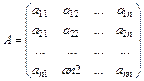 .
.
Матрица А называется матрицей линейного преобразования.
Вектор 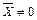 называется собственным вектором линейного преобразования, заданного матрицей А , если найдется такое число λ , что выполняется условие
называется собственным вектором линейного преобразования, заданного матрицей А , если найдется такое число λ , что выполняется условие 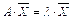 .
.
Это число λ называют собственным значением линейного преобразования, соответствующим собственному вектору 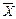 .
.
Каждое собственное значение матрицы А является корнем ее характеристического уравнения
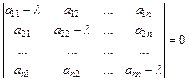 . (2)
. (2)
Координаты собственных векторов, соответствующих найденным собственным значениям, находят из системы уравнений
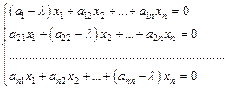 . (3)
. (3)
Пример. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей
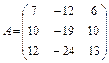 .
. 
Решение. Составляем характеристическое уравнение
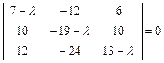 .
.
Раскроем определитель по правилу треугольника
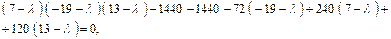
В результате преобразований последнее выражение примет вид:
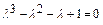 .
.
Разложим левую часть уравнения на множители
 ,
,
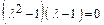 ,
,
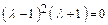 .
.
Решением уравнения 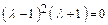 будут значения
будут значения 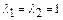 ,
, 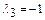 , которые являются собственными значениями матрицы А.
, которые являются собственными значениями матрицы А.
Для отыскания координат собственных векторов составим систему уравнений
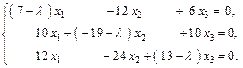
Найдем собственные векторы, соответствующие значению 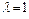 .
.
При 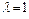 получим систему уравнений
получим систему уравнений
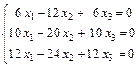 ,
,
или
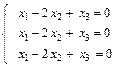 .
.
Легко видеть, что ранг матрицы системы равен 1, и система эквивалентна одному уравнению:
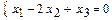 ,
,
откуда
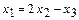 .
.
Если принять 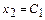 , а
, а 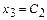 , то значение
, то значение 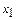 будет равно
будет равно 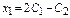 , где
, где 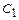 и
и 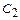 - произвольные действительные числа.
- произвольные действительные числа.
Таким образом, все собственные векторы, соответствующие 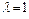 , определяются равенством
, определяются равенством
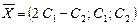 .
.
Найдем собственные векторы, соответствующие 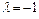 .
.
При 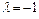 получим систему уравнений
получим систему уравнений
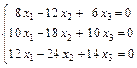
или
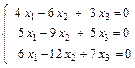 .
.
Запишем матрицу этой системы уравнений
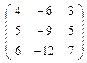 .
.
Так как определитель этой матрицы равен 0, а минор второго порядка
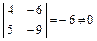 ,
,
то ранг матрицы равен двум, и первые два уравнения системы линейно независимы. Оставим в системе только независимые уравнения, члены с 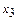 перенесем в правые части уравнений:
перенесем в правые части уравнений:
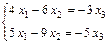 .
.
Пусть 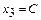 , где
, где 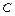 - любое действительное число. Тогда система уравнений примет вид:
- любое действительное число. Тогда система уравнений примет вид:
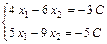 .
.
Решим эту систему методом Гаусса
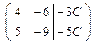 ~
~ 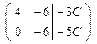 ,
,
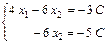 ,
,
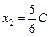 ,
, 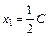 .
.
Таким образом, все собственные векторы, соответствующие 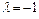 , определяются равенством
, определяются равенством
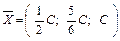
или
 .
.
Ответ.При собственном значении 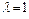 собственные векторы равны
собственные векторы равны 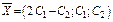 . При собственном значении
. При собственном значении 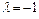 собственные векторы равны
собственные векторы равны  .
.
Задачи для самостоятельного решения
Найти собственные векторы матрицы и соответствующие им собственные значения:
-
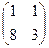 .
. -
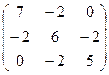 .
. -
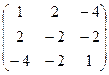 .
.
Ответы: 1) 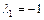 ,
, 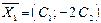 ,
, 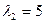 ,
, 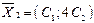 ,
,
2) 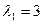 ,
, 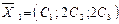 ,
, 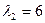
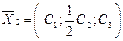
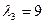
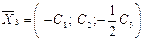 , 3)
, 3) 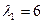 ,
, 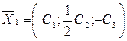 ,
,
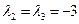
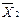 - любой вектор, удовлетворяющий условию
- любой вектор, удовлетворяющий условию 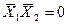 .
.
ОГЛАВЛЕНИЕ
СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Основные понятия и определения
1.2.Методы решения систем линейных уравнений
Метод Крамера
Матричный метод
Метод Гаусса
1.3.Задачи для самостоятельного решения
1.4 Вопросы для подготовки к экзамену
КОМПЛЕКСНЫЕ ЧИСЛА
