Лекция 8. Кривые второго порядка.

Прямая линия описывается общим уравнением 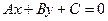, в которое текущие координаты x и y входят с первой степенью. Такие уравнения называются линейными или уравнениями первого порядка. Уравнения кривых (линий) на плоскости, содержащие, кроме первых степеней координат x и y, квадраты этих координат или их произведение xy, относятся к уравнениям кривых второго порядка.

П.1. Окружность. Если R– радиус окружности, а точка M(x₀,y_o) – ее центр, то уравнение окружности имеет вид:

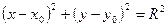. (8.1)

Если точка M совпадает с началом координат, то .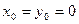

П.2. Эллипс. Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных точек F₁ и F₂ этой плоскости, называемых фокусами эллипса, есть заданная постоянная величина, равная 2a, a>0, большая, чем расстояние между фокусами.

Расстояние между фокусами обозначают 2c. Если за ось Ox принять прямую, проходящую через фокусы F₁ и F₂, а за ось Oy– перпендикуляр к оси Ox в середине отрезка F₁F₂, то простейшее (каноническое) уравнение эллипса примет вид:

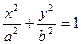, (8.2)

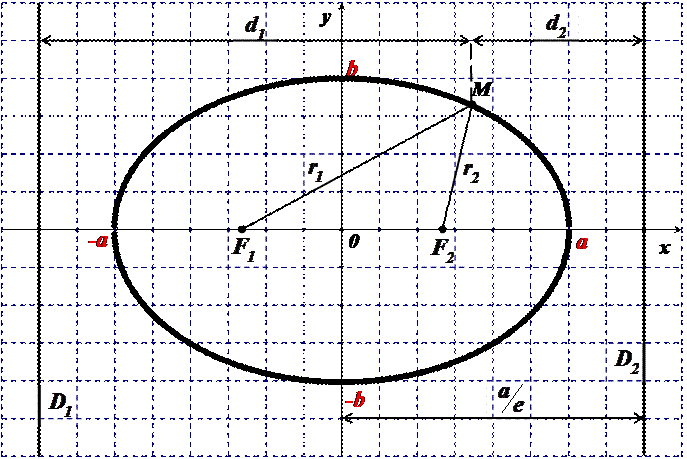
где a– большая полуось эллипса, b– малая полуось, причем 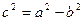(рис. 8.1). Отношение 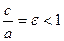называется эксцентриситетом эллипса.

Рис. 8.1

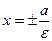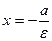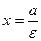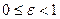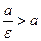При изучении эллипса большую роль играют две прямые: , которые называют директрисами эллипса. Директриса называется левой, а – правой. Так как для эллипса , то , и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая – правее правой вершины.

Директрисы эллипса обладают следующим свойством: отношение расстояния от любой точки эллипса до фокуса к расстоянию 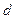от нее до соответствующей директрисы есть величина постоянная, равная эксцентриситету эллипса, т.е. .

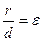Замечание.Если центр эллипса с полуосями a и b смещен в точку M(x₀,y_o), то его каноническое уравнение имеет вид:

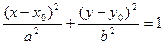. (8.3)

Пример 8.1. Составить каноническое уравнение эллипса, зная, что его большая полуось равна 12, а эксцентриситет равен 0,5. Найти расстояние между фокусами эллипса.

Решение. По условию имеем: a=12, .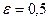

Воспользуемся формулой, выражающей эксцентриситет через отношение полуосе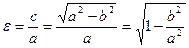й: или 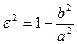, откуда .

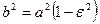Получаем: .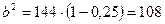

Следовательно, каноническое уравнение эллипса имеет вид: .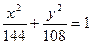

П.3. Гипербола. Гиперболой называется множество точек плоскости, модуль разности расстояний от которых до двух данных точек F₁ и F₂ той же плоскости, называемых фокусами гиперболы, есть заданная постоянная величина 2a, a>0, меньшая, чем расстояние между фокусами. Расстояние между фокусами обозначим 2c.

Если за ось Ox принять прямую, проходящую через фокусы F₁ и F₂, а за ось Oy – перпендикуляр к оси Ox в середине отрезка F₁F₂, то каноническое (простейшее) уравнение гиперболы примет вид

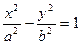, (8.4)

где 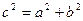, a–действительная полуось, b– мнимая полуось гиперболы (рис. 8.2).

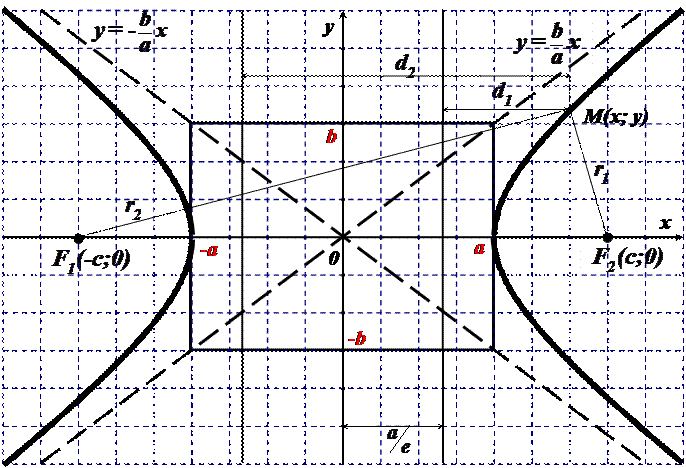
Рис. 8.2

Отношение 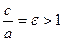называется эксцентриситетом гиперболы. Прямые 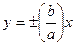называют асимптотами гиперболы. Гипербола, у которой a=b, называется равносторонней. Точки (a,0) и (-a,0) называются вершинами гиперболы.

Для построения гиперболы (8.4) удобно сначала построить прямоугольник со сторонами 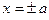, 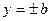и провести через его противоположные вершины асимптоты гиперболы. Тогда гипербола располагается относительно этого прямоугольника так, как изображено на рисунке 8.2.

Прямые, заданные уравнениями 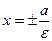, называются директрисамигиперболы. Как и для эллипса, отношение расстояния r_i от любой точки гиперболы до фокуса F_i к расстоянию d_i от этой точки до соответствующей этому фокусу директрисы D_i равно эксцентриситету гиперболы, т.е: , .

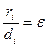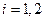Замечания. 1) Кривая 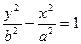также является гиперболой. Здесь Oy – действительная ось, Ox – мнимая ось, вершины гиперболы расположены на оси Oy.

2) Если центр гиперболы смещен в точку M(x₀,y_o), то ее каноническое уравнение имеет вид

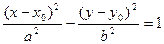или 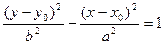. (8.5)

Пример 8.2. Асимптоты гиперболы имеют уравнения 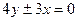, а расстояние между фокусами равно 20. Написать ее каноническое уравнение.

Решение. Разрешим уравнения асимптот относительно y и, сравнив с общей формулой асимптот, найдем отношение b к a:

.

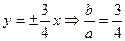По условию задачи 2с=20, т. е. с=10. Так как для гиперболы 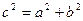, то для нахождения a и b получим систему уравнений

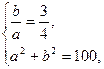
решив которую, найдем a=8, b=6.

Следовательно, каноническое уравнение гиперболы имеет вид: 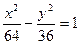.