Решение линейной задачи расчета ЭМП в пазу электрической машины при протекании синусоидального тока по проводнику прямоугольного сечения, расположенном в пазу

При прохождении тока по проводнику, расположенному в пазу электрической машины (рис. 1), силовые линии магнитного поля частично замыкаются по магнитопроводу, а частично по проводнику и изоляции. Большая часть силовых линий проходит по участкам магнитной цепи, занятых сталью, откуда силовые линии выходят в паз электрической машины под прямым углом по отношению к боковой поверхности паза. Причиной такого распределения магнитного поля является то обстоятельство, что при изготовлении паза используется электротехническая сталь, которая имеет магнитную проницаемость много больше магнитной проницаемости проводника, расположенного в пазу. При наличии шихтованного магнитопровода проводимость изоляции между стальными листами близка к нулю.

При описании поверхностного эффекта в пазу электрической машины примем следующие допущения [1]:

· магнитная проницаемость стали зубцов бесконечно велика;

· магнитное поле в пазу перпендикулярно боковым стенкам и параллельно дну паза;

· сердечник магнитопровода изготовлен из тонких изолированных друг от друга пластин и вихревые токи в сердечнике отсутствуют;

· температура проводника во всех точках сечения проводника одинакова.

Рис. 1. Картина магнитного поля в ферромагнитном пазу

Применяя уравнения Максвелла к рассматриваемой задаче, получим:

rot ; (1)

rot (2)

где - вектор напряженности магнитного поля; - вектор напряженности электрического поля; - удельная проводимость проводника; - магнитная проницаемость проводника; - относительная магнитная проницаемость проводника; - магнитная постоянная, равная Гн/м.

Перейдем от системы уравнений (1) и (2) с двумя неизвестными и к одному уравнению с одним неизвестным или . Для этого возьмем ротор от обеих частей первого равенства

rot (rot ) = ( rot ) . (3)

Выполнив подстановку выражения rot из уравнения (2) в уравнение (3), получим:

rot (rot ) = . (4)

С другой стороны

rot (rot ) = (5)

где - оператор «набла».

Так как внутри проводника нет объемных зарядов, то и значит

rot (rot ) = (6)

Следовательно, дифференциальное уравнение электрического поля и аналогичное уравнение магнитного поля можно записать в виде:

(7)

(8)

В уравнениях (7) и (8) векторы напряженности и поля являются синусоидальными функциями, изменяющимися с частотой , так как характеризуют переменное поле, созданное синусоидальным током той же частоты в проводнике, расположенном в ферромагнитном пазу. В комплексной форме записи векторы напряженности имеют вид:

; (9)

где и - комплексные амплитуды напряженностей электрического и магнитного поля.

Подставляя выражения (9) в уравнения (7) и (8) и сокращая затем на множитель , получим уравнения для комплексных амплитуд напряженностей электрического и магнитного полей

(10)

(11)

При малой ширине паза и при небольшой толщине изоляции в сравнении с толщиной проводника во всех точках внутри проводника за исключением открытого конца паза вектор напряженности магнитного поля имеет только x - составляющую (рис. 1). Вектор плотности тока направлен вдоль оси z параллельно граничной поверхности. Вектор напряженности электрического поля имеет только z - составляющую, то есть . При этом напряженность электрического поля зависит только от расстояния (переменной y) рассматриваемой точки проводника от его поверхности, но не зависит от переменных и . Поэтому уравнение (10) можно записать иначе

(12)

Общее решение уравнения (12) будет

(13)

Здесь обозначено

; . (14)

Величина, обратная коэффициенту , есть глубина проникновения электромагнитного поля в ферромагнитный паз, отсчитываемая по высоте проводника

. (15)

Таким образом

(16)

Аналогично (16) можно определить общее решение уравнения для комплексной амплитуды напряженности магнитного поля. Принимая во внимание, что , запишем уравнение (11) в виде

(17)

Тогда общее решение уравнения (17) будет

(18)

где и - постоянные интегрирования.

При определении постоянных интегрирования целесообразно выразить одно из общих решений (16) или (18) соответственно для напряженностей электрического или магнитного поля через другое, воспользовавшись уравнениями Максвелла. Подставляя общее решение (18) для напряженности магнитного поля в уравнение (1), получим

(19)

где .

Остается определить коэффициенты и , исходя из граничных условий и .

На дне паза напряженность магнитного поля , то есть

(20)

Действительно, при конечном значении тока магнитный поток, охватывающий проводник в открытом пазу, должен быть конечным. Но если магнитный поток конечен, а магнитная проницаемость электротехнической стали, из которой изготовлен ферромагнитный паз, является бесконечно большой, то напряженность магнитного поля в ней будет равна нулю. Кроме того, на границе раздела сред с различными магнитными проницаемостями касательная составляющая напряженности магнитного поля не претерпевает разрыв (не меняется скачком).

На открытом конце паза , исходя из закона полного тока, получим:

(21)

где комплексная амплитуда напряженности магнитного поля на поверхности паза; - ширина паза.

Действительно, выбрав контур, идущий от левой стенки паза к правой стенке между проводником, и дальше замыкающийся по ферромагнетику (пренебрегая падением магнитного напряжения в сердечнике), получим

(22)

Для определения коэффициентов и объединим уравнения (20) и (21) в систему. Из решения системы уравнений находим:

(23)

Подставляя выражения , из (23) в (18) и (19), получим:

; (24)

(25)

Плотность тока в сечении проводника, расположенном в ферромагнитном пазу, из закона Ома будет:

(26)

Выражения (24) и (25) для комплексных амплитуд напряженностей магнитного и электрического поля отражают типичные особенности распространения плоских волн в проводящую среду: результирующее поле представляет сумму двух встречно бегущих волн с фазовыми скоростями

(27)

Внизу паза магнитное поле равно нулю. Это значит, что на дне паза поля двух встречных волн равны и противоположны.

Если глубина паза существенно больше глубины проникновения электромагнитной волны в проводнике, заполняющем паз, то отраженной волной можно пренебречь и формулы (24) и (25) примут более простой вид:

(28)

. (29)

Распространяясь вглубь проводника, волна затухает в нем, так как по пути распространения часть электромагнитной энергии переходит в тепловую энергию.

Неравномерность распределения тока по сечению проводника приводит к увеличению его сопротивления.

Комплексное сопротивление проводника определяется соотношением

(30)

где - комплексная мощность, поглощаемая в проводнике, 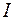- действующее значение тока в проводнике.

Комплексная мощность , входящая в проводник, определяется потоком комплексного вектора Пойтинга через поверхность проводника. Этот поток отличен от нуля только на открытой части паза :

(31)

Выражение показывает, что комплексная мощность проводника определяется произведением комплекса напряжения у поверхности проводника на сопряженный комплекс тока.

Комплексное сопротивление проводника в ферромагнитном пазу будет:

(32)

где , - соответственно активная и реактивная составляющие полного сопротивления проводника, - длина проводника, b – ширина проводника.

Выполнив подстановку выражений (24) и (25) в (32), задавшись в них значением , получим:

(33)

В формуле (33) принято, что толщина проводника мало отличается от ширины паза.

Сравним сопротивления проводника в пазу на переменном и постоянном токе. На постоянном токе, вследствие равномерного распределения тока, сопротивление проводника в пазу

. (34)

Преобразуем выражение (33), воспользовавшись выражениями (34) и (15), тогда получим

(35)

Рассмотрим числовой пример с исходными данными: , , , , .

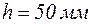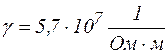После расчета получим:

,

,

.

Отсюда следует

Из расчета видно, что на переменном токе за счет поверхностного эффекта возрастает активная составляющая полного сопротивления проводника, изменяется его индуктивное сопротивление. По данным расчета, например при токе , тепловые потери на постоянном токе составляют , а на переменном токе увеличиваются более чем в три раза . Таким образом, поверхностный эффект вызывает дополнительный нагрев обмоток электрических машин.