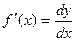Теоремы о непрерывных функциях. Непрерывность на отрезке. Равномерная непрерывность.

Теорема: f(x) и g(x) непрерывны в т.х0, то:

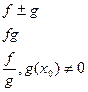- непрерывны в точке х0.

Доказательство: : 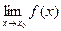=f(x0).

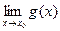: =g(x0).

.

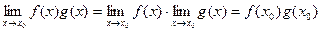Следствие 1: любой многочлен является непрерывной функцией любой точки действительной оси.

Следствие 2: любая рациональная функция: 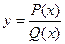такая, что 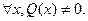(это значит, что любая рациональная функция может иметь не более чем конечное число т.р.2).

Теорема:( о существовании обратной функции):

если функция y=f(x) непрерывна и строго монотонна на [a,b] оси Ох, то обратная функция 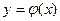также непрерывна и монотонна на соответствующем отрезке [c,d] оси Оу.

Свойства функций, непрерывных на отрезке:

Теорема (Вейерштрасса): если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.

Следствие: если функция непрерывна на отрезке, то она ограничена на этом отрезке.

Непрерывность функции в интервале и на отрезке:

Функция y=f(x) называется непрерывной в интервале (a,b),если она непрерывна в каждой точке этого интервала.

Функция y=f(x) называется непрерывной на отрезке [a,b] , если она непрерывна в интервале (a,b) и в точке х=а непрерывна справа (т.е. 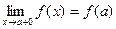), а в точке x=b непрерывна слева ( ).

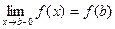Равномерная непрерывность:

Функция f: X → R называется равномерно-непрерывной на множестве X, если

.

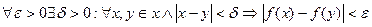Производная функции, ее геометрический и физический смысл.

Определение. Производной функции f(x) в точке х = х₀ называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.

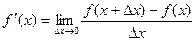
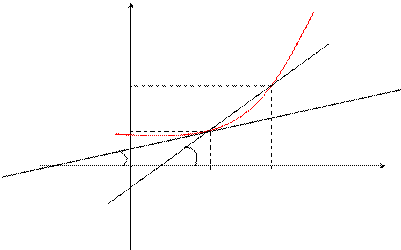
у

f(x)

f(x₀ +Dx) P

Df

f(x₀) M

a b x 0 x₀ Dx x₀ + Dx

Пусть f(x) определена на некотором промежутке (a, b). Тогда 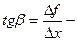тангенс угла наклона секущей МР к графику функции.

,

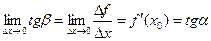где a - угол наклона касательной к графику функции f(x) в точке (x₀, f(x₀)).

Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.

Уравнение касательной к кривой:

Уравнение нормали к кривой: .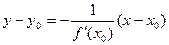

Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.

Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.

Соответственно, вторая производная функции- скорость изменения скорости, т.е. ускорение.

Дифференциал функции.

Пусть функция y = f(x) имеет производную в точке х: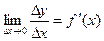

Тогда можно записать: 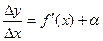, где a®0, при Dх®0.

Следовательно: .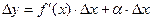

Величина aDx- бесконечно малая более высокого порядка, чем f¢(x)Dx, т.е. f¢(x)Dx- главная часть приращения Dу.

Определение. Дифференциалом функции f(x) в точке х называется главня линейная часть приращения функции.

Обозначается dy или df(x).

Из определения следует, что dy = f¢(x)Dx или dy = f¢(x)dx.

Можно также записать: