Скалярным произведением двух векторов называется действительное число, равное произведению длин умножаемых векторов на косинус угла между ними.

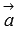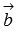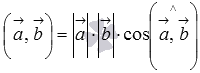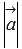Скалярное произведение векторов и будем обозначать как . Тогда формула для вычисления скалярного произведения имеет вид , где и 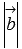- длины векторов 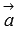и 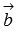соответственно, а 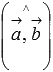- угол между векторам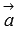и и .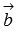

Из определения скалярного произведения видно, что если хотя бы один из умножаемых векторов нулевой, то .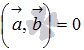

Вектор можно скалярно умножить на себя. Скалярное произведение вектора на себя равно квадрату его длины, так как по определению .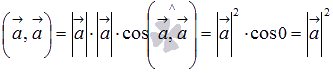

Угол между векторами — угол между направлениями этих векторов (наименьший угол).

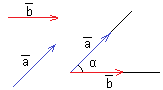
По определению, угол между двумя векторами находится в промежутке [0°; 180°].
Угол между векторами 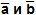обозначается так: .
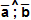Если векторы перпендикулярны, то угол между ними равен 90º. Если векторы сонаправлены, в частности один из них или оба нулевые, то угол между ними равен 0^о. Если противоположно направленные векторы, то угол между ними равен 180º.
Угол между двумя ненулевыми векторами находится с помощью вычисления скалярного произведения. По определению скалярное произведение равно произведению длин векторов на косинус угла между ними (скалярное произведение для двух векторов с координатами (x₁; y₁) и (x₂; y₂) вычисляется по формуле: x₁x₂ + y₁y₂).

15. N-мерным вектором называется последовательность 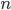чисел. Эти числа называются координатами вектора. Число координат вектора n называется размерностью вектора.

Линейной комбинацией векторов 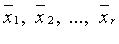называют вектор

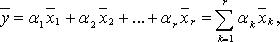
где 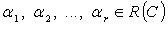- коэффициенты линейной комбинации. Если 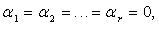комбинация называется тривиальной, если 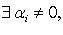- нетривиальной.

Система 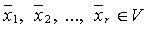линейно зависима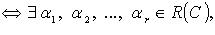 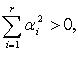что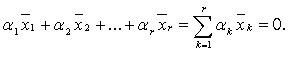

Система 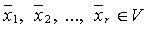линейно независима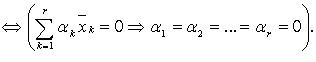

16. Векторное (линейное) пространство — это математическая структура, которая формируется набором элементов, называемых векторами, для которых определены операции сложения друг с другом и умножения на число — скаляр.

Размерностью векторного пространства называется число, равное максимальному количеству линейно независимых векторов в этом пространстве.

Базис векторного пространства – это упорядоченная совокупность линейно независимых векторов этого пространства, число которых равно размерности пространства.

17. Скалярным квадратом n-мерного вектора 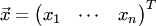называется скалярное произведение вектора на себя:

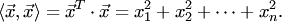
Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность 3.

В современном понимании, в более общем смысле, может обозначать один из сходных и тесно связанных объектов, определённых ниже. Обычно 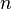-мерное евклидово пространство обозначается 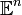, хотя часто используется не вполне приемлемое обозначение .

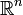Норма в векторном пространстве 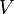над полем вещественных или комплексных чисел — это функционал 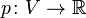, обладающий следующими свойствами:

1.

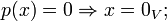
2. 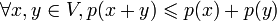(неравенство треугольника);

3.

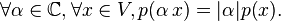
Эти условия являются аксиомами нормы.

18. Условия ортогональности векторов. Два вектора a и b

ортогональны (перпендикулярны), если их скалярное произведение равно нулю

a· b= 0

Так в случае плоской задачи вектора a= {a_x;a_y}и b= {b_x; b_y} ортогональны, если a· b = a_x · b_x + a_y · b_y = 0

Базис e₁, e₂, … , e_n в n –мерном евклидовом пространстве E_n называется ортогональным, если (e_i, e_j) = 0 i ≠ j , т.е. все векторы попарно ортогональны.

Ортогональный базис из единичных векторов называется ортонормированным.

19. Оператором называется правило, по которому каждому элементу x некоторого непустого множества X ставится в соответствие единственный элемент y некоторого непустого множества Y. Говорят, что оператор действует из X в Y.

Действие оператора обозначают y = A(x), y — образ x, x — прообраз y.

Если каждый элемнт y из Y имеет единственный прообраз x из X, y= A(x), оператор называют взаимно однозначным отображением X в Y или преобразованием X, X — область определения оператора.

Пусть X и Y два линейные пространства. Оператор A, действующий из X в Y, называется линейным оператором, если для любых двух элементов uи v из X и любого числа α справедливо:

A(u+ v) = A(u) + A(v) , A(α·u) = α· A(u).

Если элементу x соответствует y, то y называется образом элемента x, а x - прообразом элемента y. Пишут: 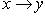или y = f(x). Множество Aвсех элементов 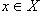, имеющих один и тот же образ 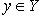, называется полным прообразом элемента y.

20. Матрицей линейного оператора в базисах e, f называется матрица A, столбцами которой являются координаты образов базисных векторов базиса e в базисе f , A = {a_ij}= {A(e_j )_i}:

Координаты образа y = A(x) и прообраза x связаны соотношеннием:

y =A· x,

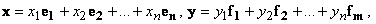
21. Наиболее просто устроены матрицы диагонального вида . Возникает вопрос, нельзя ли найти базис, в котором матрица линейного оператора имела бы диагональный вид. Такой базис существует.

Пусть дано линейное пространство R_n и действующий в нем линейный оператор A; в этом случае оператор A переводит R_n в себя, то есть A:R_n → R_n.

Определение. Ненулевой вектор 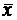называется собственным вектором оператора A, если оператор A переводит 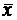в коллинеарный ему вектор, то есть 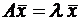. Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору .

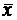Отметим некоторые свойства собственных чисел и собственных векторов.

1. Любая линейная комбинация собственных векторов 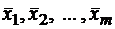оператора A, отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.

2. Собственные векторы 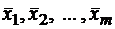оператора A с попарно различными собственными числами λ₁, λ₂, …, λ_mлинейно независимы.

3. Если собственные числа λ₁=λ₂= λ_m= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.

Итак, если имеется 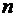линейно независимых собственных векторов 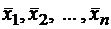, соответствующих различным собственным числам λ₁, λ₂, …, λ_n, то они линейно независимы, следовательно, их можно принять за базис пространства R_n. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 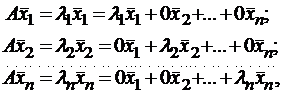тогда .

Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.

Характеристическим многочленом оператора 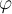называется многочлен 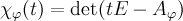.Характеристический многочлен линейного оператора 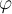не зависит от выбора базиса, в котором представлена его матрица. Уравнение 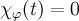называется характеристическим уравнением оператора .

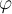22. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 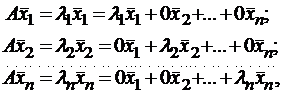тогда .

Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.

23. Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора. Матрица квадратичной формы в произвольном базисе совпадает с матрицей полярной ей билинейной формы в том же базисе..

Матрицу 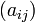называют матрицей квадратичной формы в данном базисе. В случае, если характеристика поля 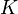не равна 2, можно считать, что матрица квадратичной формы симметрична, то есть .

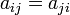Если матрица квадратичной формы имеет полный ранг, то квадратичную форму называют невырожденной, иначе — вырожденной

24. Квадратичная форма называется канонической, если вс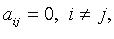е т. е.

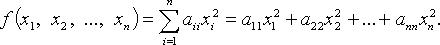
Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований