Решение двух основных задач теории ошибок. Оценка истинного значения измеряемой величины и оценка точности прибора в случае прямых равноточных измерений.

Пусть х₁, х₂, … , х_n, - результаты n прямых независимых измерений некоторой постоянной величины а. Предположим, что возможные результаты всех измерений – случайные величины x₁, x₂, … , x_n подчиняются нормальному закону распределения с одним и тем же центром

Мx_k,=а (k=1, 2, … , n) (3)

(условие несмещенности) и одной и той же дисперсией

М(x_k - а)²=s² (k=1, 2, … , n) (4)

(условие равноточности измерений).

В качестве приближенного значения а принимается среднее арифметическое значение из результатов измерений:

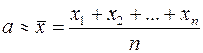(5)

Первой задачей является оценка точности приближенного равенства (5).

Поскольку все случайные величины x_k независимы и имеют нормальное распределение вероятностей с центром а и дисперсией s², средняя случайная величина

,

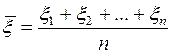как следует из теоремы сложения дисперсий, также имеет нормальное распределение с центром а, но с дисперсией 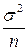. Поэтому вероятность того, что средняя ошибка 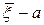не превзойдет по абсолютной величине некоторого положительного числа e , равна

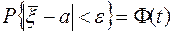, (6)

где

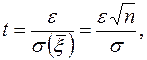
а F(t) есть интеграл вероятностей.

Обычно вероятность оценки (Р) задается заранее и выбирается достаточно близкой к 1 (например Р=0,999). Далее, из уравнения F(t)=Р находится соответствующее значение t (по таблице интеграла вероятностей; например, при Р=0,999 находим t=3,291). Это приводит к оценк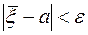е , где 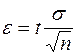. Подставляя в эту оценку вместо случайных величин x_k их опытные значения x_k и, значит, вместо средней 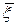ее опытное значение 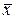, получим так называемую классическую оценку:

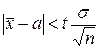
или

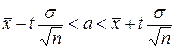(7)

Оценку (7) надо понимать следующим образом: вероятность того, что интервал 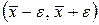, где 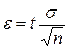, будет заключать истинное значение а измеряемой величины, равна заранее заданному числу Р=F(t). Число Р называется надежностью оценки (7).

Классическая оценка (7) имеет тот существенный недостаток, что при этом предполагается известной дисперсия s². Если же эту дисперсию заменить ее приближенным значением

,

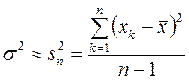то надежность оценки (7) уменьшится. Но оказывается, что и при неизвестной дисперсии s² можно дать точную оценку приближенного равенства 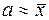, если исходить не из распределения величины 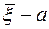, которое зависит от s², а из распределения другой случайной величины

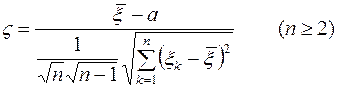
Если x_k (k=1, 2, … , n) независимы и имеют одно и то же нормальное распределение вероятностей с центром в а, то случайная величина z имеет распределение, называемое распределением Стьюдента, с плотностью

,

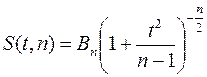где

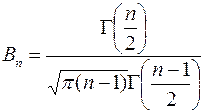
(G - функция Эйлера)

Таким образом, вероятность неравенства |z| < t равна

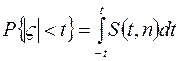
Имея таблицы этого интеграла, можно по заданной вероятности Р найти соответствующее значение t=t(P,n), удовлетворяющее уравнению 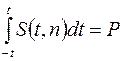. При этом неравенство |z| < t будет иметь заданную вероятность Р.

Переходя снова к опытным значениям x_k величины x_k и учитывая, что выборочная дисперсия равна

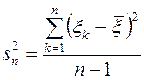
Получаем искомую оценку

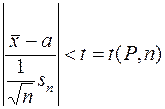
или

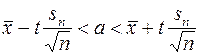(8)

С надежностью Р.

Ниже приводится таблица значений t=t(P,n) для различных значений количества измерений n и обычно задаваемых значений надежности Р.

Таблица 1

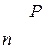	0,95	0,99	0,999		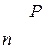0,95	0,99	0,999
	2,78	4,60	8,61		2,093	2,861	3,883
	2,57	4,03	6,86		2,064	2,797	3,745
	2,45	3,71	5,96		2,045	2,756	3,659
	2,37	3,50	5,41		2,032	2,729	3,600
	2,31	3,36	5,04		2,023	2,708	3,558
	2,26	3,25	4,78		2,016	2,692	3,527
	2,23	3,17	4,59		2,009	2,679	3,502
	2,20	3,11	4,44		2,001	2,662	3,464
	2,18	3,06	4,32		1,996	2,649	3,439
	2,16	3,01	4,22		1,991	2,640	3,418
	2,15	2,98	4,14		1,987	2,633	3,403
	2,13	2,95	4,07		1,984	2,627	3,392
	2,12	2,92	4,02		1,980	2,617	3,374
	2,11	2,90	3,97	¥	1,960	2,576	3,291
	2,10	2,88	3,92

В последней строке таблицы (при n=¥) даются значения, совпадающие с соответствующими значениями из таблицы интеграла вероятностей:

Ф(1,960)=0,95; Ф(2,567)=0,99; Ф(3,291)=0,999

Объясняется это тем, что при n®¥ распределение Стъюдента стремится к нормальному распределению, как видно из предельного соотношения

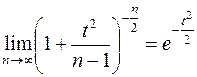
Расчет средних

Для применения оценки (8) требуется по результатам измерений вычислить среднее значение 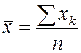и выборочный стандарт

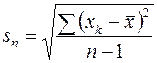
Непосредственный расчет 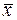и s_n по указанным формулам можно упростить с помощью подходящего линейного преобразования результатов измерения:

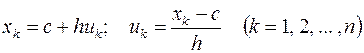(9)

За начало отсчета выбирается некоторое среднее значение между наименьшим и наибольшим значениями x_k; единицу масштаба h выбирают так, чтобы значения u_k выражались целыми числами (что всегда возможно, так как результаты измерения округляются до определенного разряда, связанного с единицей шкалы прибора). Произведя замену (9), мы получаем следующие расчетные формулы:

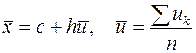(10)

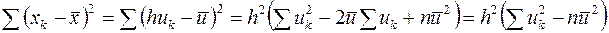
и, значит,

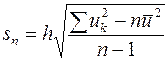(11)

Пример 1:

Таблица

4,781	4,775	4,764	4,780
4,795	4,772	4,776	4,764
4,769	4,791	4,771	4,774
4,792	4,782	4,789	4,778
4,779	4,767	4,772	4,791

дает результаты произведенных Милликеном первых 20 измерений заряда электрона в 10^-10 эл.-ст. единиц. Для обработки этих результатов составим расчетную таблицу, выбрав начало отсчета с = 4,780 и единицу масштаба р=0.001 (при этом для удобства расчета располагаем результаты измерений в порядке их возрастания). Для расчета нам нужны два столбца – столбец приведенных отклонений (u) и столбец их квадратов (u²).

Таблица 2

x		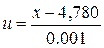u2
4,764	-16
4,764	-16
4,767	-13
4,769	-11
4,771	-9
4,772	-8
4,772	-8
4,774	-6
4,775	-5
4,776	-4
4,778	-2
4,779	-1
4,781
4,782
4,789
4,789
4,791
4,791
4,792
4,795
Суммы	-29

Сумма чисел каждого столбца указанного в последней строке

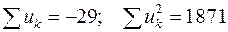
Применяя формулы (10) и (11) получим

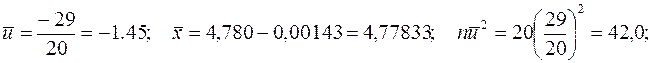
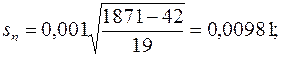
Истинный заряд электрона е, выраженный в 10^-10 эл.-ст. единиц, можно считать приближенно равным

е » 4,7786

Оценим это приближенное равенство, задаваясь надежностью вывода Р=0,99. По таблице на стр. 122 для Р=0,99 и n=20 находим t=2,861. Следовательно, с надежностью вывода Р=0,99 можно утверждать, что истинный заряд заключен между пределами

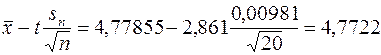
и

,

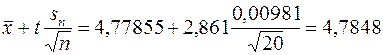То есть что

4,7722 < е < 4,7848 (P = 0,99)

Если увеличить надежность вывода до P = 0,999, то соответствующее значение t увеличится до 3,883 и, следовательно, увеличится интервал для е:

4,7700 < е < 4,7870 (P = 0,999)

Для уменьшения этого интервала надо увеличить число измерений или повысить их точность.

Оценка точности прибора

(точность измерений)

Точность измерений характеризуется величиной s - стандартом распределения случайных ошибок измерения.

Приближенным значением s является выборочный стандарт:

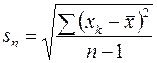
Для оценки приближенного равенства s » s_n можно воспользоваться тем, что распределение вероятностей случайной величины

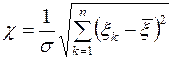
Зависит только от n и не зависит ни от а, ни от s. Если все x_k (k=1, 2, … , n) независимы и имеют одно и то же нормальное распределение с центром а и и дисперсией s², то распределение величины c имеет плотность

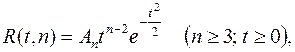
где

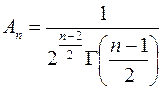
(G - функция Эйлера). Таким образом, вероятность неравенства t₁ < c < t₂ равна

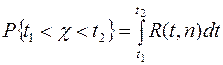(12)

Интеграл (12) позволяет найти вероятность рассматриваемого неравенства 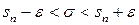, которое записывают в виде

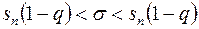, (13)

обозначая через q=e/s_n относительную ошибку.

Действительно, преобразуем неравенство

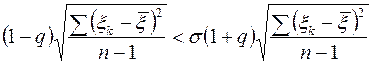(14)

в равносильное, и потому равновероятное ему неравенство

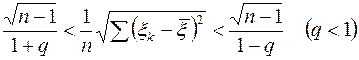
Последнее неравенство имеет вид t₁< c < t₂, этому его вероятность равна интегралу (12), где

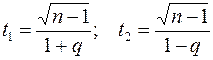
Задаваясь теперь определенной вероятностью Р (надежность оценки), мы можем найти соответствующее значение q=q(P,n) из уравнения

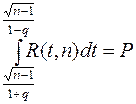
и тогда неравенство (14) будет иметь заданную вероятность Р. Переходя к опытным значениям x_k случайных величин x_k, получаем оценку (13) с заданной надежностью Р.

Замечание. Если q > 1, то ввиду положительности стандарта s неравенство (14) примет вид

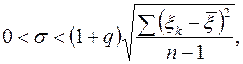
Что равносильно неравенству

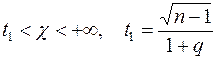
Вероятность Р этого неравенства равна

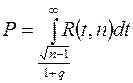
Из этого соотношения и находится q=q(P,n) в случае q > 1. Следовательно, при q > 1 оценка (13) принимает вид

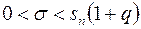
Ниже приводится таблица значений q=q(P,n) для различного количества измерений и обычно задаваемых значений надежности Р.

Таблица 3

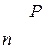	0,95	0,99	0,999		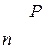0,95	0,99	0,999
	1,37	2,67	5,64		0,37	0,58	0,88
	1,09	2,01	3,88		0,32	0,49	0,37
	0,92	1,62	2,98		0,28	0,43	0,63
	0,80	1,38	2,42		0,26	0,38	0,56
	0,71	1,20	2,06		0,24	0,35	0,50
	0,65	1,08	1,80		0,22	0,32	0,46
	0,59	0,98	1,60		0,21	0,30	0,43
	0,55	0,90	1,45		0,188	0,269	0,38
	0,52	0,83	1,33		0,174	0,245	0,34
	0,48	0,78	1,23		0,161	0,226	0,31
	0,46	0,73	1,15		0,151	0,211	0,29
	0,44	0,70	1,07		0,143	0,198	0,27
	0,42	0,66	1,01		0,115	0,160	0,221
	0,40	0,63	0,96		0,099	0,136	0,185
	0,39	0,60	0,92		0,089	0,120	0,162

Пример 2:

Для рассмотренных выше результатов 20 измерений заряда электрона уже было вычислено значение s_n= 0,00981. Поэтому точность рассматриваемых измерений характеризуется стандартом:

s » 0,00981.

Оценим это приближенное равенство с надежностью Р=0,99. Согласно приведенной таблице 3 при n=20 и Р=0,99 находим q=0,58. Поэтому можно утверждать с надежностью Р=0,99, что стандарт ошибки измерения заключается между числами

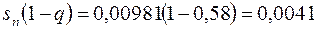
и

,

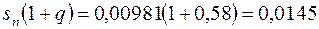т. е. что

0,0041 < s <0,0145 (Р=0,99)

Если надежность метода увеличить до Р=0,999, то соответствующее значение q увеличится до 0,88 и, следовательно, увеличится интервал для s:

0,0012 < s <0,0185 (Р=0,999)

Для уменьшения этого интервала надо значительно увеличить число измерений. Например, для нахождения стандарта s с относительной точностью до 10% надо произвести 350 измерений при Р=0,99 и даже 600 измерений при Р=0,999.

Пример 3:

Оценить с надежностью Р=0,999 истинное значение е заряда электрона по результатам 58 измерений Милликена, приведенным в следующей таблице (все данные в 10^-10 абс. эл.-ст. единиц:

4,781	4,764	4,777	4,809	4,761	4,769
4,795	4,776	4,765	4,790	4,792	4,806
4,769	4,771	4,785	4,779	4,758	4,779
4,792	4,789	4,805	4,788	4,464	4,785
4,779	4,772	4.768	4,772	4,810	4,790
4,775	4,789	4,801	4,791	4,799	4,777
4,772	4,764	4,785	4,788	4,799	4,749
4,791	4,774	4,783	4,783	4,797	4,781
4,782	4,778	4,808	4,740	4,790
4,767	4,791	4,771	4,775	4,747

Средний результат измерений

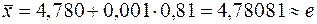
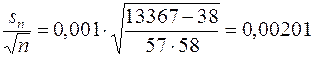
Оценка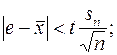

t=t(0,999, 58) = 3,470;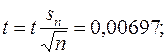

4,7738 < e < 4,7878

Упрощенные оценки, «правило трех сигма»

Оценки рассмотренного выше типа требуют информации о специальных законах распределения вероятностей (распределение Стьюдента, c-распределения и т. п.). Существуют также упрощенные оценки, например «правило трех сигма». Это правило заключается в том, что ошибка приближенного равенства 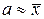не превосходит утроенной средней квадратической ошибки средней 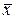. Если величина s известна, то «правило трех сигма»

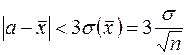
имеет надежность Р = Ф(3)=0,997, как видно из оценки (7). Но «правило трех сигма» применяют и при неизвестной s, заменяя ее приближенным значением s_n. «Правило трех сигма» принимает вид

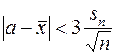(15)

и его надежность оказывается значительно меньшей, чем 0,997, причем эта надежность уменьшается с уменьшением числа измерений n.

Действительно, сравнивая оценку (15) с оценкой (8), замечаем, что при 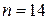оценка (15) имеет надежность, меньшую, чем 0,99, т. к. 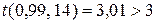; а при 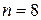надежность оценки (15) становится равной 0,98.

Рассмотрим применение «правила трех сигма» для оценки стандарта ошибки измерения. Можно подсчитать, что средняя квадратическая ошибка выборочного стандарта приближенно равна

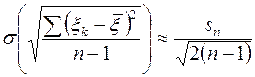
Поэтому «правило трех сигма» принимает вид

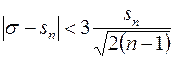(16)

Сравнение этой оценки с оценкой (13) показывает, что даже при 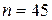оценка (16) имеет надежность, меньшую, чем 0,99, т. к.

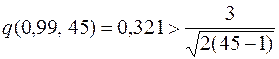
При 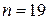оценка (16) имеет надежность 0,98, а при 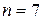надежность становится меньше, чем 0,95.

Пример 4:

Оценить с помощью «правила трех сигма» точность измерений по следующим данным десяти серий измерений одним и тем же прибором различных величин:

1-я серия	2-я серия	3-я серия	4-я серия	5-я серия	6-я серия	7-я серия	8-я серия	9-я серия	10-я серия
4,16	6,04	5,71	4,94	4,50	3,84	5,56	5,33	7,89	4,23
4,19	6,05	5,71	4,92	4,48	3,84	5,54	5,32	7,88	4,21
4,15	6,06	5,70	4,93	4,51	3,83	5,56	5,31	7,89	4,22
4,17	6,03	5,71	4,95	4,49	3,84	5,56	5,34	7,87	4,20
4,18	6,05	5,69	4,94	4,52	3,82	5,55	5,32	7,90	4,22
4,17	6,05	5,71	4,93	4,50	3,84	5,57	5,33	7,89	4,21
4,17	6,05	5,71	4,94	4,50	3,85	5,56	5,32	7,91	4,20
4,16	6,06	5,69	4,94	4,50	3,84	5,55	5,35	7,88	4,21
4,17	6,05	5,71	4,93	4,49	3,84	5,56	5,33	7,89	4,22
4,17	6,04	5,73	4,95	4,50	3,86	5,56	5,34	7,90	4,21
4,17	6,05	5,71	4,96	4,49	3,83	5,57	5,33	7,89	4,21
4,16	6,05	5,72	4,94	4,50	3,84	5,56	5,34	7,90	4,19
4,17	6,07	5,72	4,95	4,50	3,83	5,58	5,33	7,89	4,21
4,18	6,06	5,70	4,93	4,51	3,85	5,56	5,34	7,91	4,22
4,17	6,05	5,71	4,94	4,49	3,82	5,58	5,33	7,89	4,21

При расчете каждой выборочной дисперсии можно учитывать частоту результатов измерения, например, для обработки первой серии измерений можно составить следующую расчетную таблицу:

x	m		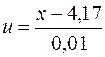mu	mu2
4,15		-2	-2
4,16		-1	-3
4,17
4,18
4,19
-		-	-1

Для каждой серии получаем:

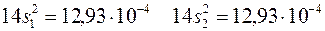
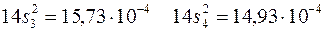
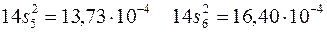
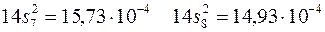
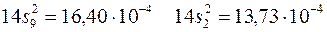
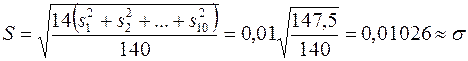
При этом оценка

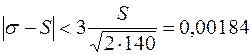
или